HM1 – Tangentengleichung bestimmen [Definition, Formel, Beispiele, Video]

Eine Tangente ist eine Gerade, die eine Funktion in genau einem Punkt berührt, ohne sie zu schneiden. An diesem Punkt hat die Tangente die gleiche Steigung wie die Funktion.

👉 Einfach gesagt: Die Tangente “streift” die Kurve, ohne sie zu schneiden.

Beispiel!

Ein Auto, das auf einer gebogenen Straße fährt, ändert ständig seine Richtung. Die Tangente zeigt an, in welche Richtung es in einem bestimmten Moment fährt.

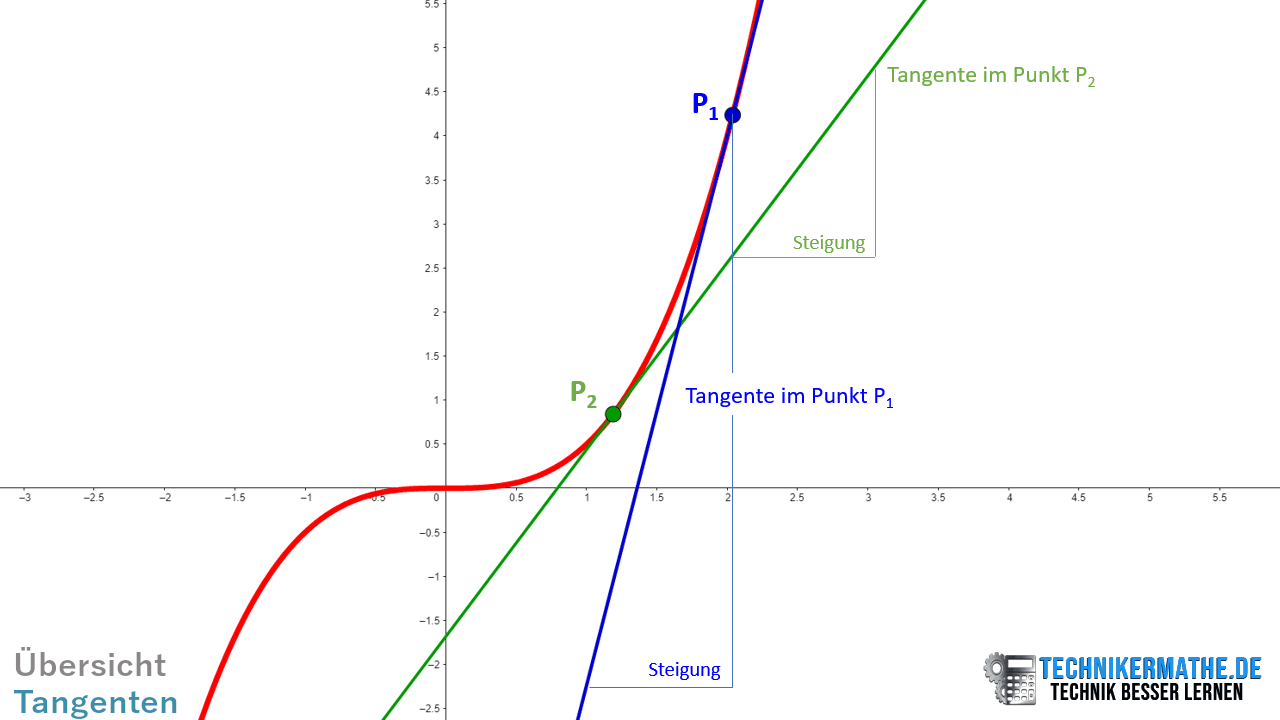
In der obigen Grafik siehst du eine kubische Funktion mit zwei beliebig ausgewählten Punkten auf der Funktion. Jeder Punkt hat eine andere Tangente und damit auch eine andere Steigung. Es sind zwei Tangenten eingezeichnet, die jeweils zu einem Punkt der Funktion gehören. Diese Tangenten zeigen die Steigung der Funktion in genau diesem Punkt an. So gehört die blaue Tangente zum Punkt P₁ und zeigt die Steigung an, die in diesem Punkt für die betrachtete Funktion gilt.

Die grüne Tangenten hingegen gehört zum Punkt P₂ und zeigt die Steigung der betrachteten Funktion in genau diesem Punkt an. Je nachdem welchen Punkt wir auf der Funktion betrachten, ändert sich auch die Steigung und damit sind die Tangenten verschieden.

In dieser Lerneinheit zeigen wir dir, wie du die Gleichung von Tangenten bestimmst.

Für ein optimales Verständnis helfen dir zwei anschauliche Rechenbeispiele und ein Lernvideo zu dem Thema.

Mehr zu diesem Thema und der höheren Mathematik findest du im Kurs: HM1 – Höhere Mathematik 1

Formel: Tangentengleichung

Wir können die Gleichung von Tangenten mit der folgenden Formel bestimmen:

Tangentengleichung aufstellen

$g(x) = f(x_0) + f'(x_0)(x - x_0)$

Hierbei ist x₀ die Stelle, für welche die Steigung gesucht wird. f(x₀) ist der Funktionswert an der Stelle x₀ und f'(x₀) ist die Steigung an der Stelle x₀.

Video: Tangentengleichung bestimmen

Tangentengleichung bestimmen – Quadratische Funktion

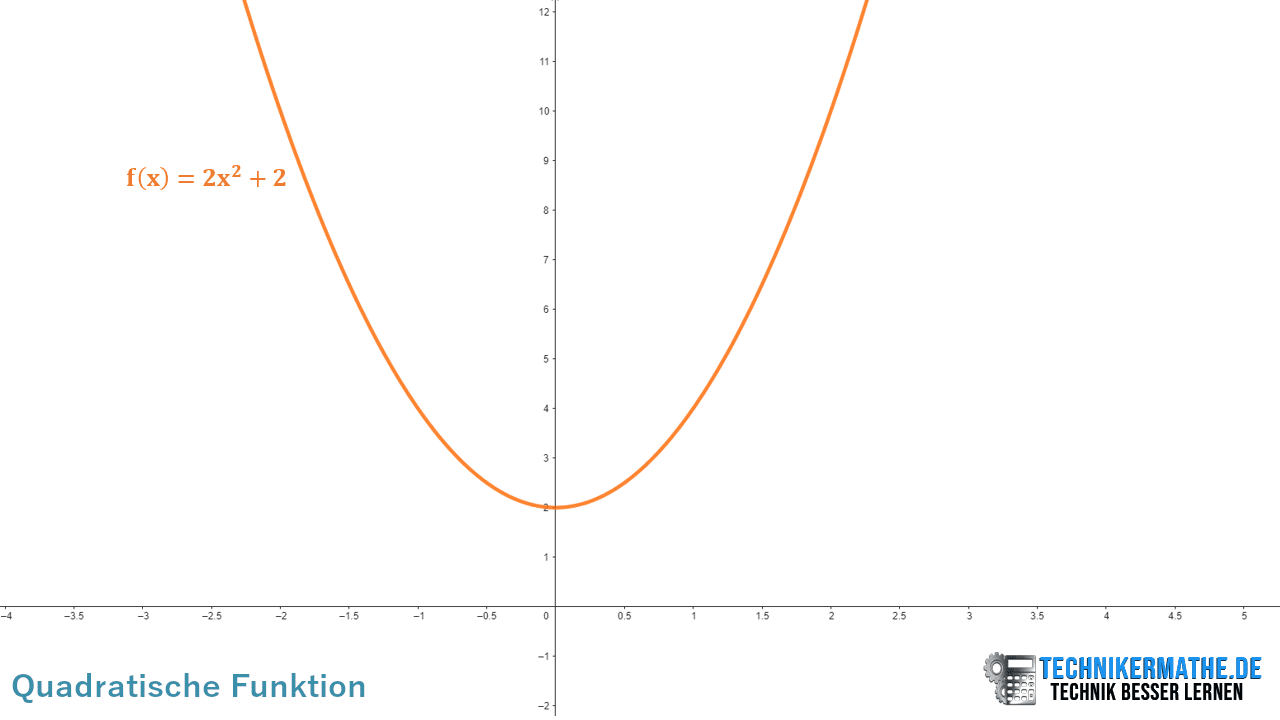
Betrachten wir die nachfolgende quadratische Funktion:

In der obigen Grafik siehst du eine quadratische Funktion (=Parabel), die nach oben geöffnet ist. Bei der Ableitung ergibt sich eine lineare Steigungsfunktion. Die Steigung ist also nicht mehr überall gleich (wie bei der linearen Funktion), sondern in jedem Punkt unterschiedlich.

Die Funktion lautet:

$f(x) = 2x^2 + 2$

Die Steigungsfunktion können wir mittels Differentialquotienten (siehe vorherige Lerneinheit) bestimmen:

$f'(x) = 4x$ Steigungsfunktion

Betrachten wir dazu zwei Beispiele.

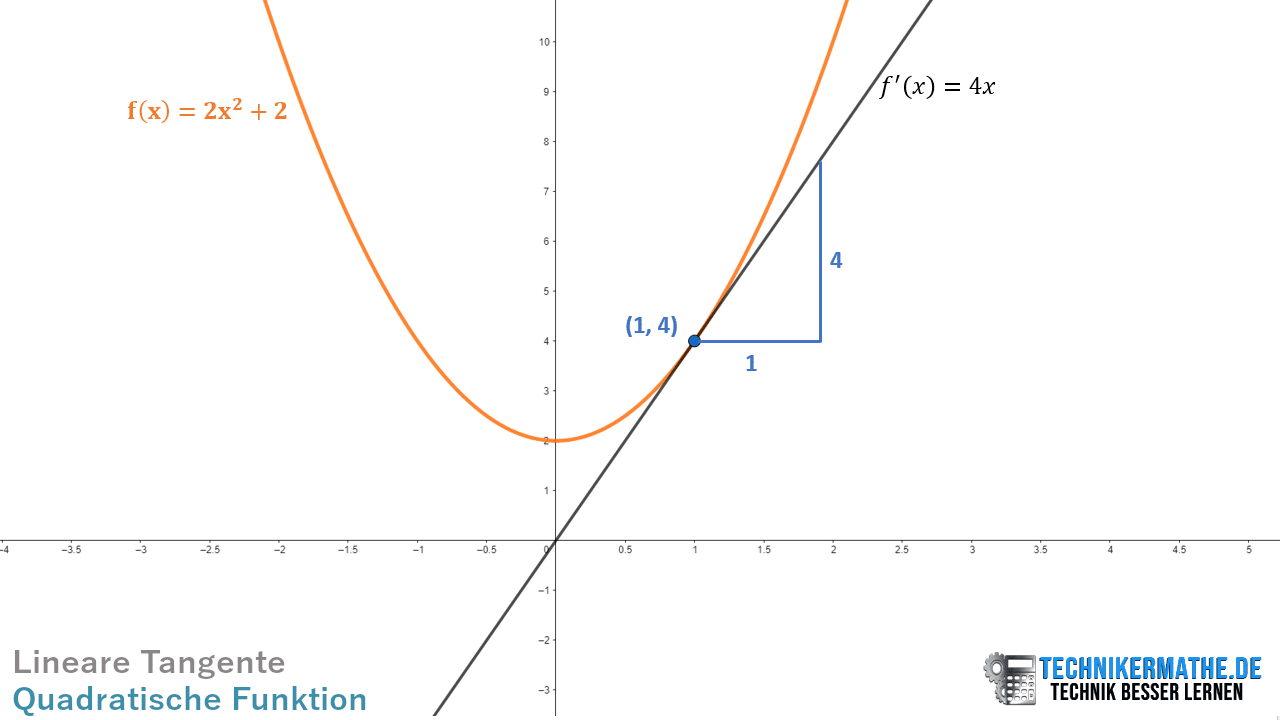
Beispiel 1: Tangentengleichung bestimmen

Beispiel!

Die Funktion lautet:

$f(x) = 2x^2 + 2$

Die Steigungsfunktion können wir mittels Differentialquotienten (siehe vorherige Lerneinheit) bestimmen:

$f'(x) = 4x$ Steigungsfunktion

Betrachten wir die Stelle $x_0 = 1$ .

Wir verwenden die obige Formel:

$g(x) = f(x_0) + f'(x_0)(x - x_0)$

Wir starten zunächst mit $f(x_0)$ :

$f(x_0 = 1) = 2 \cdot 1^2 + 2 = 4$

Als nächstes betrachten wir $f'(x_0)$

$f'(x_0 = 1) = 4 \cdot 1 = 4$

Wir können jetzt alles in die Formel einsetzen:

$g(x) = 4 + 4 \cdot (x - 1)$

$g(x) = 4 + 4x - 4$

$g(x) = 4x$ Tangentengleichung

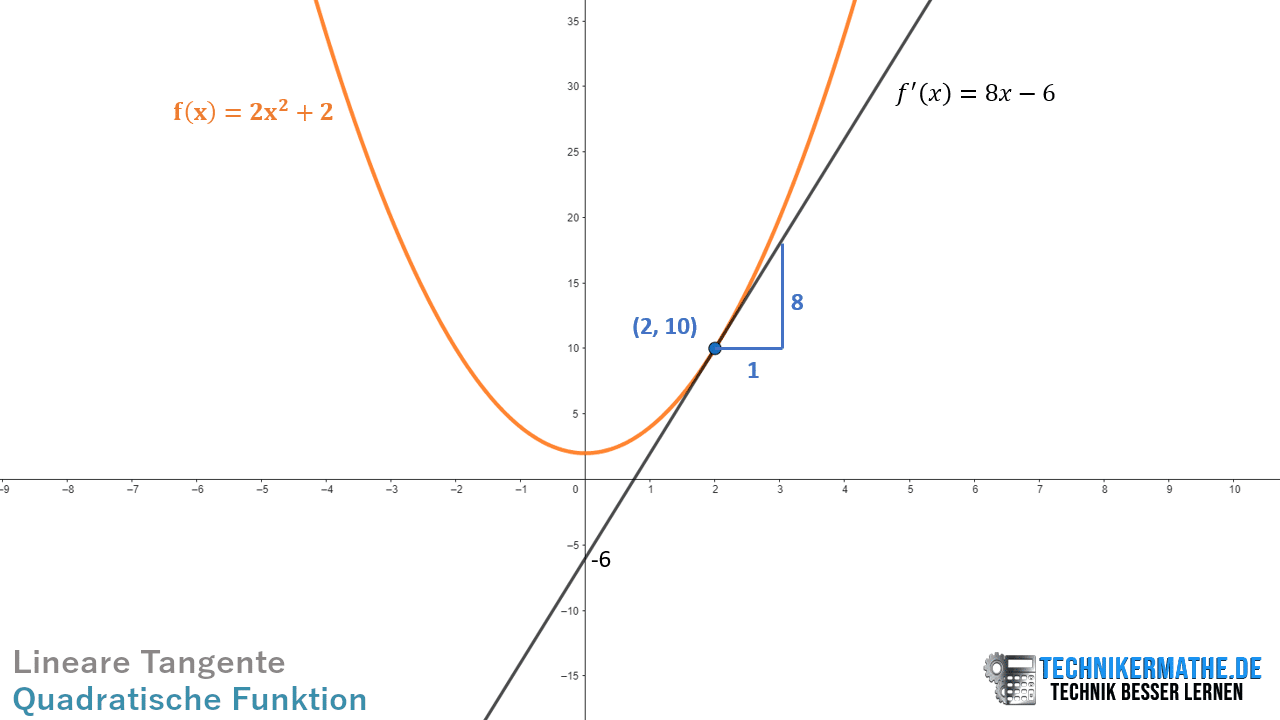
Beispiel 2: Tangentengleichung bestimmen

Beispiel!

Die Funktion lautet wieder:

$f(x) = 2x^2 + 2$

Die Steigungsfunktion können wir mittels Differentialquotienten (siehe vorherige Lerneinheit) bestimmen:

$f'(x) = 4x$ Steigungsfunktion

Betrachten wir dieses mal die Stelle $x_0 = 2$ .

Wir verwenden die obige Formel:

$g(x) = f(x_0) + f'(x_0)(x - x_0)$

Wir starten zunächst mit $f(x_0)$ :

$f(x_0 = 2) = 2 \cdot 2^2 + 2 = 10$

Als nächstes betrachten wir $f'(x_0)$

$f'(x_0 = 2) = 4 \cdot 2 = 8$

Wir können jetzt alles in die Formel einsetzen:

$g(x) = 10 + 8 \cdot (x - 2)$

$g(x) = 10 + 8x - 16$

$g(x) = 8x - 6$ Tangentengleichung

Was kommt als Nächstes?

In der folgenden Lerneinheit betrachten wir Tangentengleichungen für Funktionen höheren Grades.

FAQs zur Tangentengleichung

1. Was ist die Tangentengleichung?

Die Tangentengleichung beschreibt eine Gerade, die eine Funktion in genau einem Punkt berührt. Sie hat die allgemeine Form:

$f'(x_0) \cdot (x - x_0) + f(x_0)$

Dabei ist $f'(x_0)$ die Steigung der Funktion am Berührungspunkt $x_0$ .

2. Wie finde ich die Steigung der Tangente?

Die Steigung ist die Ableitung $f'(x)$ der Funktion, ausgewertet am Berührungspunkt $x_0$ .

Beispiel: Für $f(x) = x^2$ ist die Ableitung $f'(x) = 2x$ . Am Punkt $x_0 = 1$ beträgt die Steigung $f'(1) = 2 \cdot 1 = 2$ .

3. Was brauche ich, um die Tangentengleichung zu bestimmen?

Du benötigst:

Die Funktion $f(x)$ .
Die Ableitung $f'(x)$ .
Den Berührungspunkt $P(x_0, f(x_0))$ .

4. Kann es mehrere Tangenten an einer Funktion geben?

Ja, an verschiedenen Punkten der Funktion gibt es jeweils eine Tangente mit einer spezifischen Steigung. Es gibt auch Spezialfälle, z. B. wenn die Funktion symmetrisch ist oder mehrere Berührungspunkte mit derselben Tangente hat.

5. Wie unterscheidet sich Tangenten von Sekanten?

Tangenten berühren die Funktion in genau einem Punkt und hat dort dieselbe Steigung wie die Funktion.
Sekanten schneidet die Funktion in zwei oder mehr Punkten und beschreibt keine lokale Steigung.

Lerne jetzt mit uns!

Wir von Technikermathe.de bieten dir leicht verständliche Erklärungen, Übungsaufgaben und Schritt-für-Schritt-Lösungen rund um das Thema Tangenten. In unseren Kursen findest du:
✅ Videos, die dich Schritt für Schritt begleiten.
✅ Interaktive Übungen, um dein Wissen zu festigen.
✅ Beispiele, die sich direkt auf Prüfungsaufgaben beziehen.

Starte jetzt und meistere Tangenten wie ein Profi!

👨‍🏫 Jetzt Tangentenkurs starten
📘 Mehr über unsere Kurse erfahren

Dein Mathe-Erfolg beginnt hier! 😊

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich, Binomialkoeffizient, n über k

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++