HM1 – Satz vom Minimum und Maximum (Weierstraß) – Einfach erklärt

Definition

Der Satz von Weierstraß besagt, dass jede stetige Funktion, die auf einem kompakten Intervall [a, b] definiert ist, ein globales Minimum und ein globales Maximum annimmt. Das bedeutet, dass es innerhalb des Intervalls Punkte gibt, an denen die Funktion ihre kleinsten und größten Werte erreicht.

In dieser Lerneinheit behandeln wir den Satz vom Minimum und Maximum der auch als Satz von Weierstraß bekannt ist.

Für ein optimales Verständnis helfen dir drei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der höheren Mathematik findest du im Kurs: HM1 – Höhere Mathematik 1

Bedingungen des Satzes

Stetigkeit: Die Funktion muss stetig sein, d. h. sie darf keine Sprünge oder Unstetigkeitsstellen haben.
Kompaktes Intervall: Das Intervall $[a, b]$ muss ein kompaktes Intervall sein, das bedeutet:
- Es ist abgeschlossen (es enthält die Endpunkte und ).
- Es ist beschränkt (die Funktionswerte sind innerhalb eines bestimmten Bereichs).

Auf einem kompakten Intervall ist jede stetige Funktion nach dem Weierstraßschen Extremwertsatz garantiert beschränkt und erreicht tatsächlich ihr Maximum und Minimum.

Bezug zu Extremwerten

Die Extremwerte einer Funktion sind die Punkte, an denen die Funktion entweder ein Maximum oder ein Minimum erreicht. Der Satz von Weierstraß stellt sicher, dass auf einem kompakten Intervall stets globale Extremwerte existieren, falls die Funktion stetig ist.

Lokale Extremwerte: Diese treten auf, wenn die Funktion innerhalb eines kleinen Bereichs (lokal) den höchsten oder niedrigsten Wert hat.
Globale Extremwerte: Diese beziehen sich auf den höchsten oder niedrigsten Wert der Funktion im gesamten betrachteten Intervall.

Die Extremwertsuche in der Praxis basiert oft auf der Berechnung der Ableitungen (z. B. bei der Differentiation) und der Untersuchung kritischer Punkte. Der Satz von Weierstraß gibt jedoch zusätzlich die Garantie, dass globale Extremwerte existieren, ohne dass Ableitungen betrachtet werden müssen.

Satz von Weierstraß: Formel

Sei $f: [a, b] \to \mathbb{R}$ eine stetige Funktion. Dann existieren Punkte $x_{\text{min}}, x_{\text{max}} \in [a, b]$ , sodass gilt:

Satz von Weierstraß

$f(x_{\text{min}}) \leq f(x) \leq f(x_{\text{max}}) \quad \text{für alle } x \in [a, b]$

Um die Extremwerte einer Funktion genauer zu bestimmen, können kritische Punkte über die Ableitungen identifiziert werden. Kritische Punkte sind die Stellen, an denen die erste Ableitung $f'(x)$ entweder null ist oder nicht definiert ist. Mithilfe des Satzes von Weierstraß können wir sicher sein, dass diese Extremwerte im betrachteten Intervall tatsächlich existieren, wenn die Funktion stetig ist.

Wichtige Hinweise

Der Satz garantiert nur, dass Extremwerte existieren, aber nicht, wie man sie findet. Um das Minimum und Maximum zu bestimmen, sucht man typischerweise nach kritischen Punkten (wo die erste Ableitung null ist oder nicht definiert ist) und überprüft dann die Randwerte des Intervalls.
Kritische Punkte und Randpunkte müssen zusammen betrachtet werden, wenn man nach Extremwerten sucht. Ein lokales Extremum (Minimum oder Maximum) kann auch ein globales Extremum auf einem kompakten Intervall sein, wenn es die größte bzw. kleinste Funktion hat.

Anwendung und Bedeutung

Der Satz vom Minimum und Maximum ist besonders nützlich in der Mathematik und Physik, da er garantiert, dass eine stetige Funktion auf einem kompakten Intervall immer Extremwerte erreicht. Dies wird zum Beispiel bei der Suche nach optimalen Lösungen in Optimierungsproblemen verwendet.

Ein klassisches Beispiel ist die Bestimmung des maximalen oder minimalen Wertes einer Funktion, die physikalische Größen wie Temperatur oder Druck beschreibt, innerhalb eines gegebenen Intervalls.

Möglichkeit zur Bestimmung der globalen Extremwerte

Funktion ableiten und kritische Punkte bestimmen (wo f'(x) = 0 oder f'(x) nicht definiert ist).
Funktionswerte an den kritischen Punkten und den Intervallgrenzen berechnen.
Vergleich der Funktionswerte: Der kleinste Wert ist das globale Minimum, der größte Wert das globale Maximum.

Das Einsetzen an den Intervallgrenzen ist notwendig, da globale Extremwerte oft dort auftreten können, insbesondere wenn es keine kritischen Punkte innerhalb des Intervalls gibt.

Zum besseren Verständnis betrachten wir nachfolgend zwei ausführliche Beispiele.

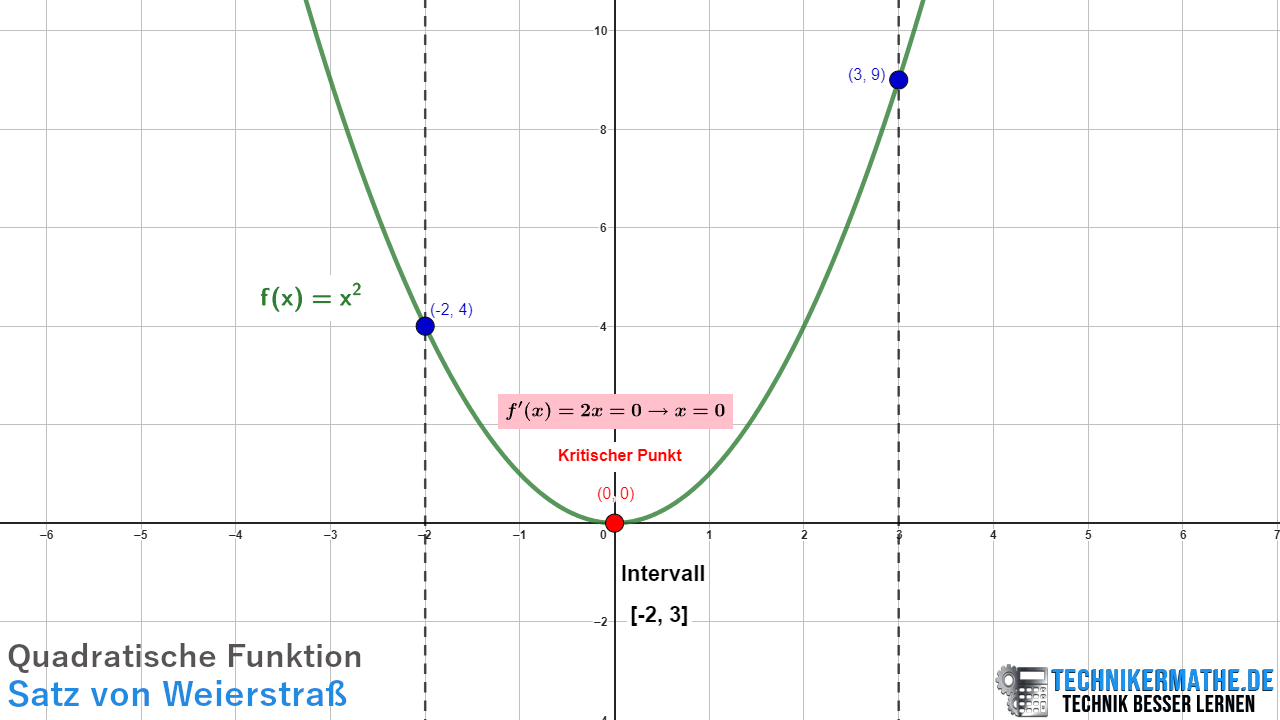
Beispiel 1: Quadratische Funktion

Aufgabenstellung

Betrachten wir die folgende Funktion:

$f(x) = x^2$ auf dem Intervall $[-2, 3]$ .

Kritische Punkte ermitteln

Die Ableitung lautet: $f'(x) = 2x$

Setze $f'(x) = 0$ , um die kritischen Punkte zu finden:

$2x = 0 \implies x = 0$

Der kritische Punkt $x = 0$ liegt im Intervall $[-2, 3]$ .

Funktionswerte an den Intervallgrenzen und dem kritischen Punkt:

$f(-2) = (-2)^2 = 4$

$f(0) = 0^2 = 0$

$f(3) = 3^2 = 9$

Globales Minimum und Maximum bestimmen:

Das kleinste $f(x)$ ist $f(0) = 0$ (globales Minimum).

Das größte $f(x)$ ist $f(3) = 9$ (globales Maximum).

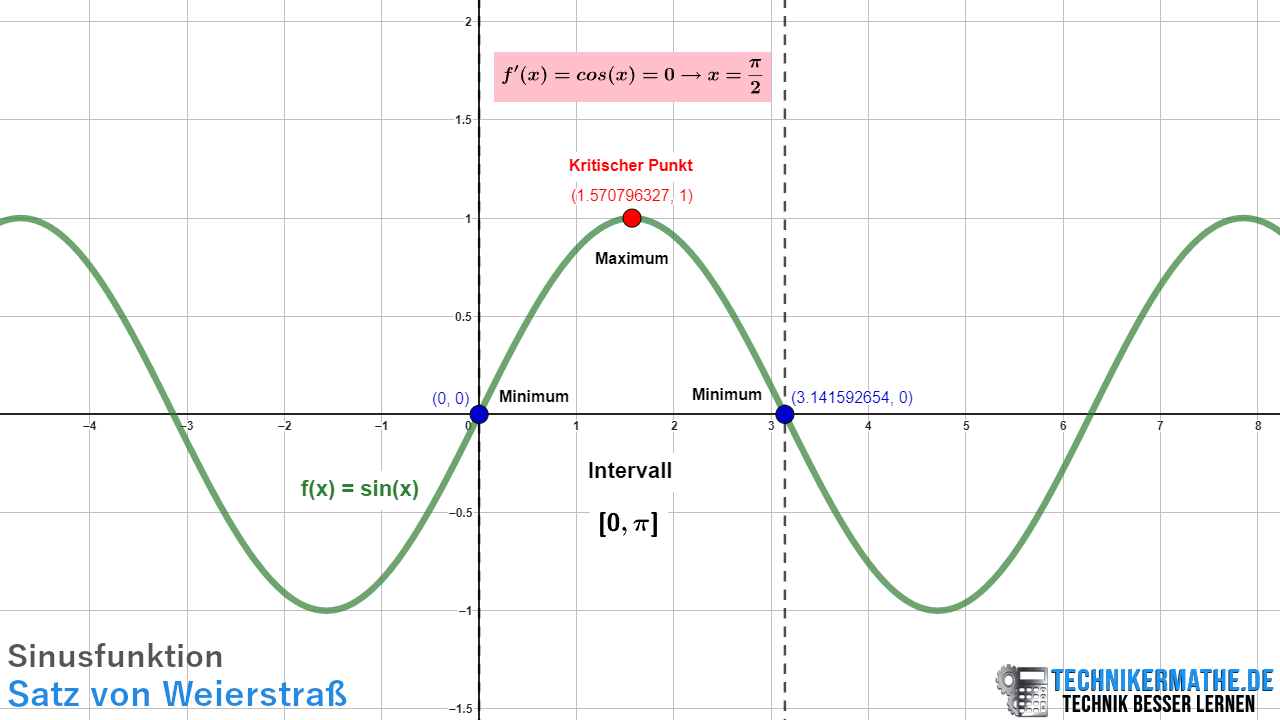
Beispiel 2: Trigonometrische Funktion

Aufgabenstellung

Betrachten wir die folgende Funktion:

$f(x) = \sin(x)$ auf dem Intervall $[0, \pi]$ .

Kritische Punkte ermitteln

Die Ableitung lautet: $f'(x) = \cos(x)$

Setze $f'(x) = 0$ , um die kritischen Punkte zu finden:

$\cos(x) = 0 \implies x = \frac{\pi}{2}$

Der kritische Punkt $x = \frac{\pi}{2}$ liegt im Intervall $[0, \pi]$ .

Funktionswerte an den Intervallgrenzen und dem kritischen Punkt:

$f(0) = \sin(0) = 0$

$f\left(\frac{\pi}{2}\right) = \sin\left(\frac{\pi}{2}\right) = 1$

$f(\pi) = \sin(\pi) = 0$

Globales Minimum und Maximum bestimmen:

Das kleinste $f(x)$ ist $f(0) = 0$ oder $f(\pi) = 0$ (globales Minimum).

Das größte $f(x)$ ist $f\left(\frac{\pi}{2}\right) = 1$ (globales Maximum).

Zusammenfassung:

Der Satz vom Minimum und Maximum garantiert für stetige Funktionen auf kompakten Intervallen, dass ein globales Minimum und Maximum existieren.
Wichtige Voraussetzungen: Stetigkeit der Funktion und ein kompaktes Intervall.
Der Satz ist besonders wichtig in der Optimierung, bei der Suche nach maximalen oder minimalen Werten einer Funktion auf einem geschlossenen und beschränkten Bereich.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich, Binomialkoeffizient, n über k

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++