HM1 – Konkave und konvexe Funktion – Einfach erklärt

Eine Funktion ist konvex, wenn die Verbindungslinie zwischen zwei Punkten auf dem Graphen immer oberhalb oder auf dem Graphen liegt, und konkav, wenn sie immer unterhalb oder auf dem Graphen liegt.

In dieser Lerneinheit betrachten wir konvexe und konkave Funktionen. Wir zeigen dir, was der Unterschied zwischen konvexen und konkaven Funktionen ist.

Für ein optimales Verständnis helfen dir drei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der höheren Mathematik findest du im Kurs: HM1 – Höhere Mathematik 1

Konkave und konvexe Funktion in der Differentialrechnung

Konvexe und konkave Funktionen gehören zur Differentialrechnung, weil ihre Eigenschaften eng mit der Ableitung der Funktion zusammenhängen:

Konvexe Funktionen: Eine Funktion ist konvex, wenn ihre Ableitung (oder die zweite Ableitung) in einem Intervall nicht abnimmt. Das bedeutet, dass die Steigung der Funktion immer gleich bleibt oder zunimmt, was in der Differentialrechnung durch die Untersuchung der ersten und zweiten Ableitung analysiert wird.
Konkave Funktionen: Eine Funktion ist konkav, wenn ihre Ableitung (oder die zweite Ableitung) in einem Intervall nicht zunimmt, also die Steigung immer gleich bleibt oder abnimmt. Auch diese Eigenschaft wird durch die Analyse der Ableitungen untersucht.

In der Differentialrechnung wird also durch die Untersuchung der Ableitungen und der Krümmung (zweite Ableitung) erkannt, ob eine Funktion konvex oder konkav ist, was wichtige Schlussfolgerungen für Optimierung und Analyse ermöglicht.

Eine Funktion ist konvex, wenn ihre Graphenform so aussieht, dass jede Verbindungslinie zwischen zwei Punkten auf dem Graphen immer oberhalb oder genau auf dem Graphen liegt:

Konvexe Funktion, konvex, Beispiel, Definition, Beschreibung, konkave und konvexe Funktion, Verbindungslinie, unterhalb — Konvexe Funktion

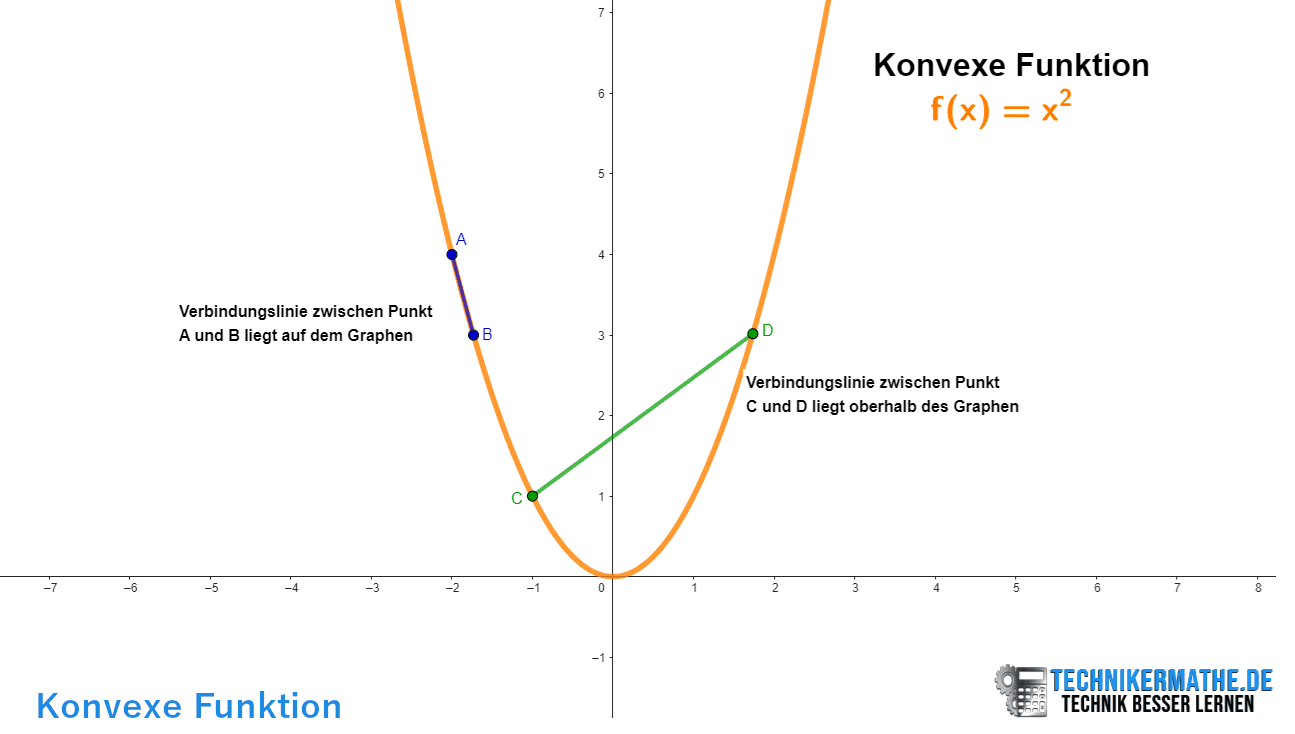
Eine Funktion ist konkav, wenn ihre Graphenform so ist, dass jede Verbindungslinie zwischen zwei Punkten auf dem Graphen immer unterhalb oder genau auf dem Graphen liegt:

Konkave Funktion, Definition, Beispiel, Beschreibung, Verbindungslinie — Konkave Funktion

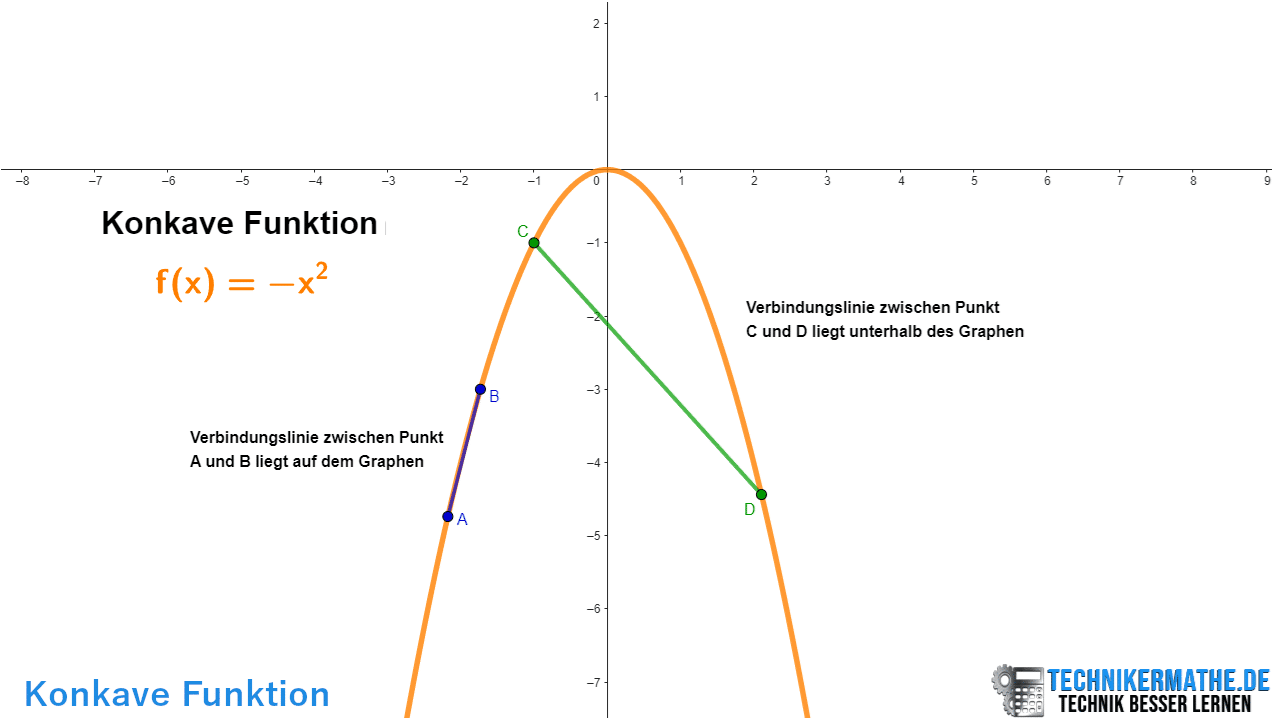
Die Definitionen von konvexen und konkaven Funktionen können auf zwei Arten formuliert werden, die auf der Geometrie der Funktion basieren:

Über die Verbindungslinie von zwei Punkten:

Konvex: Eine Funktion ist konvex, wenn die Verbindungslinie zwischen zwei beliebigen Punkten auf dem Graphen der Funktion immer oberhalb oder genau auf dem Graphen liegt.
Konkav: Eine Funktion ist konkav, wenn die Verbindungslinie zwischen zwei beliebigen Punkten auf dem Graphen immer unterhalb oder genau auf dem Graphen liegt.

Über die Tangente:

Konvex: Eine Funktion ist konvex, wenn der Graph immer oberhalb der Tangente an jedem Punkt liegt, d.h. die Funktion “nach oben öffnet”.
Konkav: Eine Funktion ist konkav, wenn der Graph immer unterhalb der Tangente an jedem Punkt liegt, d.h. die Funktion “nach unten öffnet”.

Beide Ansätze (Verbindungslinie und Tangente) führen zu denselben Eigenschaften und können je nach Kontext verwendet werden, um die Konvexität oder Konkavität einer Funktion zu charakterisieren.

Definition: Konvexe Funktion

Eine Funktion $f(x)$ ist konvex, wenn die folgende Bedingung erfüllt ist:

Konvexe Funktion

Eine Funktion $f(x)$ ist konvex in einem Intervall, wenn für jeden Punkt $x_0$ im Intervall die Tangente an $f(x)$ unterhalb des Graphen liegt:

$f(x) \geq f(x_0) + f'(x_0)(x - x_0), \quad \forall x \in \text{Intervall}$

In Worten: Der Funktionswert f(x) ist für alle x im betrachteten Intervall immer größer oder gleich dem Wert der Tangente an der Funktion f(x)an der Stelle x₀.

Oder anders formuliert: Die Funktion f(x) liegt im Intervall niemals unterhalb der Tangente, die an der Stelle x₀ an die Funktion gelegt wurde.

Die zweite Ableitung $f''(x)$ gibt Auskunft über die Krümmung der Funktion:

Konvexe Funktionen: $f''(x) > 0$ → Der Graph ist nach oben gekrümmt, und die Tangente liegt unterhalb.
Beispiele: $x^2$ , $e^x$ .

Definition: Konkave Funktion

Eine Funktion $f(x)$ ist konkav, wenn die folgende Bedingung erfüllt ist:

Konkave Funktion

Eine Funktion $f(x)$ ist konkav in einem Intervall, wenn für jeden Punkt $x_0$ im Intervall die Tangente an $f(x)$ oberhalb des Graphen liegt:

$f(x) \leq f(x_0) + f'(x_0)(x - x_0), \quad \forall x \in \text{Intervall}$

In Worten: Der Funktionswert f(x) ist für alle x im betrachteten Intervall immer kleiner oder gleich dem Wert der Tangente an der Funktion f(x) an der Stelle x₀.

Oder anders formuliert: Die Funktion f(x) liegt im Intervall niemals oberhalb der Tangente, die an der Stelle x₀ an die Funktion gelegt wurde.

Die zweite Ableitung $f''(x)$ gibt Auskunft über die Krümmung der Funktion:

Konkave Funktionen: $f''(x) < 0$ → Der Graph ist nach unten gekrümmt, und die Tangente liegt oberhalb.
Beispiele: $\ln(x)$ , $-x^2$ .

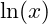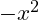Der Übergang zwischen konvex und konkav wird durch Wendepunkte bestimmt, falls diese existieren.

Beispiel 1: Quadratische Funktion

Aufgabenstellung

Gegeben sei die folgende Funktion:

$f(x) = x^2$

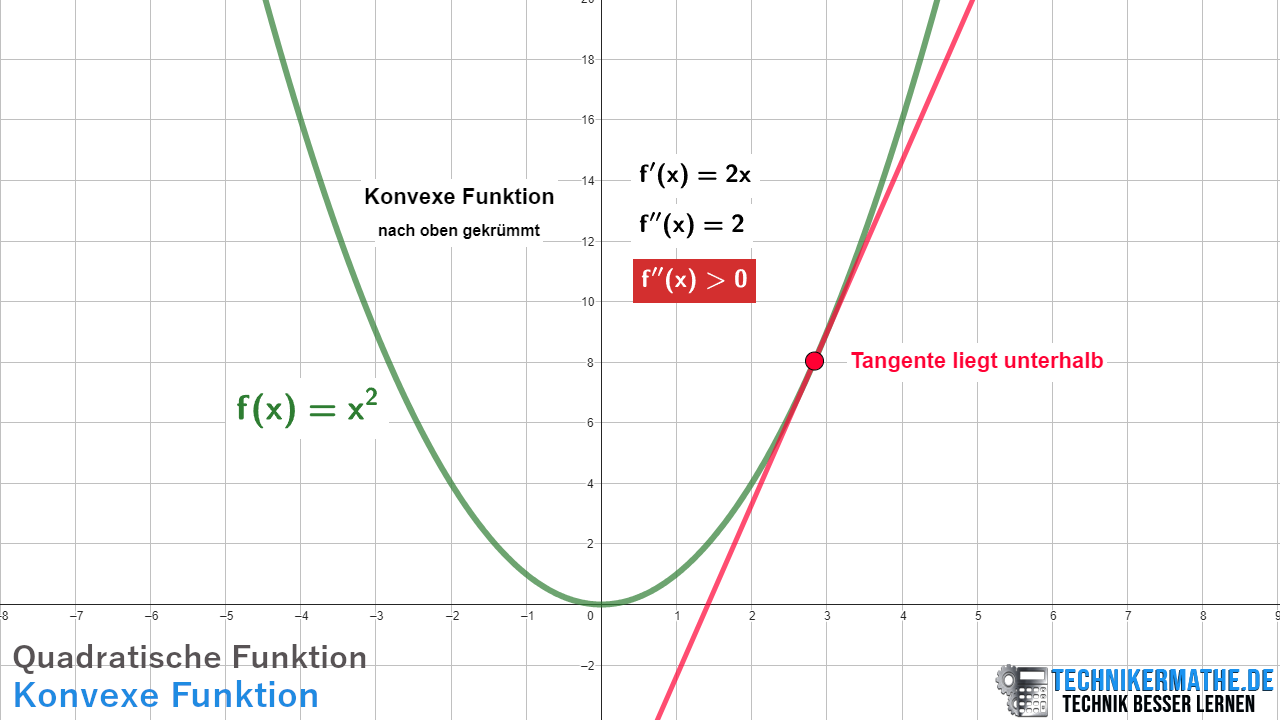
Bestimme, ob die Funktion konkav oder konvex ist.

Erste Ableitung: $f'(x) = 2x$

Zweite Ableitung: $f''(x) = 2$

Da $f''(x) = 2 > 0$ für alle x, ist $f(x) = x^2$ eine konvexe Funktion.

Graph: Der Graph von $f(x) = x^2$ ist eine nach oben geöffnete Parabel.

Konvexe Funktion, quadratische Funktion, nach oben geöffnet, Tangente — Beispiel: Konvexe Funktion – Quadratische Funktion

Beispiel 2: Natürlicher Logarithmus

Aufgabenstellung

Gegeben sei die folgende Funktion:

$f(x) = \ln(x)$

Bestimme, ob die Funktion konkav oder konvex ist.

Erste Ableitung: $f'(x) = \frac{1}{x}$

Zweite Ableitung: $f''(x) = -\frac{1}{x^2}$

Da $f''(x) = -\frac{1}{x^2} < 0$ für $x > 0$ , ist $f(x) = \ln(x)$ eine konkave Funktion.

Graph: Der Graph von $f(x) = \ln(x)$ steigt, aber flacht immer mehr ab (nach unten gekrümmt).

Konkave Funktion, Logarithmus, nach unten gekrümmt, Tangente — Beispiel: konkave Funktion – Logarithmus

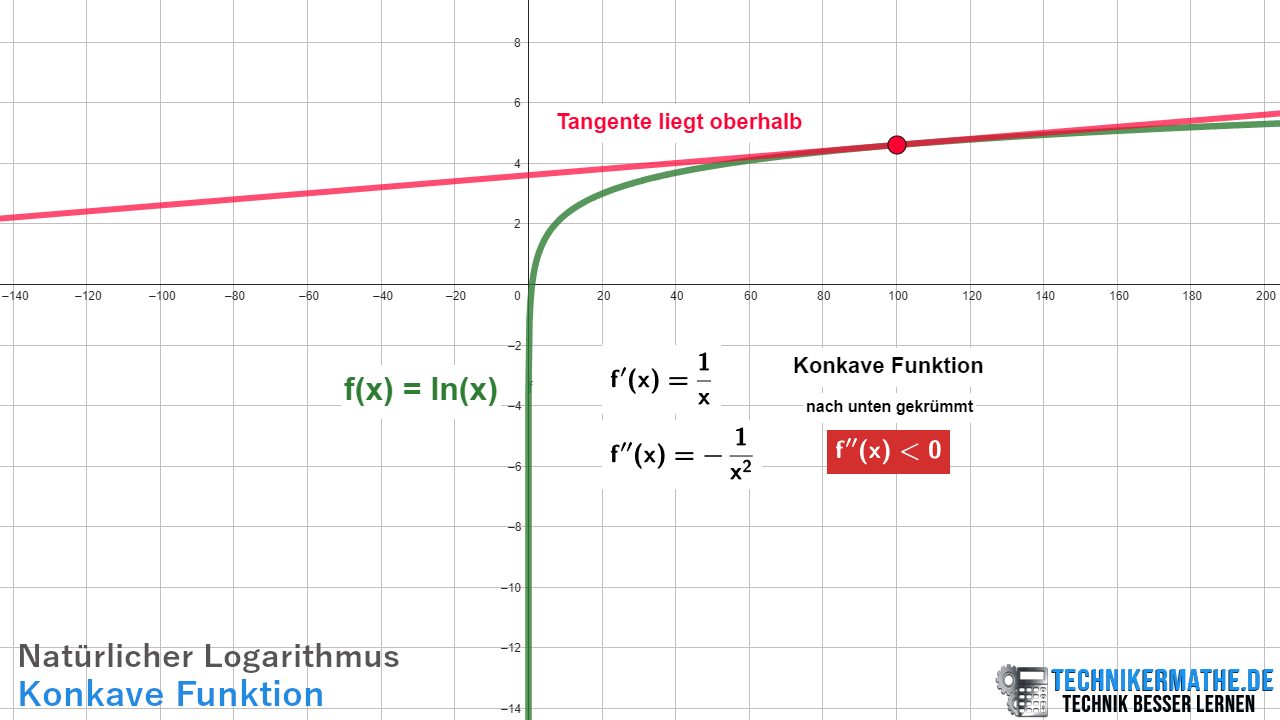
In der obigen Grafik sehen wir einen Teil der Funktion f(x) = ln(x). Diese Funktion ist eine konkave Funktion, da die zweite Ableitung kleiner als Null ist. Wir sehen, dass die Tangente eines Punktes oberhalb der Funktion liegt.

Beispiel 3: Logarithmus und quadratische Funktion

Aufgabenstellung

Betrachten wir die folgende Funktion:

$f(x) = \ln(x^2)$

Wir analysieren ihre Konvexität oder Konkavität.

Schritt 1: Definitionsbereich

Die Funktion $\ln(x^2)$ ist definiert, wenn $x^2 > 0$ , also $x \neq 0$ .

Der Definitionsbereich lautet:

$D_f = \mathbb{R} \setminus \{0\}$

In Worten: Der Definitionsbereich der gegebenen Funktion umfasst alle reellen Zahlen außer Null.

Schritt 2: Erste Ableitung

Wir haben hier eine zusammengesetzte Funktion gegeben. Um diese Funktion abzuleiten wenden wir die Kettenregel an. Der Logarithmus ist die äußere Funktion und die quadratische Funktion die innere Funktion.

Äußere Funktion: $h(g) = \ln(g)$ mit $g = x^2$ als Konstante

Innere Funktion: $g(x) = x^2$

Wir leiten beide Funktionen ab:

Äußere Ableitung: 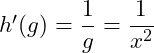$h'(g) = \dfrac{1}{g} = \dfrac{1}{x^2}$

Innere Ableitung: $g'(x) = 2x$

Zur Bestimmung der gesamten Ableitung multiplizieren wir die äußere und innere Ableitung miteinander:

$f'(x) = \dfrac{1}{x^2} \cdot 2x = \dfrac{2x}{x^2} = \dfrac{2}{x}$

Schritt 3: Zweite Ableitung

Für die zweite Ableitung benötigen wir nicht mehr die Kettenregel. Wir können hier wie folgt ableiten:

$f'(x) = \dfrac{2}{x} = 2 \cdot x^{-1}$

$f''(x) = (-1) \cdot 2 \cdot x^{-1-1} = -2 \cdot x^{-2} = -\frac{2}{x^2}$

Schritt 4: Analyse der zweiten Ableitung

Für $x>0$ gilt $f''(x) = -\frac{2}{x^2} < 0$

Für $x < 0$ gilt ebenfalls $f''(x) = -\frac{2}{x^2} < 0$

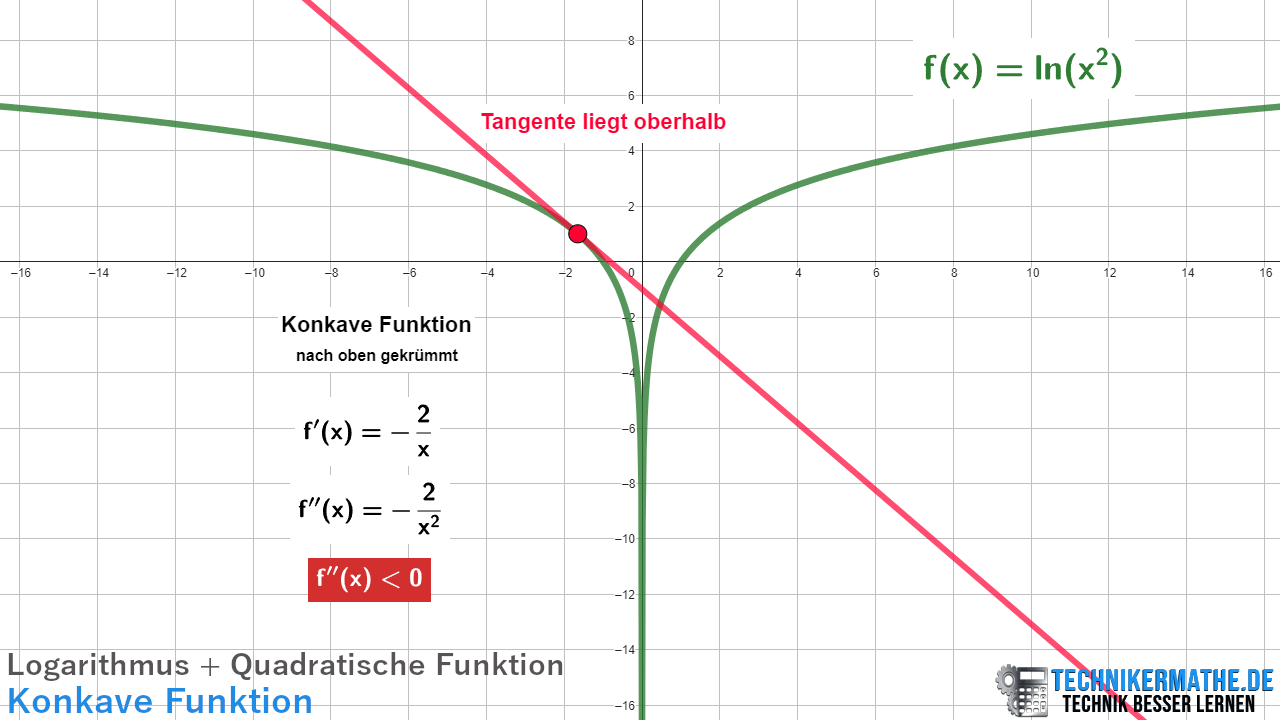
Setzt du negative Werte für x² ein, so resultieret ein positiver Wert. Damit wird der Funktionswert negativ, aufgrund des Minuszeichens vor dem Bruch.

Da die zweite Ableitung auf dem gesamten Definitionsbereich negativ ist, ist $f(x) = \ln(x^2)$ konkav (nach oben gekrümmt).

Konkave Funktion, Logarithmus, Kettenregel, nach oben geöffnet, Konkavität, Tangente — Beispiel: Konkave Funktion – Zusammengesetzte Funktion

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich, Binomialkoeffizient, n über k

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++