TM2 – Gesamtdehnung im Stab [Formel, Beispiel, Video]

Wir betrachten in dieser Lerneinheit ein Beispiel zur Berechnung der Gesamtdehnung eines Stabes infolge äußerer Einwirkungen. Die Dehnung oder Stauchung eines Stabs kann unterschiedliche Ursachen haben.

In dieser Lerneinheit wollen wir uns anschauen, wie die Gesamtdehnung im Stab berechnet wird.

Für ein optimales Verständnis helfen dir ein ausführliches Video und ein anschauliches Rechenbeispiel zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Ursachen: Dehnung im Stab

Die Dehnung eines Stabs kann verschiedene Ursachen haben, die häufig in folgende Kategorien eingeteilt werden können:

Mechanische Belastung: Die offensichtlichste Ursache für die Dehnung eines Stabs ist die Anwendung einer mechanischen Belastung, sei es durch Zug, Druck oder Biegung. Eine Zugbelastung führt zu einer positiven Dehnung, während eine Druckbelastung zu einer negativen Dehnung (=Stauchung) führen kann. Biegung kann eine Kombination aus Zug und Druck verursachen, abhängig von der Art der Biegebelastung.
Thermische Ausdehnung: Änderungen der Temperatur können ebenfalls zu einer Dehnung oder Kontraktion eines Stabs führen. Die meisten Materialien dehnen sich bei Erwärmung aus und ziehen sich bei Abkühlung zusammen. Diese thermische Ausdehnung oder Kontraktion kann signifikant sein, insbesondere bei Materialien mit hohem Ausdehnungskoeffizienten.
Chemische Reaktionen: In einigen Fällen können chemische Reaktionen zu einer Veränderung der Länge eines Stabs führen. Dies kann beispielsweise auftreten, wenn ein Metall mit einem anderen Material reagiert und dabei eine neue Verbindung bildet, die eine andere Kristallstruktur aufweist und somit eine Veränderung der Länge des Stabs bewirkt.
Kriechen: Kriechen ist die langsame Verformung eines Materials unter konstanter Belastung über einen längeren Zeitraum. Diese Deformation kann ebenfalls zu einer Dehnung des Stabs führen, insbesondere bei hohen Temperaturen und hohen Belastungen.
Materialermüdung: Bei zyklischer Belastung kann Materialermüdung auftreten, was zu einer fortschreitenden Veränderung der Länge des Stabs führen kann. Dies ist besonders relevant bei wiederholten Lastzyklen nahe der Materialgrenze oder bei ungünstigen Bedingungen wie Vibrationen oder hohen Temperaturen.

Schauen wir uns mal an, wie die Gesamtdehnung in einem Stab berechnet werden kann, wenn wir als Ursache eine Zug- bzw. Druckbelastung sowie eine Temperaturänderung berücksichtigen.

Gesamtdehnung im Stab: Formel

Die Gesamtdehnung setzt sich zusammen aus der Wärmedehnung infolge einer gegebenen Temperaturdifferenz $\triangle T$ und einer mechanischen Dehnung, infolge einer Zug- oder Druckkraft. Treten beide Fälle auf, so müssen wir beide Dehnungen bei der Berechnung der Gesamtdehnung des Stabs berücksichtigen.

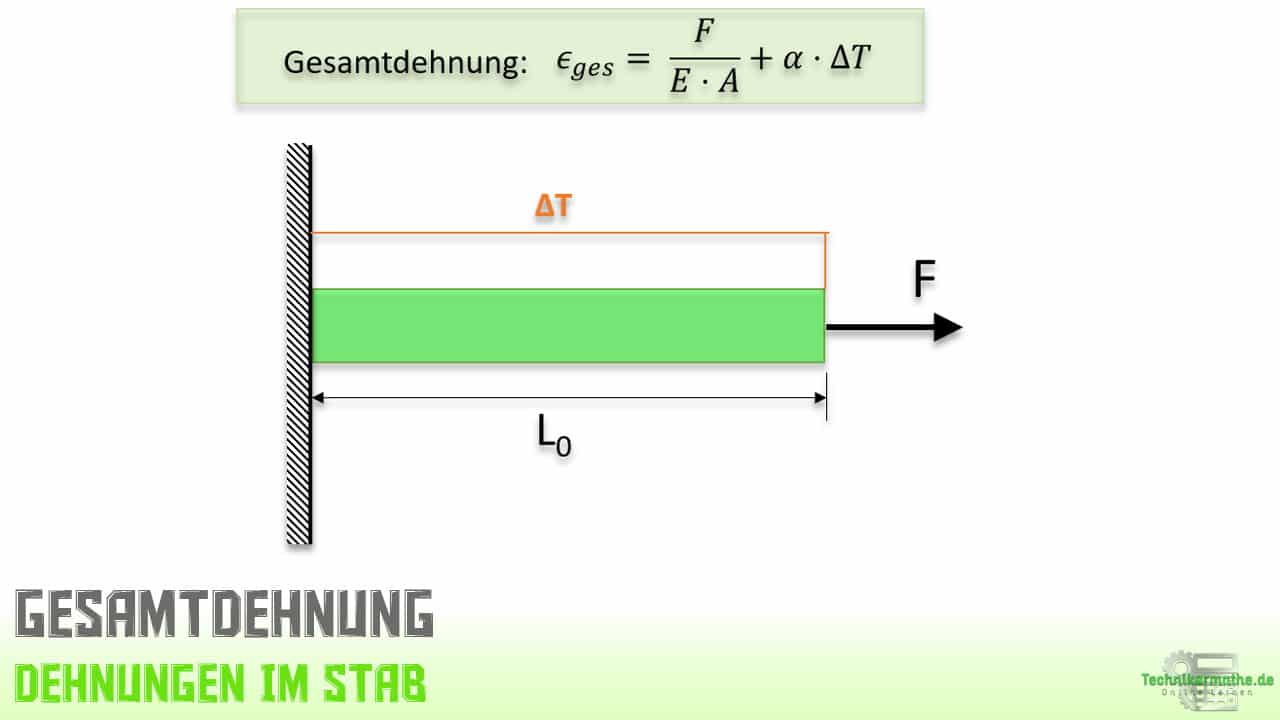
Gesamtdehnung, Wärmedehnung, Dehnung, Dehnungen im Stab, Zugkraft, Temperaturdifferenz, Temperaturänderung — Formel: Gesamtdehnung im Stab

Die Gesamtdehnung im Stab ergibt sich aus der Dehnung infolge einer Zugkraft und der Dehnung infolge einer Temperaturdifferenz:

(1) $\epsilon_{ges} = \epsilon + \epsilon_T$ Gesamtdehnung

Für die Dehnung infolge einer Zugkraft (im Weiteren mit ε_mech bezeichnet) können wir das Hookesche Gesetz heranziehen und nach der Dehnung auflösen:

$\sigma = E \cdot \epsilon_{mech}$

$\epsilon_{mech} = \dfrac{\sigma}{E}$

Für die Dehnung infolge der Temperaturdifferenz haben wir im Abschnitt Wärmedehnungen die folgende Gleichung aufgezeigt:

$\epsilon_T = \alpha \cdot \triangle T$

Wir setzen nun die einzelnen Dehnungen in die Gleichung für die Gesamtdehnung ein und erhalten:

(2) $\epsilon_{ges} = \dfrac{\sigma}{E} + \alpha \cdot \triangle T$ Gesamtdehnung

Die Normalspannung σ können wir auch bestimmen zu:

$\sigma = \dfrac{N}{A} = \dfrac{F}{A}$ Zugstab

Einsetzen führt uns auf:

(3) $\epsilon_{ges} = \dfrac{F}{EA} + \alpha \cdot \triangle T$ Gesamtdehnung

Hierbei ist F die äußere Zugkraft, E der Elastizitätsmodul, A der Querschnitt, α der Längenausdehnungskoeffizient undΔT die Temperaturdifferenz. Der gesamte Ausdruck EA wird auch als Dehnsteifigkeit bezeichnet.

Die obigen Gleichungen gelten für eine Ausdehnung des Stabs (Zugstab und Temperaturerhöhung). Ist zum Beispiel eine Druckkraft gegeben so wird die Kraft F negativ und damit folgt eine Stauchung und keine Ausdehnung. Der erste Term wird dann negativ:

$\epsilon_{ges} = -\dfrac{F}{EA} + \alpha \cdot \triangle T$ Gesamtdehnung bei Druckkraft & Temperaturerhöhung

Verringert sich die Temperatur des Stabes und zieht dieser sich zusammen, so muss der zweite Term negativ berücksichtigt werden:

$\epsilon_{ges} = \dfrac{F}{EA} - \alpha \cdot \triangle T$ Gesamtdehnung bei Zugstab und Temperaturabfall

$\epsilon_{ges} = -\dfrac{F}{EA} - \alpha \cdot \triangle T$ Gesamtdehnung bei Druckstab und Temperaturabfall

Video: Gesamtdehnung im Stab berechnen

Im folgenden Video zeigen wir dir anhand eines Beispiels, wie du die Gesamtdehnung in einem Stab berechnen kannst.

Normalspannung bei Gesamtdehnung

In der Gleichung (2) wird deutlich, dass bei einer Gesamtdehnung auf eine Normalspannung gegeben ist. Grund dafür ist die auftretende mechanische Dehnung. Eine reine Wärmedehnung weist keine Normalspannung auf.

Wollen wir die Normalspannung berechnen, so können wir die obige Gleichung (2) nach dieser auflösen:

Merk’s dir!

Erinnerung: Bei einer reinen Wärmedehnung entstehen keine Spannungen!

Die Normalspannung die dabei entsteht, kann aus der Gleichung (2) berechnet werden:

$\epsilon_{ges} = \dfrac{\sigma}{E} + \alpha \cdot \triangle T$

$\epsilon_{ges} - \alpha \cdot \triangle T = \dfrac{\sigma}{E}$

$(\epsilon_{ges} - \alpha \cdot \triangle T) \cdot E = \sigma$

Es ergibt sich eine Normalspannung bei einer Gesamtdehnung zu:

$\sigma = (\epsilon_{ges} - \alpha \cdot \triangle T) \cdot E$ Normalspannung

In der obigen Gleichung ist deutlich zu erkennen, dass bei der Berechnung der Normalspannung die Wärmedehnung α ·ΔT von der Gesamtdehnung ε_ges abgezogen wird.

In dieser Lerneinheit wollen wir uns zwei Aufgaben zur Berechnung der Gesamtdehnung bzw. Längenänderung anschauen.

Aufgabe 1: Konstante Temperaturänderung

Aufgabenstellung

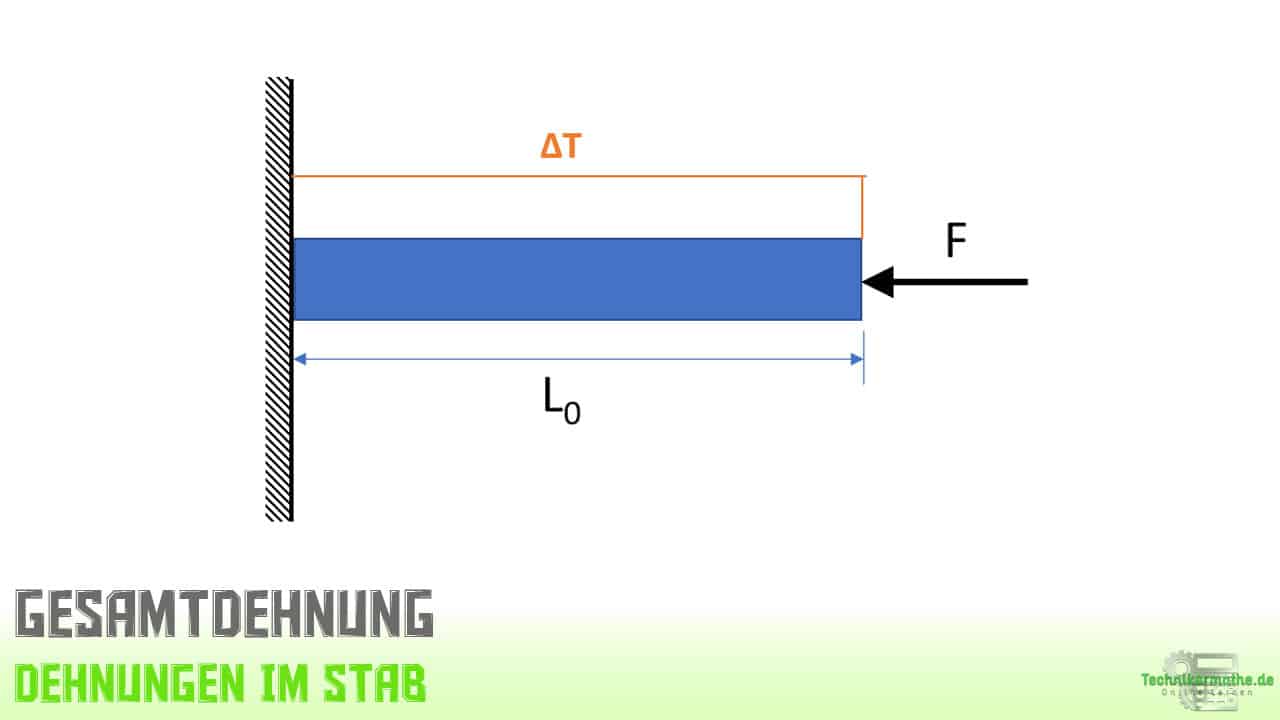
Gesamtdehnung, Dehnung im Stab, Wärmedehnung, Temperatur, konstante Temperatur, Druckkraft, Beispiel — Beispiel: Gesamtdehnung im Stab

Gegeben sei ein Stab, welcher am linken Ende fest eingespannt ist und am rechten Ende durch eine Druckkraft F belastet wird. Der Stab wird durch eine konstante Temperaturänderung ΔT im gesamten Stab belastet.

Wie groß muss die angreifende Kraft F sein, damit sich die Länge des Stabs nicht ändert?

Gegeben:

$L_0 = 1,5m$ , $A = 20mm^2$ , $\triangle T = 120 K$ , $E = 70.000 MPa$ , $\alpha = 23,1 \cdot 10^{-6} \frac{1}{K}$

Zunächst müssen wir die gegebenen Einheiten in SI-Einheiten umrechnen:

$A = 20mm^2 = 20 \cdot 10^{-6} m^2$

$E = 70.000 Mio. Pa$

Wir betrachten hier einmal eine Ausdehnung infolge der Temperaturdifferenz und zum anderen eine Dehnung infolge der Druckkraft F. Wir können hier also die Gleichung für die Gesamtdehnung heranziehen:

Gesamtdehnung

$\epsilon_{ges} = \dfrac{\sigma}{E} + \alpha \cdot \triangle T$

mit

$\sigma = \dfrac{N}{A} = \dfrac{-F}{A}$ Druckstab

Damit ergibt sich:

$\epsilon_{ges} = \dfrac{-F}{E \cdot A} + \alpha \cdot \triangle T$

In der Aufgabenstellung steht, dass sich der Stab nicht in seiner Länge ändern soll, damit tritt auch keine Dehnung auf:

$\epsilon_{ges} = 0$

Und damit:

$0 = \dfrac{-F}{E \cdot A} + \alpha \cdot \triangle T$

Auflösen nach der gesuchten Kraft F:

$\dfrac{F}{E \cdot A} = \alpha \cdot \triangle T$

$F = \alpha \cdot \triangle T \cdot E \cdot A$

Wir können nun alle Werte einsetzen und erhalten:

$F = 23,1 \cdot 10^{-6} \frac{1}{K} \cdot 120 K \cdot 70.000.000 Pa \cdot 20 \cdot 10^{-6} m^2 = 3880,8 N$

Bei einer Druckkraft von 3.880,8 N ist die Dehnung infolge der Temperaturänderung gleich der Stauchung infolge der Kraft F. Damit tritt keine Längenänderung auf!

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++