TM1 – Flächenschwerpunkt für zusammengesetzte Flächen

Der Flächenschwerpunkt ist der Schnittpunkt zweier Schwerelinien einer Fläche. Eine Schwerelinie ist eine Gerade, welche die gegebene Fläche so teilt, dass zwei gleich große Flächen entstehen.

In dieser Lerneinheit wollen uns anschauen, wie der Flächenschwerpunkt eines zusammengesetzten Körpers mittels Momentensatz bestimmt wird.

Für ein optimales Verständnis hilft dir ein anschauliches Rechenbeispiel zu dem Thema.

Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs TM1-Statik.

Flächenschwerpunkt, Momentensatz — Flächenschwerpunkt bestimmen

Flächenschwerpunkt: Gleichungen

Jeder Körper weist einen Schwerpunkt auf. Für bestimmte Flächen kennen wir die Schwerpunktlagen, wie zum Beispiel für Kreise, Dreiecke und Rechtecke. Haben wir also einen Körper gegeben, für welchen wir die Schwerpunktlage nicht kennen, dann können wir diesen ganz einfach in Flächen aufteilen, für welche wir die Schwerpunktlage kennen:

Flächenschwerpunkt, Nachhilfe Techniker, C-Profil, Teilflächen, Schwerpunkt — C-Profil in Teilflächen zerlegt

In der obigen Grafik ist ein C-Profil gegeben. Zur Bestimmung des Schwerpunktes kannst du das gegebene C-Profil Teilflächen aufteilen, für welche du die Schwerpunktlage kennst. Im obigen Beispiel haben wir das C-Profil also in drei rechteckige Fläche geteilt und die Schwerpunkte der drei Fläche genau mittig eingezeichnet.

Um den Gesamtschwerpunkt des C-Profils bestimmen zu können, wenden wir die folgenden Gleichungen an, die aus dem Momentensatz hergeleitet ist:

Schwerpunktlage in x-Richtung:

$x_S = \dfrac{x_1 \cdot A_1 + x_2 \cdot A_2 + ... + x_n \cdot A_n}{A_1 + A_2 + ... + A_n}$

$x_S = \dfrac{\sum x_i \cdot A_i}{\sum A_i}$

Schwerpunktlage in y-Richtung:

$y_S = \dfrac{y_1 \cdot A_1 + y_2 \cdot A_2 + ... + y_n \cdot A_n}{A_1 + A_2 + ... + A_n}$

$y_S = \dfrac{\sum y_i \cdot A_i}{\sum A_i}$

Um die obigen Gleichungen anwenden zu können, müssen wir vorab ein x,y-Koordinatensystem einführen. Die Abstände x_i und y_i sind dann die Abstände in x- und y-Richtung vom Koordinatenursprung hin zu den einzelnen Schwerpunkten der Teilflächen A_i.

Merk’s dir!

Hast du Aussparungen gegeben, so werden diese einfach als negative Flächen (-A_i) abgezogen.

Video: Flächenschwerpunkt für zusammengesetzte Flächen

Im folgenden Video zeigen wir dir, wie du den Flächenschwerpunkt für zusammengesetzte Flächen bestimmen kannst:

Prüfungsaufgabe 1: Flächenschwerpunkt bestimmen

Beispiel: Flächenschwerpunkt bestimmen, Nachhilfe Statik, Flächenschwerpunkt, Momentensatz, Beispiel — Beispiel: Flächenschwerpunkt bestimmen

Aufgabenstellung

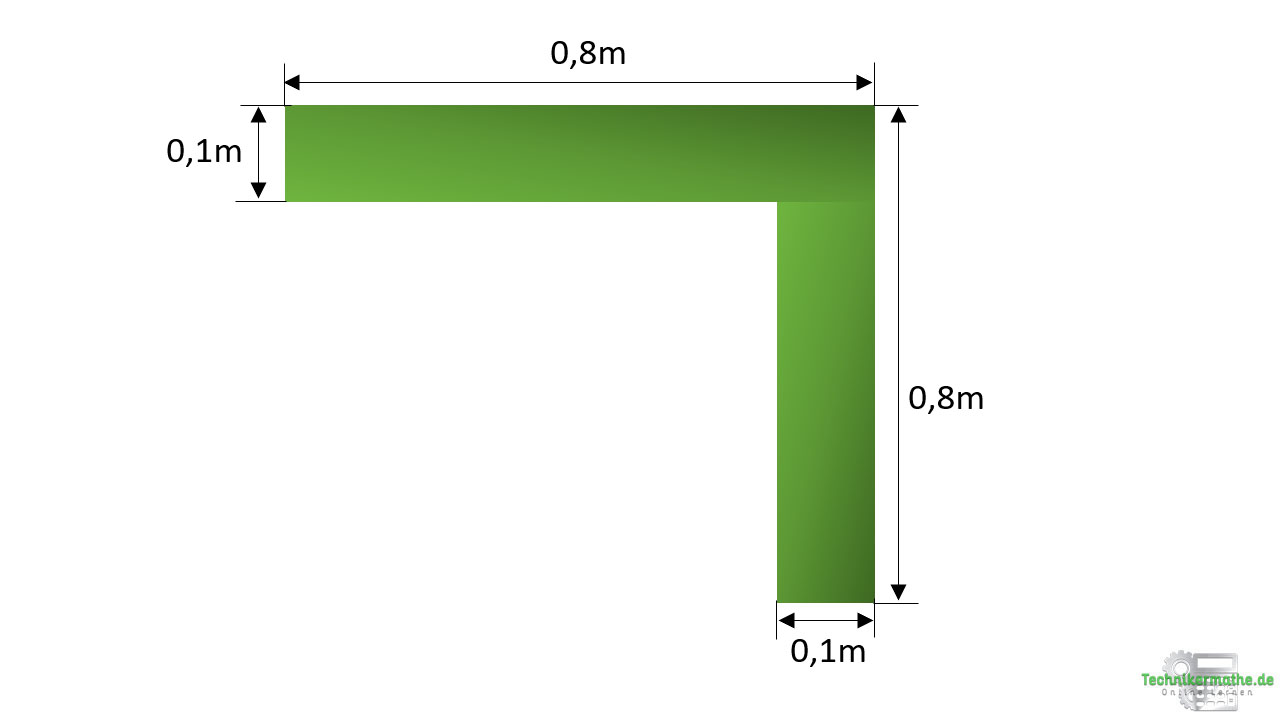
Gegeben sei das obige Profil mit den gegebenen Abmessungen.

Bestimme den Flächenschwerpunkt des gegebenen Profils!

Wir wollen den Gesamtschwerpunkt des obigen Profils bestimmen. Dazu können wir das Profil zunächst in Teilflächen zerlegen und die Schwerpunkte der Teilflächen einzeichnen:

Flächenschwerpunkt, Prüfungsvorbereitung Techniker, Momentensatz, Schwerpunkt, C-Profil — Teilflächen und Schwerpunktlage

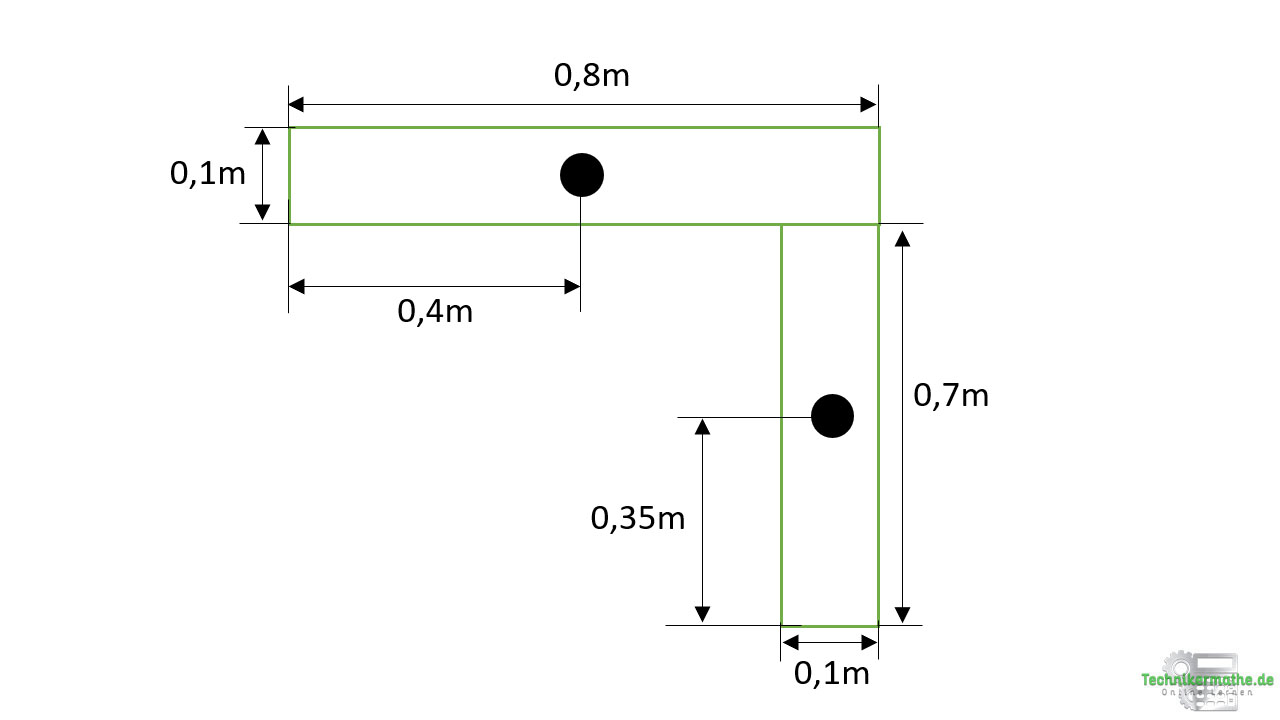
Da es sich um zwei rechteckige Flächen handelt, liegt der Schwerpunkt genau in der Mitte. Die Abmessungen haben wir entsprechend angepasst. Als nächstes führen wir ein x,y-Koordinatensystem ein. Dieses sollte – wenn nicht bereits in der Aufgabe gegeben – so eingeführt werden, dass die Abmessungen vom Koordinatensystem hin zu den Schwepunkten gegeben sind. Dazu legst du das Koordinatensystem am Besten an eine Ecke des Profils:

Flächenschwerpunkt bestimmen, Koordinatensystem, Flächenschwerpunkt, C-Profil, Momentensatz — Flächenschwerpunkt bestimmen – Koordinatensystem einführen

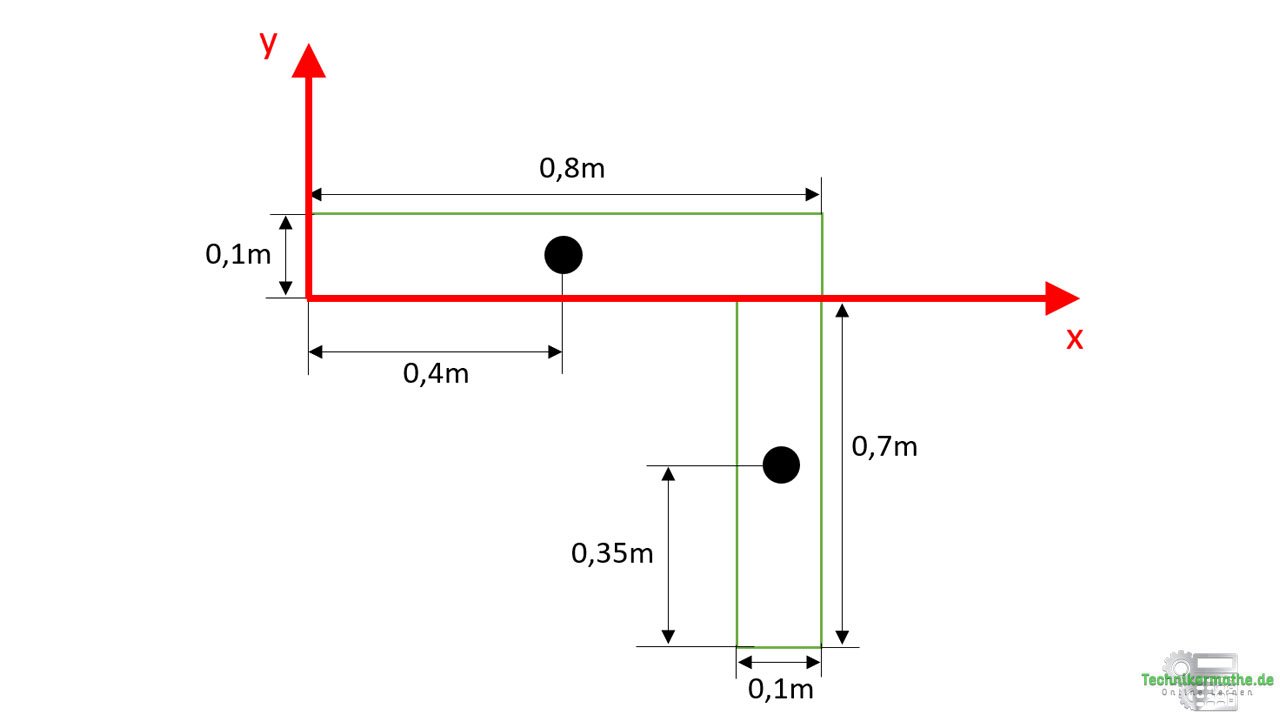
Im nächsten Schritt wenden wir die beiden Formeln zur Bestimmung des Gesamtschwerpunktes an. Wir starten mit der Berechnung des Gesamtschwerpunktes in x-Richtung. Dazu müssen wir nun die Abstände in x-Richtung vom Koordinatensystem hin zu den einzelnen Schwerpunkten betrachten (y-Achse wurde dazu verlängert):

Flächenschwerpunkte bestimmen, Schwerpunkt berechnen, Flächenschwerpunkt, Momentensatz — Flächenschwerpunkt bestimmen – Abstände in x-Richtung

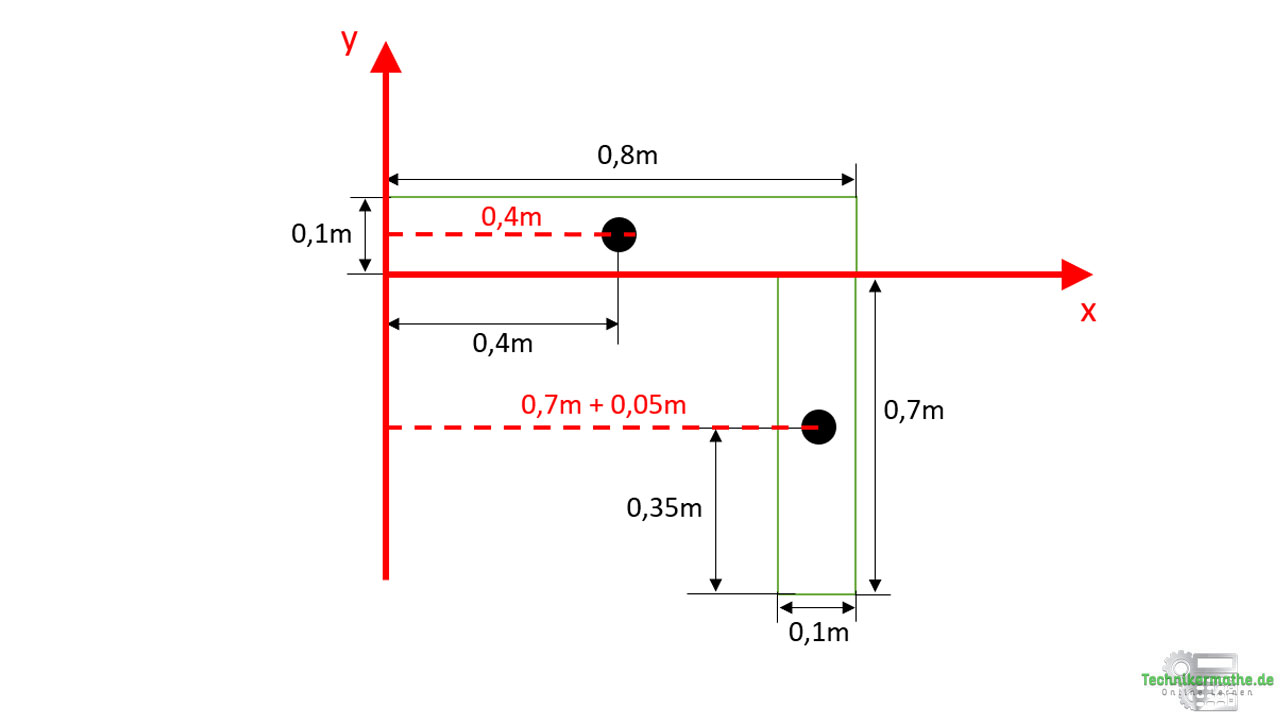
Da wir uns von der y-Achse in positive x-Richtung bis hin zu den Schwerpunkten bewegen, sind die Abstände positiv. Zum ersten Schwerpunkt ist ein Abstand von 0,4m gegeben, zum zweiten Schwerpunkt ein Abstand von 0,75m in x-Richtung. Die Flächen A₁ = 0,1m · 0,8m und A₂ = 0,1m · 0,7m der beiden Teilflächen müssen wir innerhalb der Formel ebenfalls berücksichtigen:

$x_S = \dfrac{\sum x_i \cdot A_i}{\sum A_i} = \dfrac{x_1 \cdot A_1 + x_1 \cdot A_2}{A_1 + A_2}$

$x_S = \dfrac{0,4m \cdot (0,1m \cdot 0,8m) + 0,75m \cdot (0,1m \cdot 0,7m)}{(0,1m \cdot 0,8m) + (0,1m \cdot 0,7m)}$

$x_S = 0,56 m$

Der Abstand vom Koordinatenursprung zum Gesamtschwerpunkt in x-Richtung beträgt 0,56 m.

Wir benötigen als nächstes den Abstand in y-Richtung:

Flächenschwerpunkt bestimmen, Flächenschwerpunkt, C-Profil — Flächenschwerpunkt bestimmen – Abstände in y-Richtung

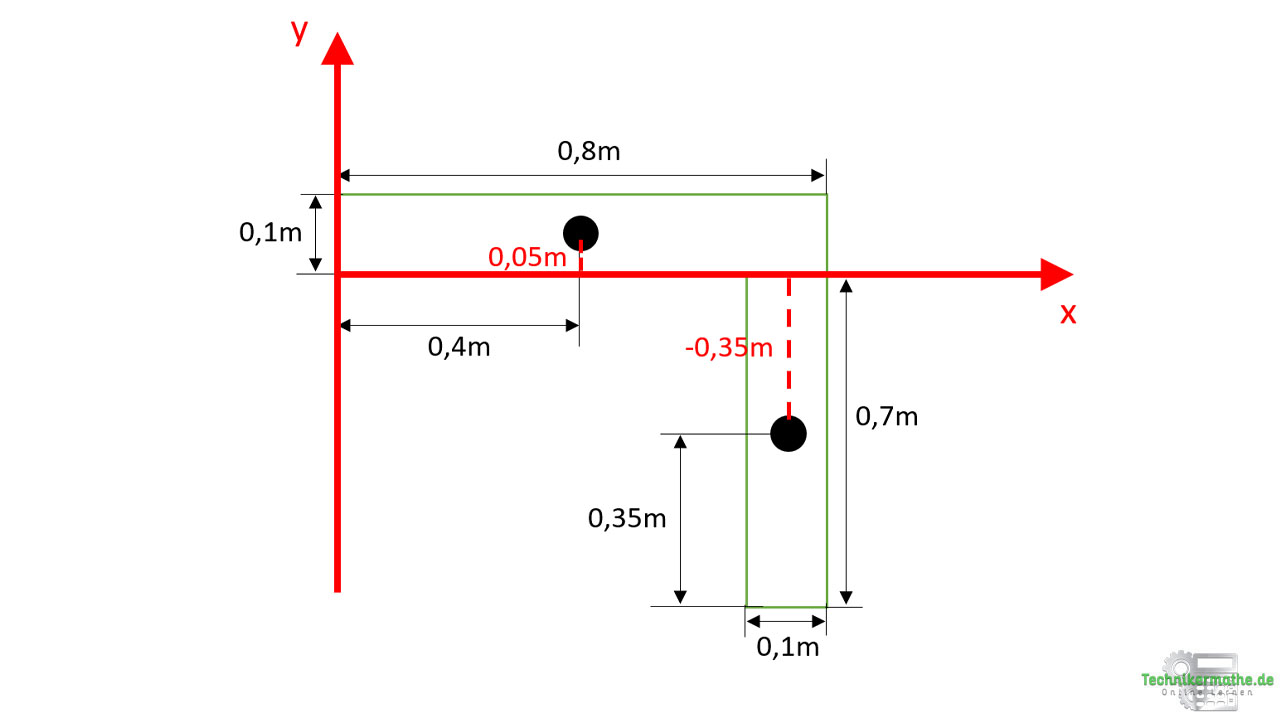
Der Abstand von 0,05m von der x-Achse zum ersten Schwerpunkt erfolgt in positive y-Richtung, der Abstand von -0,35m von der x-Achse zum zweiten Schwerpunkt in negative y-Richtung. Dieser Abstand wird also negativ berücksichtigt. Die Flächen A₁ = 0,1m · 0,8m und A₂ = 0,1m · 0,7m der beiden Teilflächen müssen wir innerhalb der Formel ebenfalls berücksichtigen:

$y_S = \dfrac{\sum y_i \cdot A_i}{\sum A_i} = \dfrac{y_1 \cdot A_1 + y_1 \cdot A_2}{A_1 + A_2}$

$y_S = \dfrac{0,05m \cdot (0,1m \cdot 0,8m) - 0,35m \cdot (0,1m \cdot 0,7m)}{(0,1m \cdot 0,8m) + (0,1m \cdot 0,7m)}$

$y_S = -0,14 m$

Der Abstand vom Koordinatenursprung zum Gesamtschwerpunkt in y-Richtung beträgt -0,14 m.

In der nachfolgenden Grafik ist der Schwerpunkt des Gesamtprofils eingezeichnet. Dieser befindet sich außerhalb des Körpers:

Flächenschwerpunkt bestimmen, Flächenschwerpunkt, Gesamtschwerpunkt, C-Profil — Flächenschwerpunkt

Was kommt als Nächstes?

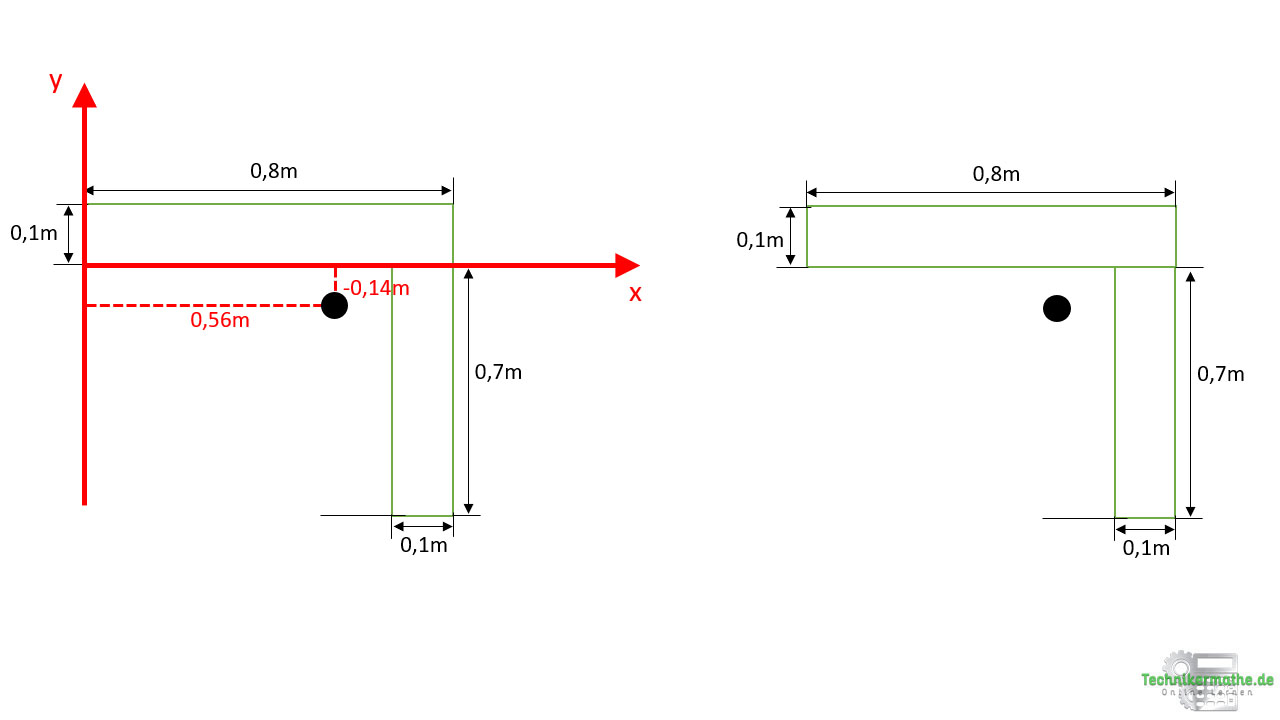
In der folgenden Lerneinheit betrachten wir ein weitere Aufgabe mit Aussparung zur Bestimmung des Gesamtschwerpunktes einer Fläche, indem wir diese in Teilflächen teilen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++