(ET5-10) Reihenschaltung von Widerstand und Kondensator [RC-Element]

In diesem Kurstext betrachten eine Wechselstromschaltung. Genauer gesagt die Reihenschaltung von R und C, also von Widerstand und Kondensator (Kapazität).

Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET6-Wechselstromtechnik 1

Die Vertiefung der Wechselstromtechnik findest du im Kurs: ET7-Wechselstromtechnik 2

Reihenschaltung von R und C – Vorgehensweise – Überblick

Damit du nicht immer zwischen den Texten blättern musst. Findest du nachfolgend noch mal den Überblick für die einzelnen Teilschritte.

Die Vorgehensweise erfolgt immer nach einem gleichbleibenden Schema:

I. Zuerst entwerfen wir den zugehörigen Schaltplan und versehen ihn mit die passenden sowie notwendigen Zählpfeilen und Zeigerangaben.

II. Danach formulieren wir mit dem Maschensatz und dem Knotensatz die passenden Kirchhoff’schen Gesetze

III. Im Anschluss daran folgt die Anfertigung des Zeigerbildes basierend auf unseren Angaben

IV. Anschließend folgt die Berechnung der Beträge der Größen Spannung und Strom

V. Abschließend bestimmen wir den Phasenverschiebungswinkel.

Reihenschaltung von R und C – Schaltplan mit Zählpfeilen anfertigen

Nachfolgend findest du den Schaltplan mit einer Reihenschaltung von Widerstand und Kapazität (Kondensator) mit der Angabe der zugehörigen Spannungen, der Quellenspannung sowie dem elektrischen Strom.

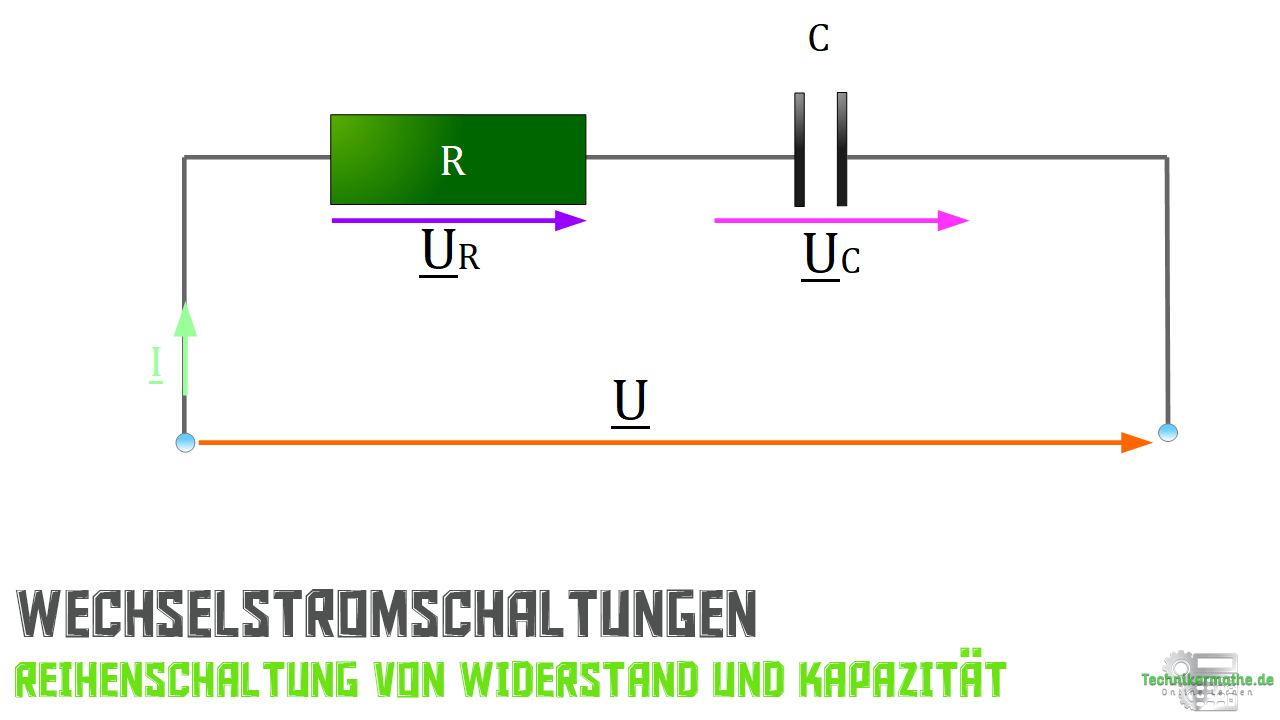
Wie du weißt, besitzt die Wechselspannung den Effektivwert $U$ und die Kreisfrequenz $\omega = 2 \pi \cdot f$

Wie im vorherigen Beispiel suchen wir den Wert für die Netzspannung, den Phasenverschiebungswinkel zwischen Netzspannung und Netzstrom, sowie den Wert für die aufgenommene Leistung und die verrichtete Arbeit.

Reihenschaltung von R und C – Maschensatz aufstellen

Wie du weißt, besagt der Maschensatz, dass die Summe aller Spannung gleich null ist.

$\sum \underline{U} = 0$

Für einen kompletten Umlauf in unserem Schaltplan erhalten wir die folgende Gleichung:

$\underline{U}_R + \underline{U}_C = \underline{U}$

An die Gleichung des Maschensatzes angepasst erhalten wir dann:

$\sum \underline{U} = \underline{U}_R + \underline{U}_C - \underline{U} = 0$

Reihenschaltung von R und C – Zeigerbild anfertigen

Mit Hilfe der obigen Gleichung können wir nun ein Zeigerbild erzeugen. Jede Spannung wird als Spannungszeiger erfasst. Die gemeinsame Wechselgröße ist hier der elektrische Strom, da dieser sowohl für den Widerstand $R$ als auch für die Kapazität $C$ gleich ist.

Im ersten Schritt zeichnen wir den Stromzeiger $\underline{I}$ des elektrischen Stroms als horizontalen Pfeil:

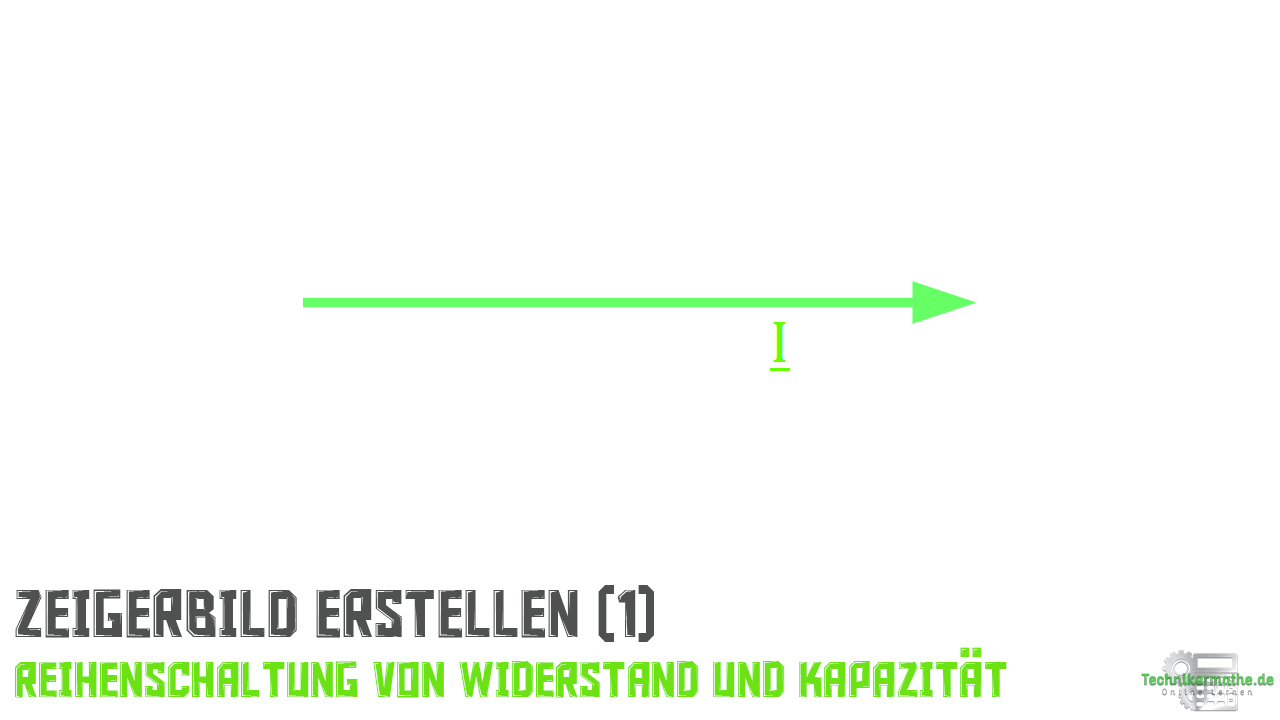
Reihenschaltung von R und C - Stromzeiger — Reihenschaltung von R und C – Stromzeiger

Im zweiten Schritt zeichnen wir den Spannungszeiger des Widerstandes $\underline{R}_R$ ein, welcher in der gleichen Phase liegt wie der Stromzeiger $\underline{I}$ .

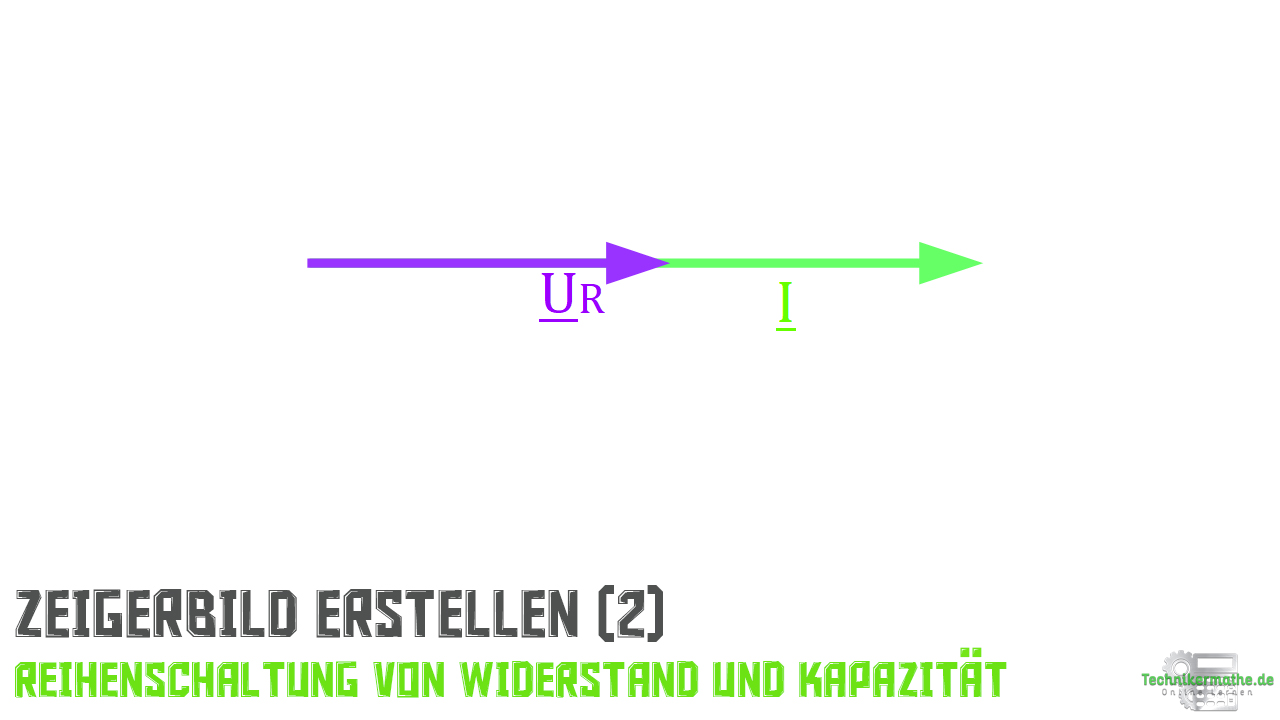
Reihenschaltung von R und C - Spannungszeiger (Widerstand) — Reihenschaltung von R und C – Spannungszeiger (Widerstand)

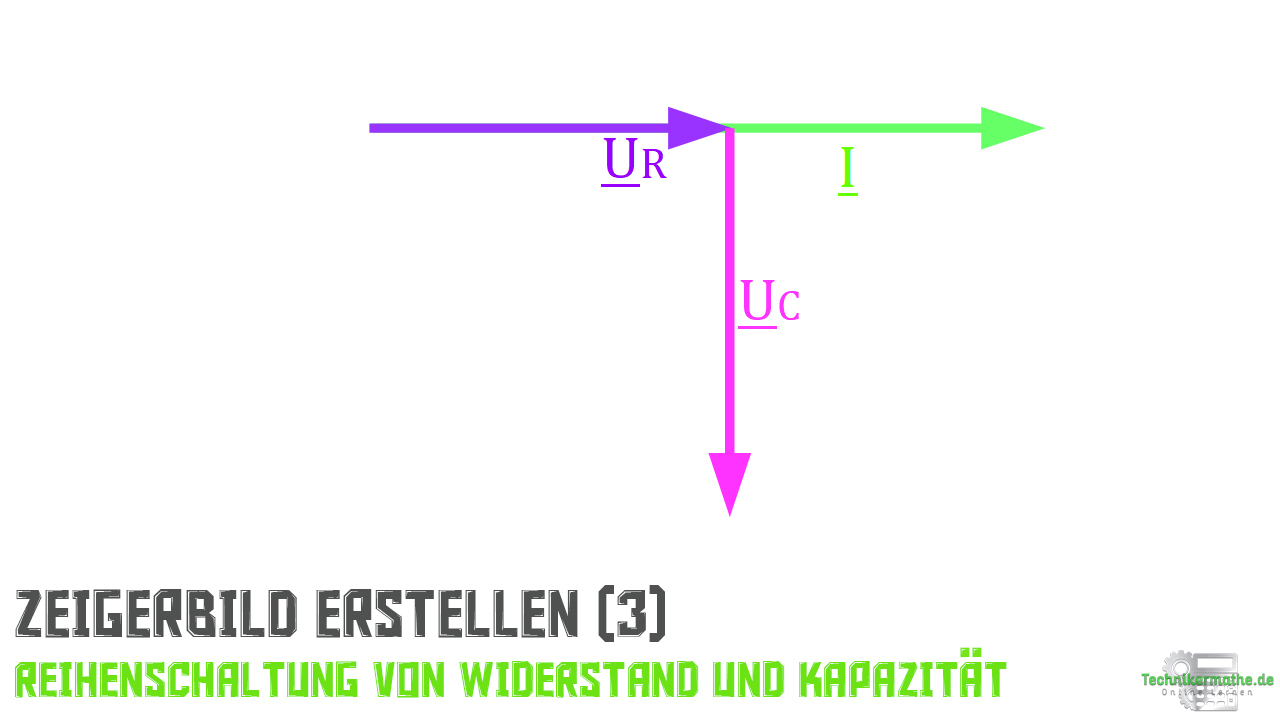
Im dritten Schritt zeichnen wir den Spannungszeiger der Kapazität $\underline{U}_C$ ein, dessen Ende wird an die Spitze des Spannungszeigers des Widerstandes $\underline{U}_R$ angezeichnet. Dabei ist zu beachten, dass dieser dem Stromzeiger um $90°$ nacheilt, weshalb der vertikal nach unten eingezeichnet wird.

Reihenschaltung von R und C - Spannungszeiger (Kapazität) — Reihenschaltung von R und C – Spannungszeiger (Kapazität)

Im vierten Schritt zeichnen wir vom Ursprung ausgehend den Spannungszeiger $\underline{U}$ ein, welche aufgrund der geometrischen Vektoraddition mit seiner Spitze an der Spitze des Spannungszeigers der Induktivität $\underline_{U}_C$ endet.

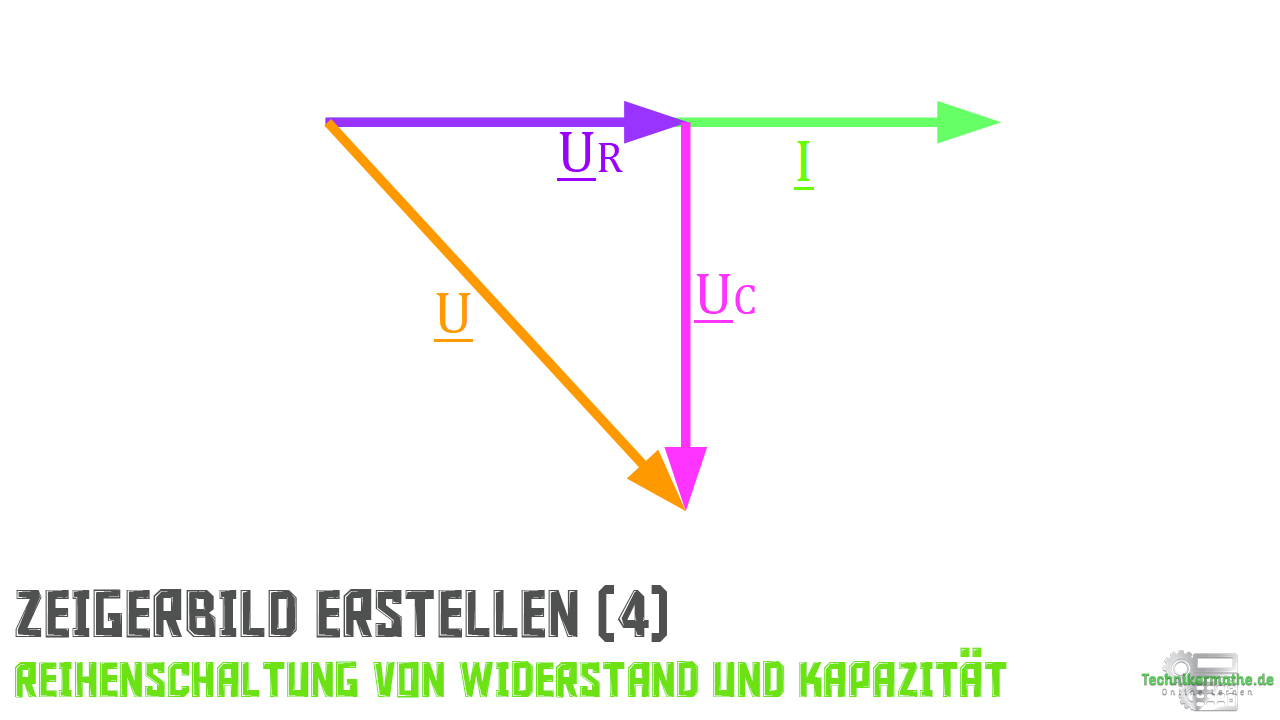
Reihenschaltung von R und C - Spannungszeiger (Netzspannung) — Reihenschaltung von R und C – Spannungszeiger (Netzspannung)

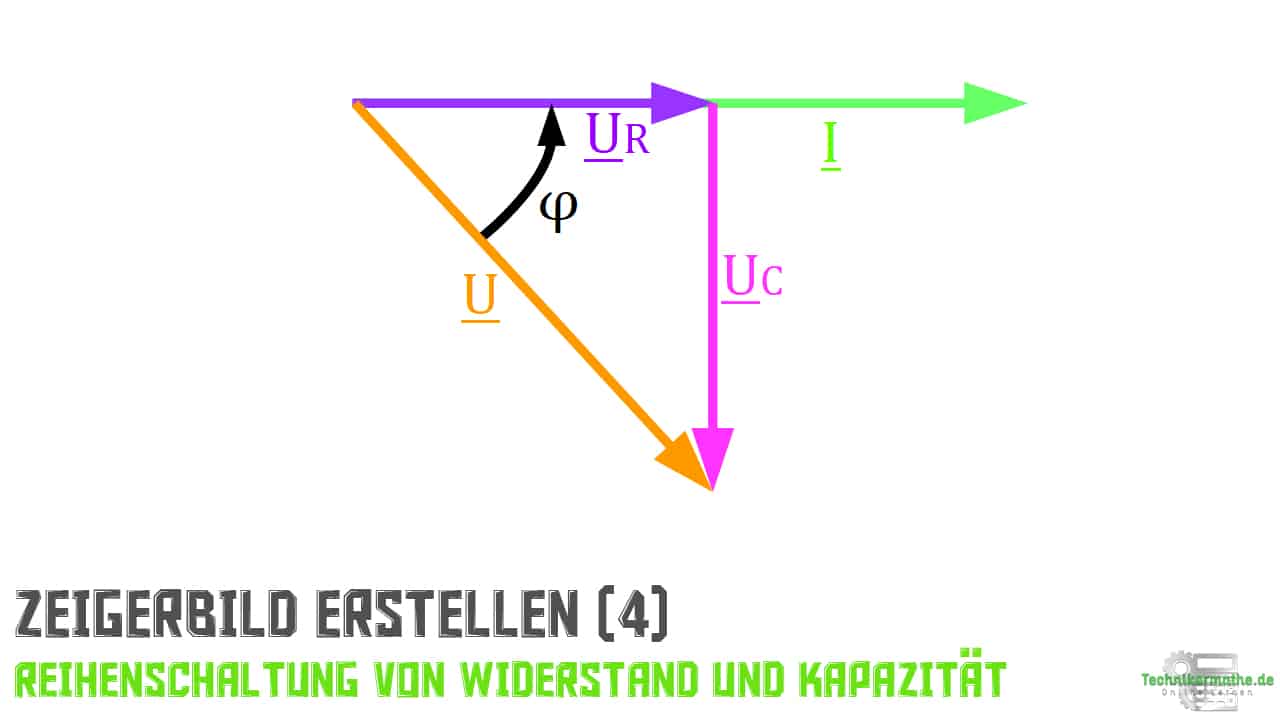
Unser Zeigerbild ist nun fast vollständig. Wir greifen jetzt aber kurz vor und zeichnen schon ein mal den Phasenverschiebungswinkel $\varphi$ ein.

Reihenschaltung von R und C - Phasenverschiebungswinkel — Reihenschaltung von R und C – Phasenverschiebungswinkel

Reihenschaltung von R und C – Netzspannung und Scheinwiderstand berechnen

Jetzt können wir unter Verwendung des Ohm’schen Gesetzes und in Hinblick auf das rechtwinklige Spannungsdreieck die Spannungen für den Widerstand und die Induktivität ermitteln:

Berechnung der Spannungen bei R und C

$U_R = I \cdot R$ | Spannung am Widerstand

Kennzahlen:

$U_R =$ Spannung am Widerstand

$I =$ Vorliegender Strom

$R =$ Widerstandswert

sowie

$U_C = \frac{I}{\omega \cdot C }$ | Spannung an der Kapazität

Kennzahlen:

$U_C =$ Spannung an der Kapazität

$I =$ Vorliegender Strom

$R =$ Widerstandswert

$\omega =$ Kreisfrequenz

Berechnung der Netzspannung

Da es sich um ein rechtwinkliges Spannungsdreieck handelt wenden wir den Satz des Pythagoras an um die Netzspannung zu errechnen:

$U = \sqrt{ U_R^2 + U_C^2}$

Unter Einsatz der obigen beiden Gleichungen erhalten wir:

$U = \sqrt{ U_R^2 + U_C^2}$ | Netzspannung

$U = I \sqrt{ R^2 + (\frac{1}{\omega \cdot C})^2}$ | Netzspannung

Berechnung des Scheinwiderstandes

Zusätzlich können wir auch noch den Scheinwiderstand errechnen.

Der Scheinwiderstand $Z$ errechnet sich aus dem Quotienten von Spannung und Stromstärke.

$Z = \frac{U}{I}$ | Scheinwiderstand

Unter Verwendung der Gleichung für die Netzspannung erhalten wir angepasst für den Scheinwiderstand:

$Z = \sqrt{ R^2 + (\frac{1}{\omega \cdot C})^2}$ | Scheinwiderstand

Reihenschaltung von R und C – Phasenverschiebungswinkel berechnen

Der Phasenverschiebungswinkel kann ebenfalls unter Hinzunahme des Zeigerbildes berechnet werden. Die zugehörige Formeln hierzu ist:

$tan \varphi = - \frac{U_L}{U_C}$

Unter Verwendung der obigen Gleichungen für die Spannungen an Widerstand und Induktivität erhalten wir, als angepasste Gleichung:

$tan \varphi = - \frac{1}{R \cdot \omega \cdot L}$ | Phasenverschiebungswinkel

Reihenschaltung von R und C – Leistung und Arbeit berechnen

Falls es von dir erwünscht oder in der Aufgabenstellung gefordert wird, kannst du noch die Leistung und die Arbeit dieser Schaltung berechnen.

Berechnung der Leistung

Zur Berechnung der Leistungen, welche vom der Schaltung aufgenommen wird, passen wir die allgemeinen Gleichungen einfach an:

Leistung

Aus $P = U \cdot I$ wird $\rightarrow$

$P = U \cdot I cos \varphi$

Blindleistung

Aus $Q = U \cdot I$ wird $\rightarrow$

$Q = U \cdot I sin \varphi$

Scheinleistung

Die Scheinleistung errechnet sich wie gewohnt.

$S = U \cdot I$

Berechnung der Arbeit

Die Berechnung der Arbeit, die verrichtet wird im einen Zeitraum t, erfolgt ja aus dem Produkt von Leistung $P$ oder $Q$ und dem Faktor Zeit $t$

Arbeit

Aus $W = P \cdot t$ wird $\rightarrow$

$W = U \cdot I cos \varphi \cdot t$

Blindarbeit

Aus $W= Q \cdot t$ wird $\rightarrow$

$W = U \cdot I sin \varphi \cdot t$

Was kommt als Nächstes?

Nachdem du jetzt weißt wie mit einer Reihenschaltung von Widerstand und Kapazität umzugehen ist und welche Größen hierbei berechnet werden können, behandeln wir im kommenden Kurstext die Parallelschaltung eines Widerstandes und einer Induktivität.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++