In diesem Kurstext vermitteln wir dir ein Grundverständnis für das Zeigerdiagramm, Zeiger und Zeigerbilder bei Wechselspannung und Wechselstrom. Auch das t-I-Diagramm und das t-U-Diagramm lernst du im Zusammenhang mit Stromzeigern und Spannungszeigern kennen.
Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema. Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET6-Wechselstromtechnik 1 Die Vertiefung der Wechselstromtechnik findest du im Kurs: ET7-Wechselstromtechnik 2
Das T-U-Diagramm, auch als “Phasendiagramm” bekannt, ist ein grafisches Werkzeug, das in der Wechselstromtechnik verwendet wird, um die Beziehung zwischen Spannung (U) und Zeit (T) darzustellen. Es wird oft verwendet, um die Phasenverschiebung zwischen Spannung und Strom in einem Wechselstromkreis zu visualisieren.
In einem T-U-Diagramm werden die Zeit auf der horizontalen Achse (T-Achse) und die Spannung auf der vertikalen Achse (U-Achse) dargestellt. Durch die grafische Darstellung des zeitlichen Verlaufs der Spannung können Phasenverschiebungen zwischen Spannung und Strom leicht erkannt werden.
Dieses Diagramm ist besonders nützlich, um Phasenverschiebungen in induktiven und kapazitiven Schaltkreisen zu analysieren. Zum Beispiel wird in einem rein induktiven Schaltkreis die Stromwelle im Vergleich zur Spannungswelle um 90 Grad verzögert, während sie in einem rein kapazitiven Schaltkreis um 90 Grad vorausgeht.
Das T-U-Diagramm ist ein wertvolles Instrument für Ingenieure und Techniker, um das Verhalten von Wechselstromschaltkreisen zu verstehen und zu analysieren.
Zeigerdiagramm – Grundlagen
Du kennst ja bereits das Prinzip aus der Gleichstromtechnik aber das Vollständigkeit halber hier noch mal angepasst für die Wechselstromtechnik:
Liegt an einem Ohmschen Leiter eine sinusförmige Wechselspannung an, so fließt durch den Widerstand ein elektrischer Strom, dessen Intensität von der Höhe der angelegten Spannung und dem Widerstandswert des Widerstandes abhängig ist.
Sowohl der elektrische Strom, als auch die elektrische Spannung erreichen ihren Nulldurchgang, ihren maximalen Scheitelwert und ihren minimalen Scheitelwert gleichzeitig.
Da es sich um einen Ohmschen Leiter handelt, ist die Phasenverschiebung zwischen Strom und Spannung gleich Null.
Um sich ein anschaulichen Überblick zum zeitlichen Verlauf von Spannung und Strom zu verschaffen, empfiehlt es sich die einzelnen Werte im Zeitverlauf in ein t-U-Diagramm sowie ein t-I-Diagramm zu überführen.
Die Wechselstromtechnik nutzt darüber hinaus die Zeigerdiagramme, welche besonders leicht zu erstellen sind.
Es kann ein zeichnerischer Zusammenhang zwischen dem Zeigerdiagramm und dem jeweiligen t-U-Diagramm sowie t-I-Diagramm hergestellt werden.
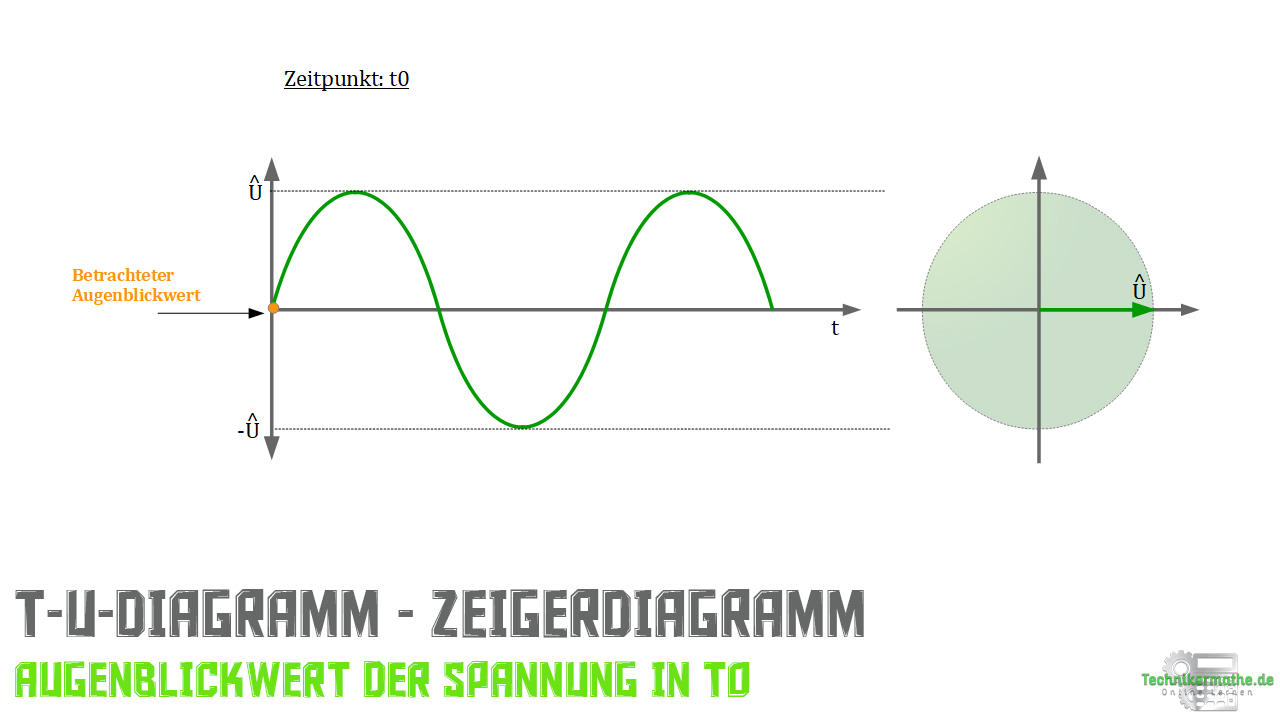
Um einen Wert im t-U-Diagramm oder t-I-Diagramm auf ein Zeigerdiagramm zu übertragen, legt man das Zeigerdiagramm mit den gleichen Maßen zum Kurvenverlauf des t-U- oder t-I-Diagramm zeichnerisch direkt neben die Diagramme.
Wenn man nun die Kurve abfährt, kann man für jeden Zeitpunkt durch eine horizontale Verschiebung des zugehörigen Punktes auf der Kurve bis hin zum Zeigerdiagramm eine passende Spannung ![]() abbilden, wobei dessen Zeigerspitze immer deckungsgleich mit dem verschobenen Punkt ist.
abbilden, wobei dessen Zeigerspitze immer deckungsgleich mit dem verschobenen Punkt ist.
Wenn dir das eventuell noch zu kompliziert ist, dann schaue dir einfach die nachfolgenden 6 Bilder an. Hier sind unterschiedliche Punkte verschoben worden.
Zeigerdiagramm – t-U-Diagramm
Um die Sinusförmige Wechselspannung für einen beliebigen Wert im t-U-Diagramm darstellen zu können, lässt man den Zeiger mit der Länge der Spannungsamplitude ![]() mit einer zugehörigen Winkelgeschwindigkeit
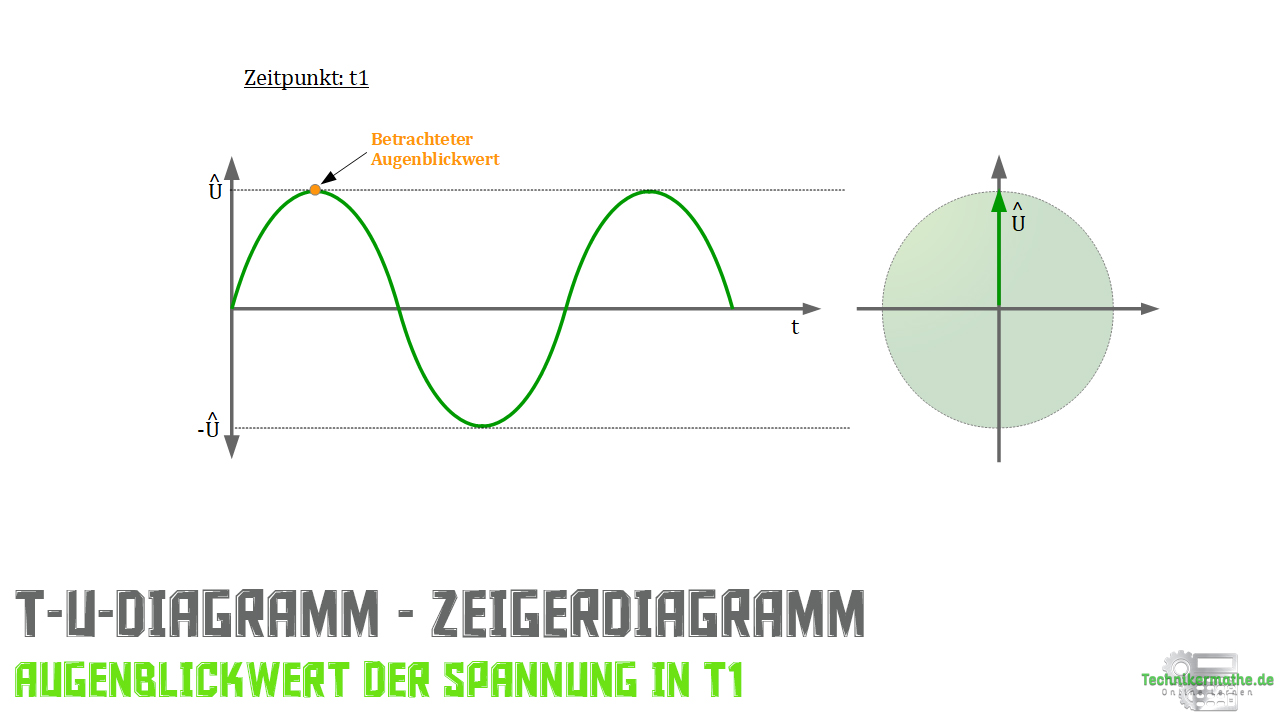
mit einer zugehörigen Winkelgeschwindigkeit ![]() gegen den Uhrzeigersinn rotieren. Auf der Ordinate lässt sich dann immer der jeweilige Augenblickwert der Wechselspannung ablesen.
gegen den Uhrzeigersinn rotieren. Auf der Ordinate lässt sich dann immer der jeweilige Augenblickwert der Wechselspannung ablesen.
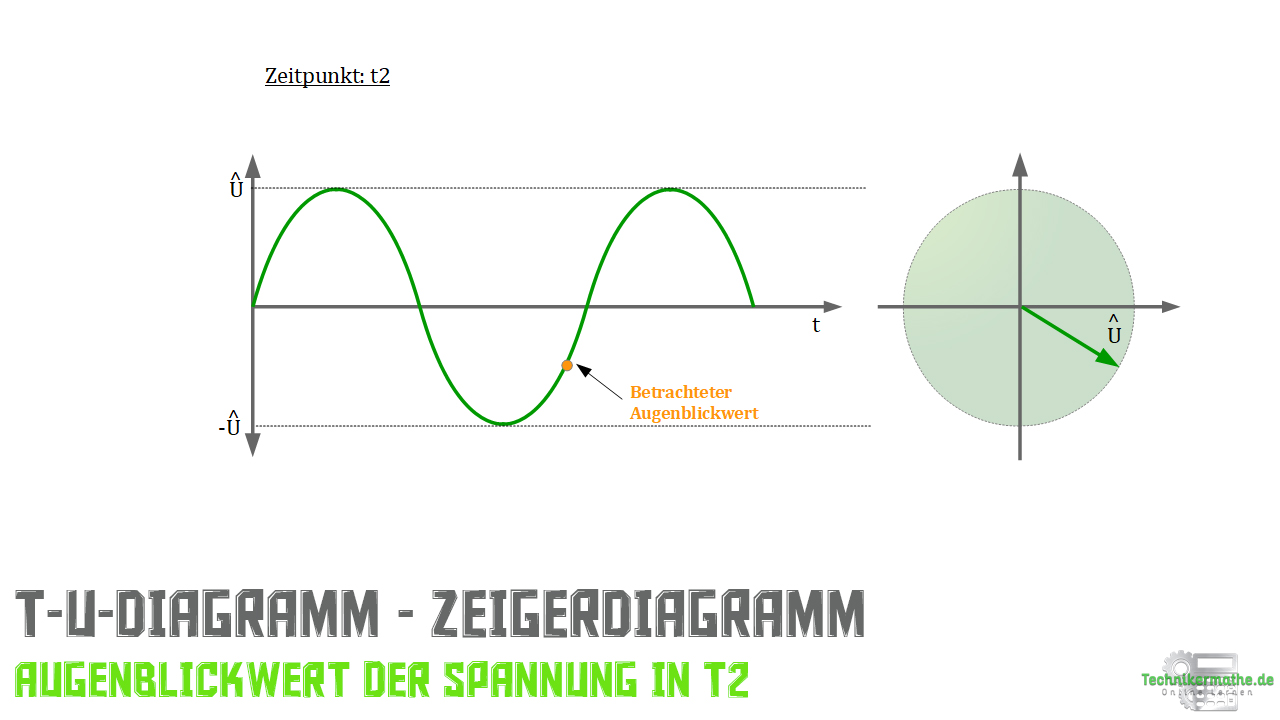
Dieser Vorgang ist für drei Punkte auf der Kurve im t-U-Diagramm dargestellt.

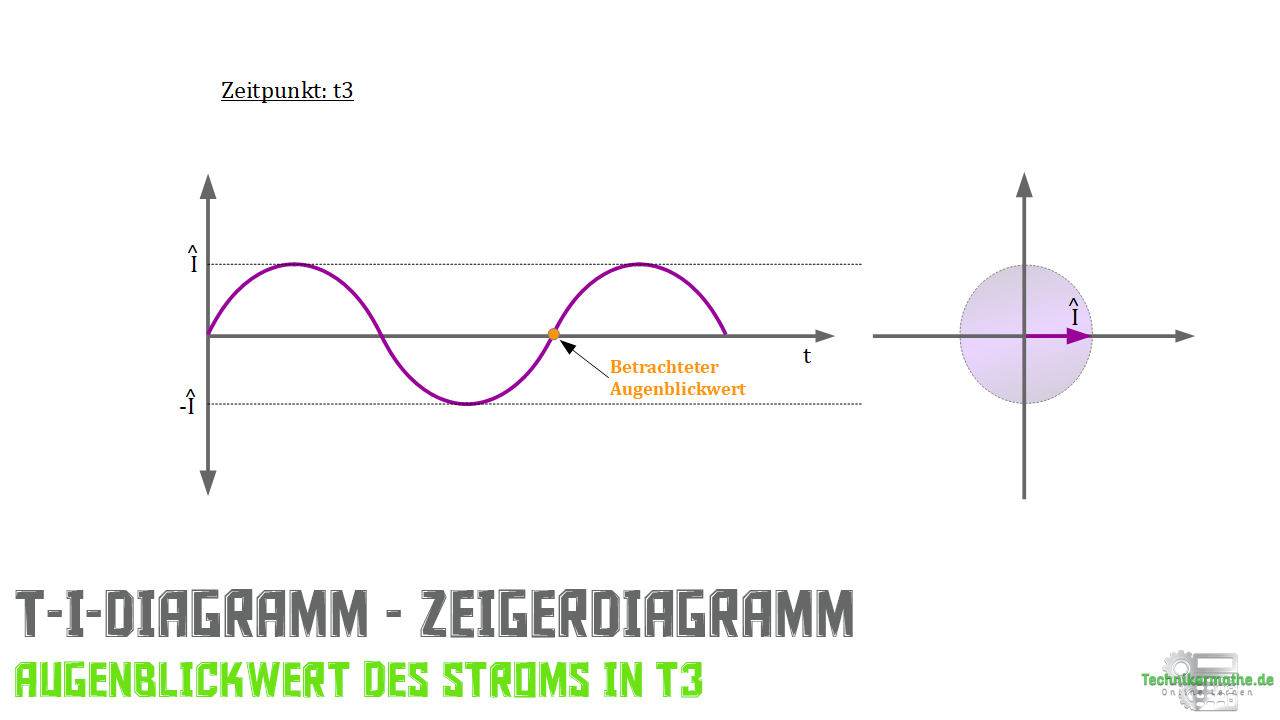
Zeigerdiagramm – t-I-Diagramm
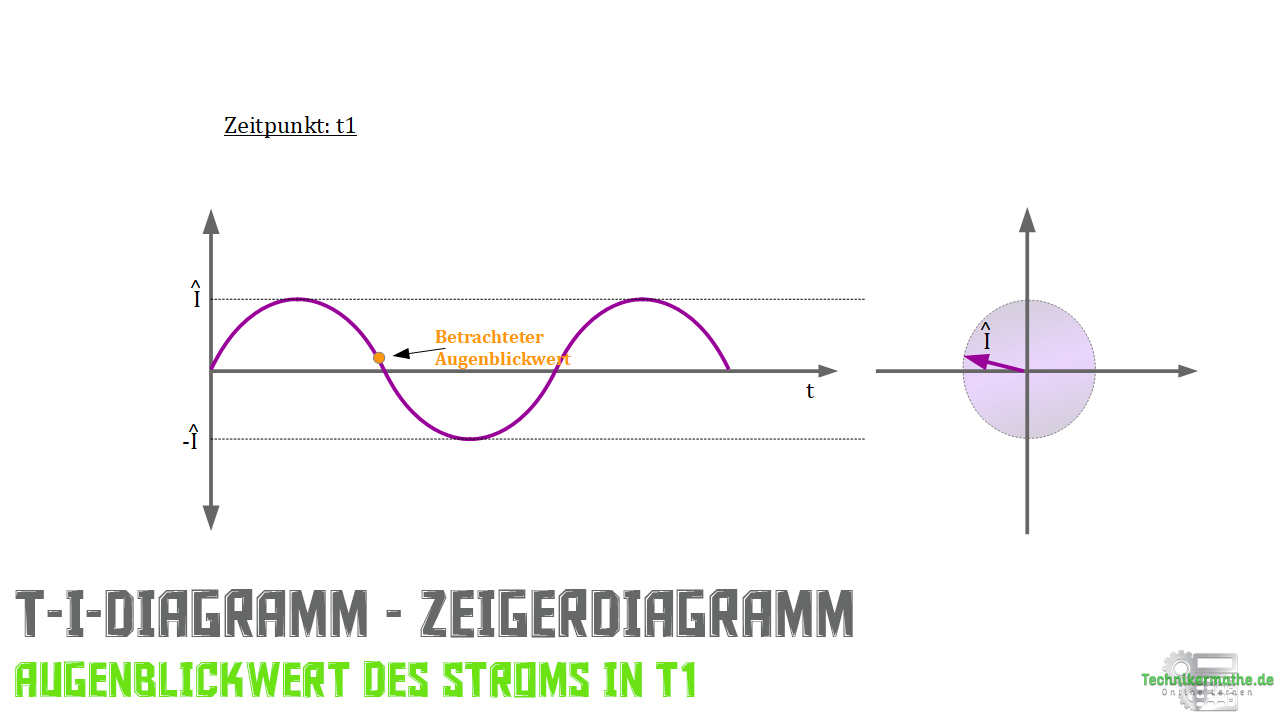
Auch der sinusförmige Wechselstrom kann für einen beliebigen Wert im t-I-Diagramm dargestellt werden. Wieder lässt man den Zeiger jetzt mit der Länge der Wechselstromamplitude ![]() und der zugehörigen Winkelgeschwindigkeit
und der zugehörigen Winkelgeschwindigkeit ![]() gegen den Uhrzeigersinn rotieren. Auf der Ordinate lässt sich dann immer der jeweilige Augenblickwert des Wechselstroms ablesen.
gegen den Uhrzeigersinn rotieren. Auf der Ordinate lässt sich dann immer der jeweilige Augenblickwert des Wechselstroms ablesen.
Wieder stellen wir den Vorgang für drei Punkte auf der Kurve im t-I-Diagramm dar.

Zeigerdiagramm – t-U-Diagramm – Summenspannung bilden
Ein besonderer Vorteil von Zeigerdiagrammen besteht darin, dass es uns erlaubt phasenverschobene, gleichfrequente Spannungen mit unterschiedlichen Amplituden zu addieren.
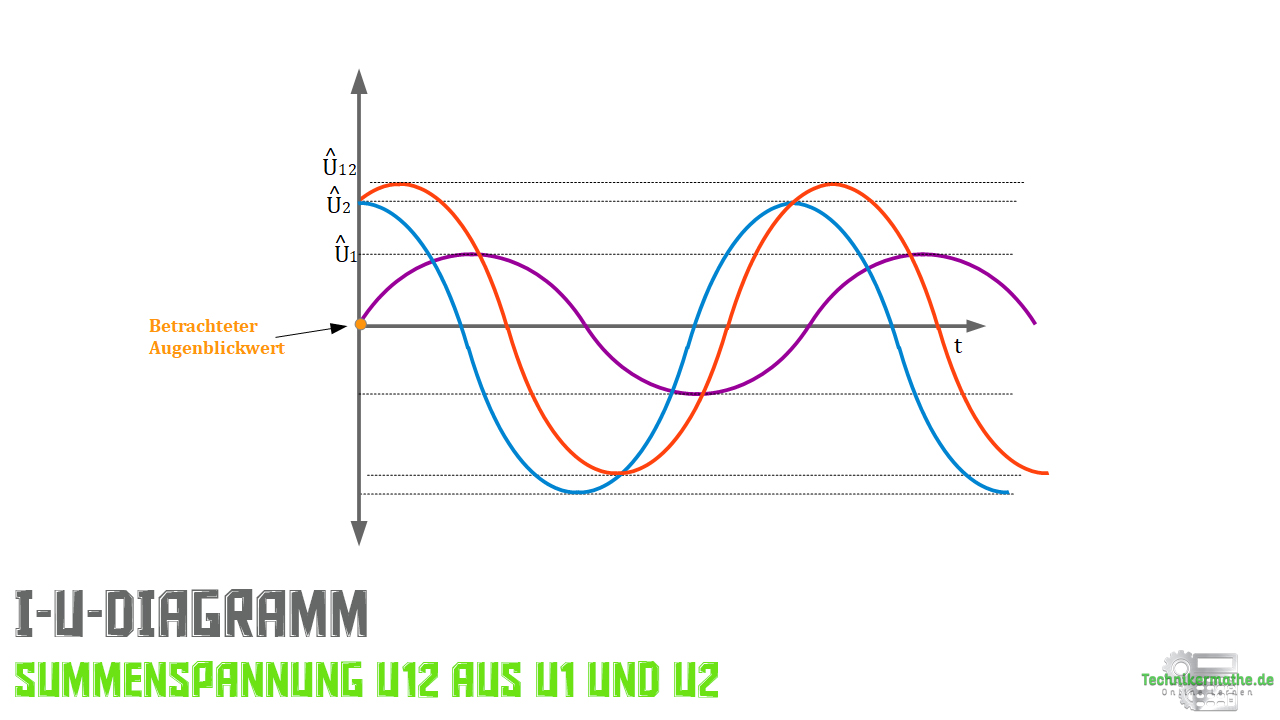
Summenspannung im t-U-Diagramm
In dem t-U-Diagramm siehst du zwei Spannungen ![]() und
und ![]() . Beide Sinuskurven bilden zusammen durch einfach Addition eine dritte Sinuskurve, die Summenspannung
. Beide Sinuskurven bilden zusammen durch einfach Addition eine dritte Sinuskurve, die Summenspannung ![]() . Diese Darstellung soll auch stellvertretend für den Summenstrom im t-I-Diagramm erfolgen
. Diese Darstellung soll auch stellvertretend für den Summenstrom im t-I-Diagramm erfolgen
Summenspannung im Zeigerdiagramm
Mit Hilfe des Zeigerdiagramms lässt sich die Summenspannung wesentlich schneller durchführen als mit der Addition der Sinuskurven. Denn alle drei Spannungen weisen die gleiche Frequenz auf, womit ihre Zeiger mit der gleichen Winkelgeschwindigkeit rotieren.
Zeigerdiagramm – Zusammensetzung der Zeiger
Ähnlich wie in der Mechanik, wo Kräfte addiert werden, bildet sich der Summenzeiger durch eine vektorielle Addition aus den Zeigern der Teilspannungen.
Im vorherigen Kurstext haben wir den Knotensatz und den Maschensatz für Wechselströme und Wechselspannungen behandelt. Dieses Wissen greifen wir nun auf.
- In der Wechselstromtechnik besagt der Knotensatz, dass die Augenblickwerte der Wechselströme zusammengefasst werden müssen.
- In der Wechselstromtechnik besagt der Maschensatz, dass die Augenblickwerte der Wechselspannungen zusammengefasst werden müssen.
Spannungszeiger – Vorgehensweise
Da wir ja bereits erkannt haben, dass die Ermittlung von Summenspannungen mit dem Zeigerdiagrammen viel einfacher von der Hand geht, befassen wir uns in diesem Kurstext nur noch mit Zeigern.
Spannungszeiger – Rotierende Spannungszeiger
Stellen wir uns einen Schaltplan mit einer Wechselstromschaltung vor, genauer gesagt einen Ausschnitt davon. Hier liegen zwei Widerstand in Reihenschaltung vor.
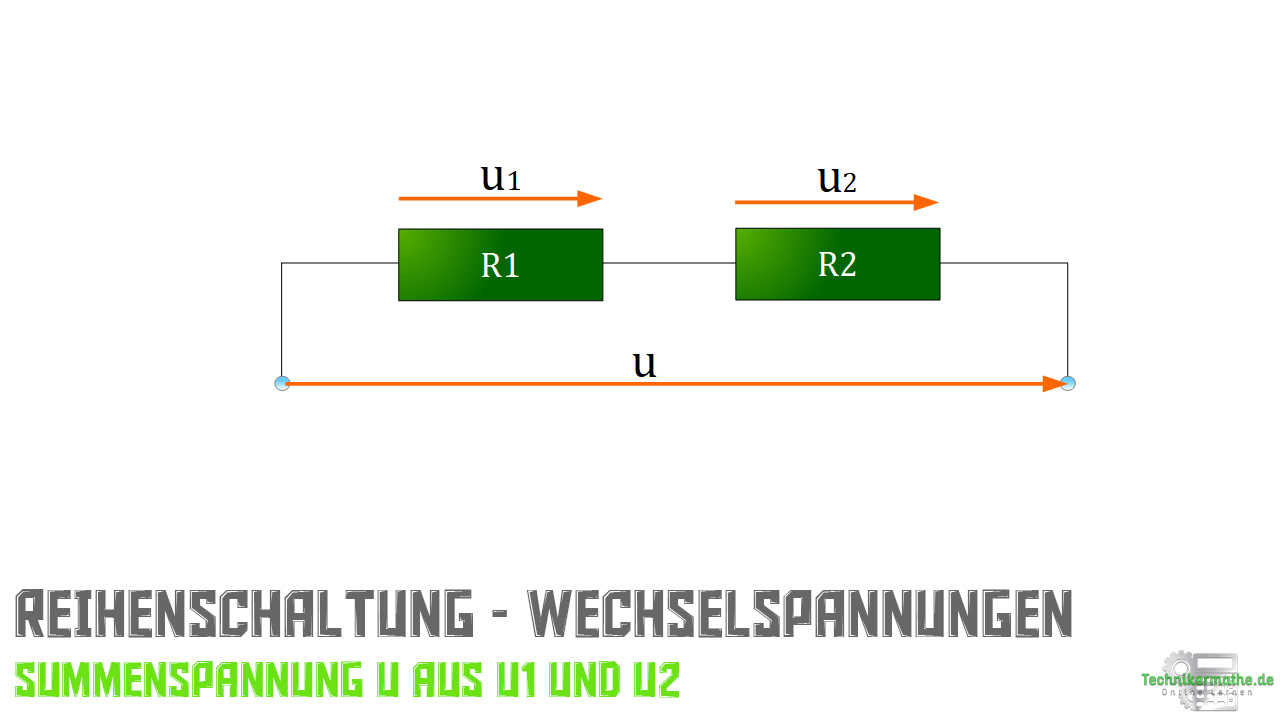
Die anliegenden Wechselspannungen sind sinusförmige mit einer gleichen Frequenz und Effektivwerten.
Die Effektivwerte ![]() und
und ![]() werden mit Hilfe von Zählpfeilen
werden mit Hilfe von Zählpfeilen ![]() und
und ![]() dargestellt.
dargestellt.
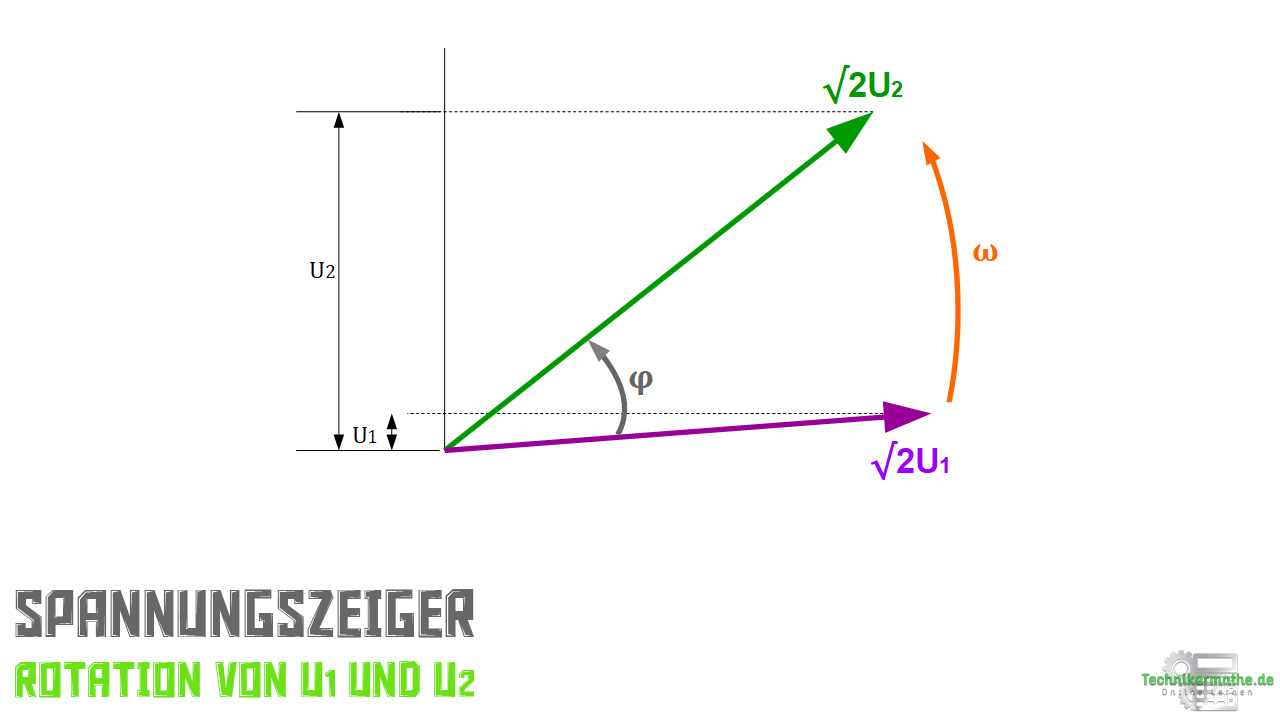
Der Abbildung kannst du entnehmen, dass die rotierenden Spannungszeiger um den Winkel ![]() gegeneinander versetzt sind. Die Winkelgeschwindigkeit
gegeneinander versetzt sind. Die Winkelgeschwindigkeit ![]() ist bei beiden konstant.
ist bei beiden konstant.
Spannungszeiger – Projektion
Ausgehend vom Maschensatz ist es uns jetzt möglich den Effektivwert von ![]() sowie den Winkel der
sowie den Winkel der ![]() der Wechselspannung
der Wechselspannung ![]() zu bestimmen.
zu bestimmen.
Du erinnerst dich? – Die Maschenregel besagt bei Wechselspannungen
![]()
Für die beiden Zeiger ![]() und
und ![]() haben wir die Augenblickwerte
haben wir die Augenblickwerte ![]() und
und ![]() zu einem beliebigen Zeitpunkt gegeben. Jetzt können wir, wie in der nächsten Abbildung dargestellt, die jeweiligen Zeiger mit Hilfe einer Parallelverschiebung mit deren Ende an die Spitze des jeweils anderen Zeigers legen.
zu einem beliebigen Zeitpunkt gegeben. Jetzt können wir, wie in der nächsten Abbildung dargestellt, die jeweiligen Zeiger mit Hilfe einer Parallelverschiebung mit deren Ende an die Spitze des jeweils anderen Zeigers legen.
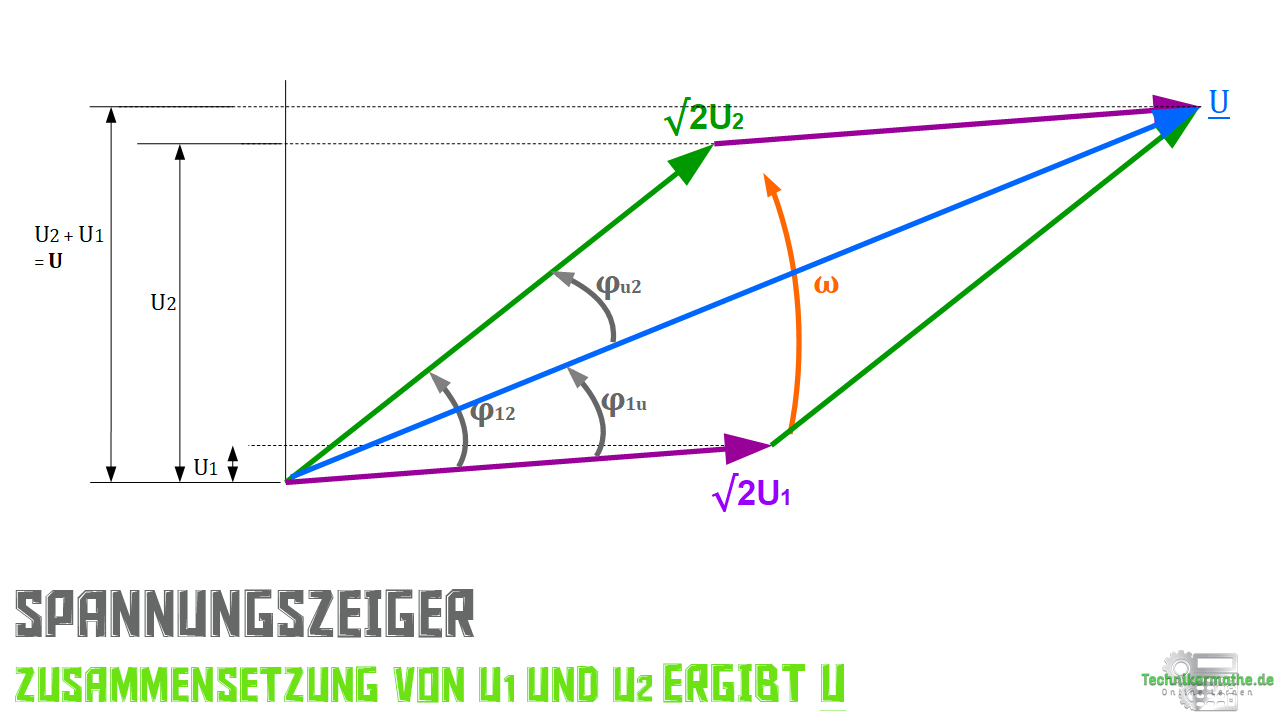
Wenn richtig gezeichnet wurde verläuft die Summenspannung ![]() vom Ursprung bis zur Spitze der beiden parallelverschobenen Zeiger. Damit haben wir den resultierenden Spannungszeiger bestimmt, den wir als neuen Effektivwert ablesen können. Gleiches gilt für die neu entstandenen Winkel
vom Ursprung bis zur Spitze der beiden parallelverschobenen Zeiger. Damit haben wir den resultierenden Spannungszeiger bestimmt, den wir als neuen Effektivwert ablesen können. Gleiches gilt für die neu entstandenen Winkel ![]() und
und ![]() , die wir ebenfalls ablesen können.
, die wir ebenfalls ablesen können.
In der Literatur findest du häufig in Bezug auf die Spannungszeiger folgende Gleichung:
![]()
Da die Spannungszeiger analog zur Kräftebestimmung in der Technische Mechanik in Hinblick auf Betrag und Richtung richtig berücksichtigt werden müssen, nutzt man in Schaltplänen anstelle der Angabe der Zählpfeile ![]() und
und ![]() die Zeiger
die Zeiger ![]() und
und ![]()
Spannungszeiger – Berechnung des Effektivwerts und Winkels
Da wir nun alle Größen zeichnerisch ermittelt haben, machen wir uns jetzt ans Werk und stellen Gleichungen zur Berechnung des Effektivwerts und des Winkels auf:
Effektivwert:![]()
Winkel: ![]()
Stromzeiger – Vorgehensweise
Da wir ja bereits erkannt haben, dass die Ermittlung von Summenströmen mit dem Zeigerdiagrammen viel einfacher von der Hand geht, befassen wir uns auch hier nur noch mit Zeigern.
Stromzeiger – Rotierende Stromzeiger
Stellen wir uns einen Schaltplan mit einer Wechselstromschaltung vor, genauer gesagt einen Ausschnitt davon. Hier liegen zwei Widerstand als Parallelschaltung vor.
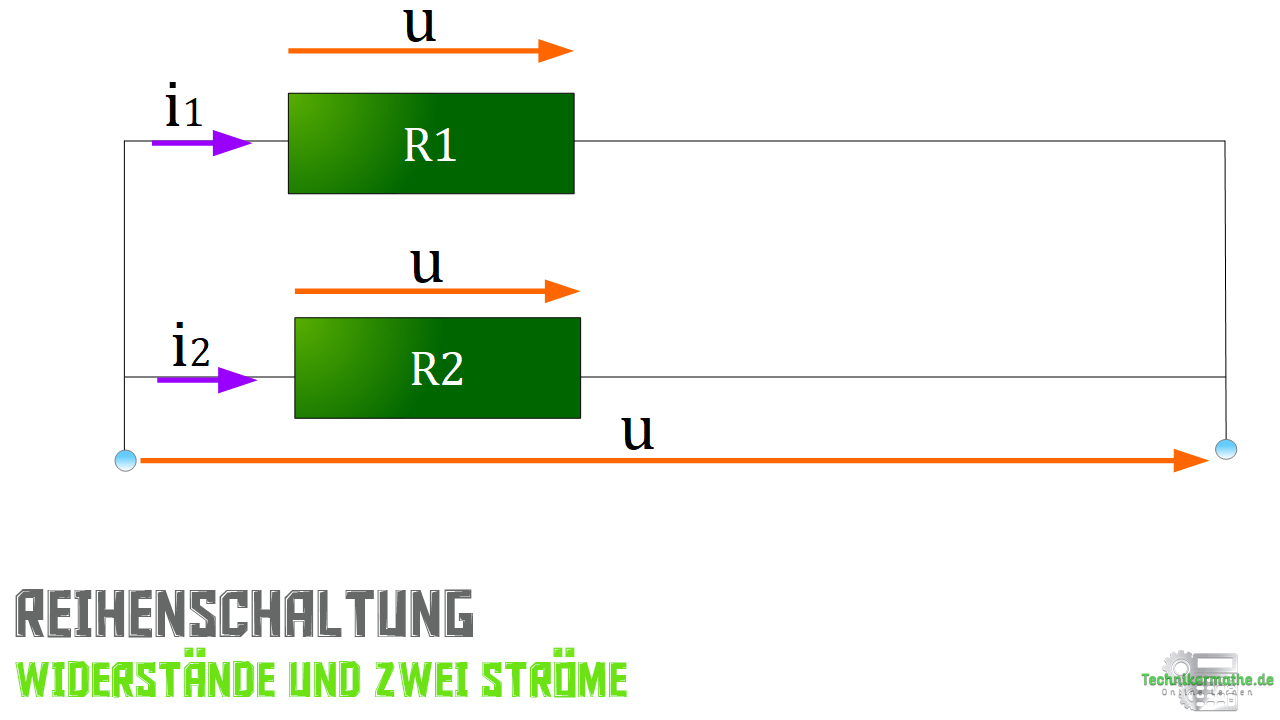
Die anliegenden Wechselströme sind sinusförmige mit einer gleichen Frequenz und Effektivwerten.
Die Effektivwerte ![]() und
und ![]() werden mit Hilfe von Zählpfeilen
werden mit Hilfe von Zählpfeilen ![]() und
und ![]() dargestellt.
dargestellt.
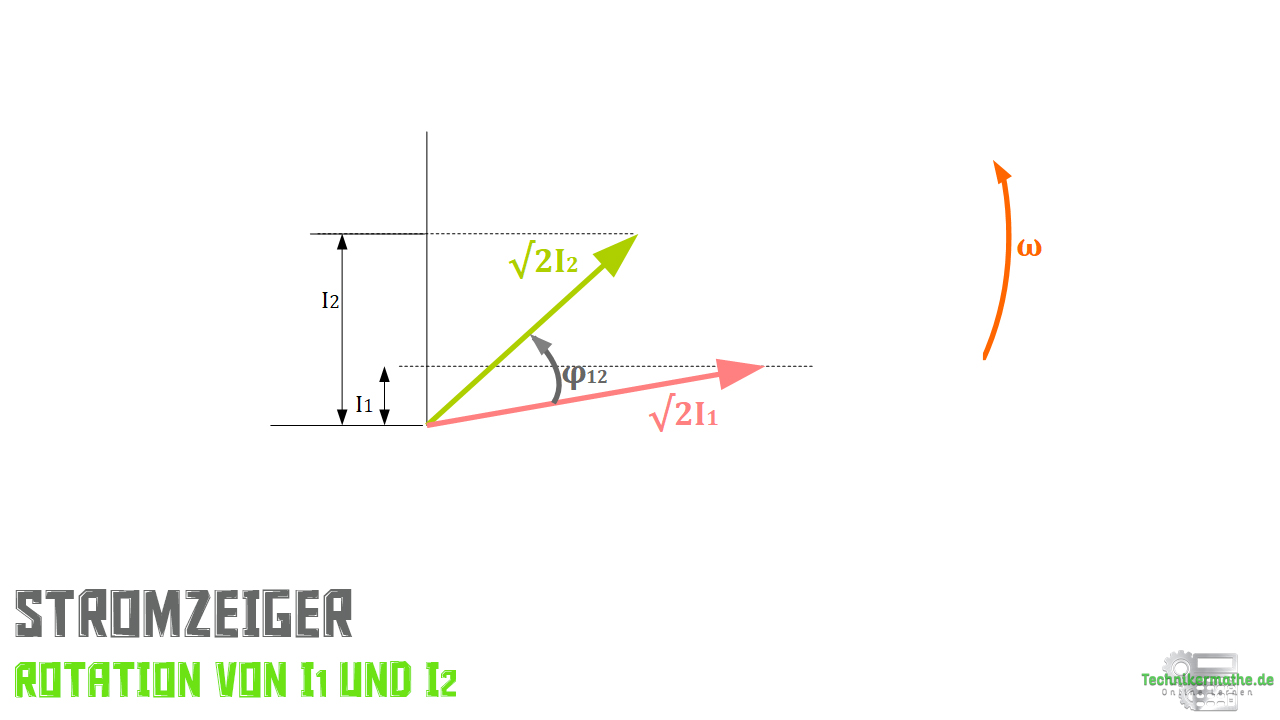
Der Abbildung kannst du entnehmen, dass die rotierenden Stromzeiger um den Winkel ![]() gegeneinander versetzt sind. Die Winkelgeschwindigkeit
gegeneinander versetzt sind. Die Winkelgeschwindigkeit ![]() ist bei beiden konstant.
ist bei beiden konstant.
Stromzeiger – Projektion
Ausgehend vom Knotensatz ist es uns jetzt möglich den Effektivwert von ![]() sowie den Winkel der
sowie den Winkel der ![]() des Wechselstroms
des Wechselstroms ![]() zu bestimmen.
zu bestimmen.
Der Knotensatz besagt bei Wechselströmen
![]()
Für die beiden Zeiger ![]() und
und ![]() haben wir die Augenblickwerte
haben wir die Augenblickwerte ![]() und
und ![]() zu einem beliebigen Zeitpunkt gegeben. Jetzt können wir, wie in der nächsten Abbildung dargestellt, die jeweiligen Zeiger mit Hilfe einer Parallelverschiebung mit deren Ende an die Spitze des jeweils anderen Zeigers legen.
zu einem beliebigen Zeitpunkt gegeben. Jetzt können wir, wie in der nächsten Abbildung dargestellt, die jeweiligen Zeiger mit Hilfe einer Parallelverschiebung mit deren Ende an die Spitze des jeweils anderen Zeigers legen.
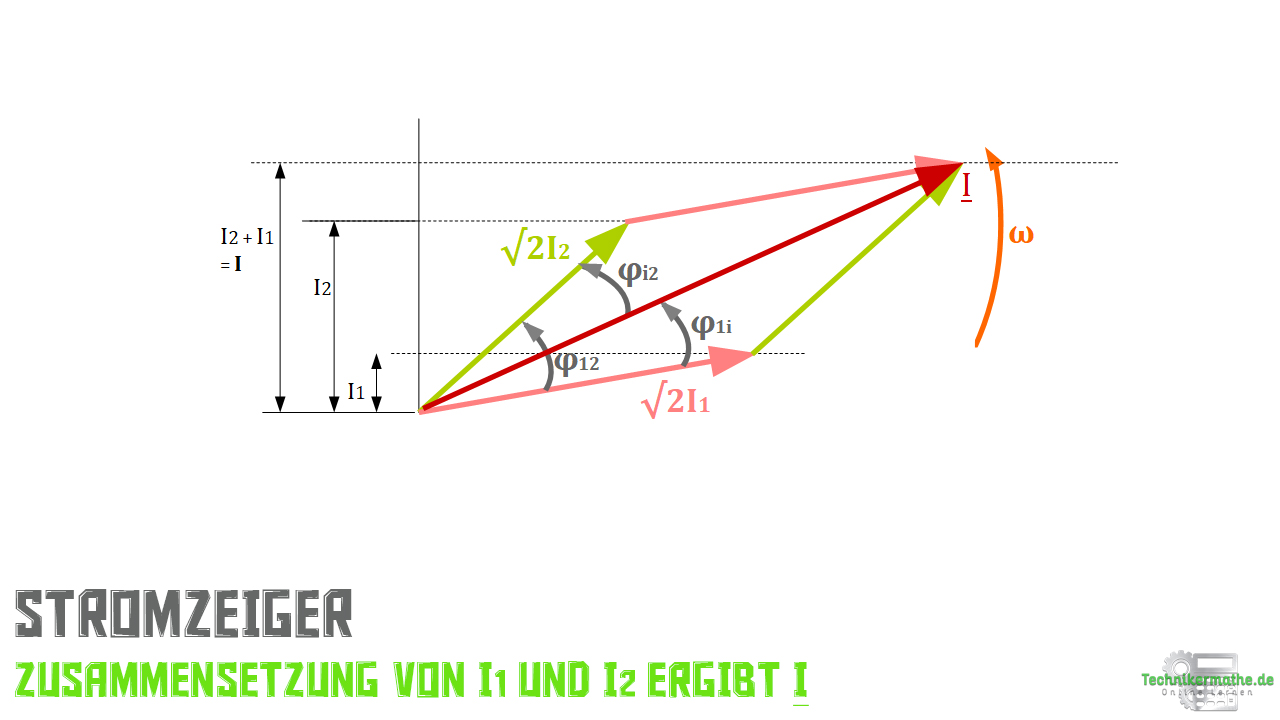
Wenn richtig gezeichnet wurde verläuft der Summenstrom ![]() vom Ursprung bis zur Spitze der beiden parallelverschobenen Zeiger. Damit haben wir den resultierenden Stromzeiger bestimmt, den wir als neuen Effektivwert ablesen können. Gleiches gilt für die neu entstandenen Winkel
vom Ursprung bis zur Spitze der beiden parallelverschobenen Zeiger. Damit haben wir den resultierenden Stromzeiger bestimmt, den wir als neuen Effektivwert ablesen können. Gleiches gilt für die neu entstandenen Winkel ![]() sowie
sowie ![]() , auch diese können wir genau ablesen.
, auch diese können wir genau ablesen.
In der Literatur findest du häufig in Bezug auf die Stromzeiger folgende Gleichung:
![]()
Da die Stromzeiger analog zur Kräftebestimmung in der Technische Mechanik in Hinblick auf Betrag und Richtung richtig berücksichtigt werden müssen, nutzt man in Schaltplänen anstelle der Angabe der Zählpfeile ![]() und
und ![]() die Zeiger
die Zeiger ![]() und
und ![]() [/intense_content_box]
[/intense_content_box]
Stromzeiger – Berechnung des Effektivwerts und Winkels
Da wir nun alle Größen zeichnerisch ermittelt haben, machen wir uns jetzt ans Werk und stellen Gleichungen zur Berechnung des Effektivwerts und des Winkels auf:
Effektivwert: ![]()
Winkel: ![]()
Nachdem wir jetzt das Thema Zeigerbilder behandelt haben und du ein Gefühl dafür bekommst hast wie die erwähnten Strom– und Spannungszeiger erstellt und genutzt werden, möchten wir in der kommenden Lerneinheit noch mal intensiv auf sinusförmige Spannung und Ströme eingehen. Damit schaffen wir dann die Grundvoraussetzung für die kommenden Berechnungen zu Wechselstromkreisen.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






