(ET5-046) – Leistung und Arbeit [Wirk-, Blind-, Schein-]

In diesem Kurstext erlernst du alles Relevante zum Thema Leistung und Arbeit in der Wechselstromtechnik. Du erlernst alles zu

Wirkleistung,
Blindleistung,
Scheinleistung

sowie

Wirkarbeit,
Blindarbeit und
Scheinarbeit.

Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET6-Wechselstromtechnik 1

Die Vertiefung der Wechselstromtechnik findest du im Kurs: ET7-Wechselstromtechnik 2

Merk’s dir!

In der Wechselstromtechnik ist die Leistung die Fähigkeit eines Systems, Arbeit zu verrichten oder Energie pro Zeiteinheit umzuwandeln. Sie wird in der Regel in der Einheit Watt gemessen.

Die Leistung in einem Wechselstromsystem kann durch verschiedene Faktoren beeinflusst werden, darunter die Spannung, der Strom und der Phasenwinkel zwischen ihnen. In einem rein ohmschen Wechselstromkreis ist die Leistung das Produkt aus der effektiven Spannung und dem effektiven Strom, multipliziert mit dem Cosinus des Phasenwinkels zwischen Spannung und Strom.

Dieser Wert wird als Scheinleistung bezeichnet und hat eine wichtige Rolle bei der Beurteilung der Effizienz und Leistungsfähigkeit von elektrischen Systemen.

Leistung im Wechselstrom – Grundlagen

Leistung - Blindleistung, Wirkleistung, Scheinleistung — Wechselstromtechnik – Leistung – Blindleistung, Wirkleistung, Scheinleistung

Die Leistung kann in der Wechselstromtechnik unterschiedliche Formen annehmen und wird entsprechend auch unterschiedlich bewertet. Auch hier unterscheiden wir wieder zwischen einem Widerstandes (Wirkleistung) sowie Spulen und Kondensatoren (Blindleistungen), sowie die Kombination aus beiden als Scheinleistung. Zum Ende hin stellen wir dir noch den Leistungsfaktor vor.

Formeln zur Bestimmung der Leistung

Nachfolgend stellen wir dir die grundlegenden Gleichungen der Leistung in der Wechselstromtechnik vor.

Allgemeine Gleichungen

Um in der Wechselstromtechnik diese Größe zu bestimmen, bedienen wir uns der allgemeinen Gleichung für die Leistung und passen diese für den Augenblickswert an. Hierzu benötigen wir die Angabe von Spannung und Strom.

$P = U \cdot I$ – Allgemeine Gleichung für P

$P_t = u \cdot i$ – Angepasste Gleichung für den Augenblickwert von P

Zeitfunktionen

Hinzu kommen, die dir bereits vertrauten Gleichungen für die Zeitfunktionen von Spannung und Strom:

$u = \sqrt{2} \cdot U \cdot sin(\omega t + \varphi_u)$ Zeitfunktion der Spannung

$i = \sqrt{2} \cdot I \cdot sin(\omega t + \varphi_i)$ Zeitfunktion des Stroms

Mathematische Beziehungen

Für die weitere Berechnung gehen wir in die und stellen folgende Beziehungen auf

$sin \alpha \cdot sin \beta = \frac{1}{2} [cos (\alpha - \beta) - cos (\alpha + \beta)$

$\varphi = \varphi_u - \varphi_i$

Diese Gleichungen setzen wir in unsere Gleichung für die Augenblickwerte ein und erhalten daraufhin im ersten Schritt:

$P_t = u \cdot i = (\sqrt{2} \cdot U \cdot sin(\omega t + \varphi_u)) \cdot (\sqrt{2} \cdot I \cdot sin(\omega t + \varphi_i))$

Angepasst erhalten wir dann:

$P_t = 2 \cdot U \cdot I \cdot \frac{1}{2} \cdot ( \varphi - cos(2\cdot \omega \cdot t + \varphi_u + \varphi_i))$

Im letzten Schritt multiplizieren wir die Gleichung dort wo es möglich ist aus und erhalten:

$P_t = U \cdot I \cdot \varphi - U \cdot I \cdot cos (2\omega \cdot t + \varphi_u + \varphi_i)$

Die verkürzte Form ist:

Finale Gleichungen

$P_t = P - P_{\sim}$

mit

$P =U \cdot I \cdot \varphi$ Leistung

sowie

$P_{\sim} = U \cdot I \cdot cos (2\omega \cdot t + \varphi_u + \varphi_i)$ Wechselanteil von P

Formen der Leistung im Wechselstrom – Überblick

Jetzt stellen wir dir einfach und unkompliziert die einzelnen Formen nacheinander vor.

In der Gleichstromtechnik genügt uns die Gleichung

$P = U \cdot I$ .

Hingegen in der Wechselstromtechnik berücksichtigen wir zusätzlich den Phasenverschiebungswinkel mit

$P = U \cdot I \cdot cos \varphi$ .

Wirkleistung P

“Die Wirkleistung ist der Realteil der Scheinleistung.”

$P = Re(S)$

Die $P$ ist der Teil der Leistung, welcher aus wirklich geleistet wird. Dabei geht es um die Umwandlung in eine andere Energieform, wie Wärme oder Licht, bzw. mechanische Energie.

Liegt ein rein ohm’scher Verbraucher vor, so entspricht die 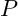$P$ exakt der Scheinleistung, weshalb der Phasenverschiebungswinkel zwischen Strom und Spannung gleich null wird.

$\varphi = 0$

Liegt ein normaler ohm’scher Verbraucher vor, so entspricht die 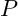$P$ nicht der Scheinleistung, da hier noch die Blindleistung berücksichtigt werden muss. Der Phasenverschiebungswinkel ist hier nicht null.

$\varphi \not= 0$

Und das bedeutet…

Die Größe tritt in induktiver und kapazitiver Form auf.

Formel + Einheit

Berechnung mit S und Phasenverschiebungswinkel – Formel + Einheit

Hast du die Scheinleistung und den Phasenverschiebungswinkel gegeben, so kannst du damit auch $P$ berechnen. Diese Größe errechnet sich hier mit dem Kosinussatz wie folgt:

$P = S \cdot cos(\varphi)$

Kennzahlen:

$S =$ Scheinl.

$P =$ Wirkl.

$\varphi =$ Phasenverschiebungswinkel

$cos(\varphi) =$ L.faktor

Einheit:

Die Angabe der Größe erfolgt in Volt-Ampere (VA)

Berechnung mit Effektivwert von Strom und Spannung – Formel + Einheit

Die Scheinleistung kann auch unter Kenntnis von den Effektivwerten des Stroms und der Spannung errechnet werden. Hier nimmst du immer die Beträge der Effektivwerte für deine Berechnung:

$P = U \cdot I \cdot cos(\varphi)$

Kennzahlen:

$S =$ Scheinl.

$U =$ Effektivwert der Spannung

$I =$ Effektivwert des Stroms

$cos(\varphi) =$ L.faktor

Einheit:

Die Angabe der Größe erfolgt in Watt [W]

Blindleistung Q

“Die Blindleistung ist der Imaginärteil der Scheinleistung.”

$Q = Im(S)$

So ist $Q$ ist der Teil von $S$ , der periodisch zwischen elektrischer Quelle und dem Verbraucher hin und her bewegt wird. Sie hat keinen Einfluss auf die Energieerzeugung, also die Umwandlung in andere Energieformen, im Verbraucher und leistet entsprechend auch keinen Beitrag dazu.

Diese Größe entsteht aufgrund der Phasenverschiebung von Strom und Spannung.

Erinnerst du dich?…

In Wechselstromkreisen existieren keine idealen Verbraucher. Diese haben immer einen Wirkanteil aber auch einen Blindanteil. Wobei letzterer entweder eine induktive (wie Spulen) oder eine kapazitive (wie Kondensatoren) Erscheinung hat. Wird der Wert von $Q$ negativ, so bedeutet diese, dass zu diesem Zeitpunkt Leistung von dem Verbraucher wieder an die elektrische Quelle angegeben wird.

Berechnung mit S und Phasenverschiebungswinkel – Formel + Einheit

Wir können die $Q$ mit Hilfe unseres Zeigerdiagramms ermitteln:

$Q = S \cdot sin{\varphi}$

Kennzahlen:

$Q =$ Blindl.

$S =$ Scheinl.

$\varphi =$ Phasenverschiebungswinkel

Einheit:

Die Angabe der Größe erfolgt in Volt-Ampere-reactive [VA]

Berechnung mit Spannung und Strom und Phasenverschiebungswinkel – Formel + Einheit

Alternativ können wir die Größe $Q$ auch mit Kenntnis von Spannung und Strom ermitteln. Wobei wenn du aufgepasst hast, dann hast du schon gemerkt, dass $S$ ja das Produkt aus $U$ und $I$ nach dem Zeigerdiagramm ist.

$Q = U \cdot I \cdot sin{\varphi}$

Kennzahlen:

$Q =$ Blindl.

$U =$ Effektivwert der Spannung

$I =$ Effektivwert des Stroms

$\varphi =$ Phasenverschiebungswinkel

Die Größe Q besteht aus zwei Teilen. Ein Teil ist die induktive Blindleistung $Q_L$ und der andere Teil ist die kapazitive Blindleistung $Q_C$ . In den meisten Berechnungen gibt mal die Betragswerte von beiden um den Gesamtwert zu bestimmen.

$|Q|= |Q_L|- |Q_C|$

Scheinleistung S

“Die Scheinleistung setzt sich aus der Wirkl. und der Blindl. zusammen.”

Es ist die Größe, die eine elektrische Quelle in einem Wechselstromkreis einem Verbraucher zur Verfügung stellt.

Fassen wir noch mal zusammen:

“Die Wirkl. ist der Realteil der Scheinleistung.”

“Die Blindl. ist der Imaginärteil der Scheinleistung.”

Also gilt : = +

Der Schein trügt… nicht!…

Die Scheinleistung ist genau der Wert, mit dem das Stromnetz belastet wird. Daher muss bei der Auslegung des Stromnetzes immer von der $S$ und nicht von der $P$ ausgegangen werden.

Berechnung mit P und Q – Formel + Einheit

Hast du die $P$ und die $Q$ gegeben, so kannst du damit die Scheinleistung berechnen. Diese Größe errechnet sich hier mit dem Satz des Pythagoras wie folgt:

$S = \sqrt{(P^2 + Q^2)}$

Kennzahlen:

$S =$ Scheinl.

$P =$ Wirkl.

$Q =$ Blindl.

Einheit:

Die Angabe der Wirkleistung erfolgt in Volt-Ampere (VA)

Berechnung mit Effektivwert von Strom und Spannung – Formel + Einheit

Die Scheinleistung kann auch unter Kenntnis von den Effektivwerten des Stroms und der Spannung errechnet werden. Hier nimmst du immer die Beträge der Effektivwerte für deine Berechnung:

$S = U \cdot I$

Kennzahlen:

$S =$ Scheinl.

$U =$ Effektivwert der Spannung

$I =$ Effektivwert des Stroms

In einem vorherigen Kurstext hast du bereits die Impedanz $Z$ kennengelernt. Diese Hilft dir jetzt auch bei der Berechnung der Scheinleistung. Denn es gilt:

$S = I^2 \cdot Z$

sowie

$S = \frac{U^2}{Z}$

Merk’s dir!

Liegt uns eine komplexe Darstellung vor, so können wir wie gewohnt unser Zeigerdiagramm nutzen und zusätzlich den Phasenverschiebungswinkel bestimmen.

Leistungsfaktor

Der Leistungsfaktor $\lambda$ gibt uns Auskunft über das Verhältnis von Wirkleistung zu Scheinleistung eines Verbrauchers im Wechselstromkreis. Der Faktor ist also eine Verhältniszahl.

$\lambda = cos(\varphi) =$ Leistungsfaktor

Merk’s dir!

Erreicht der Faktor einen Wert von 1, so tritt im Wechselstromkreis keine Blindleistung auf. Da eine Blindleistung unerwünscht ist weil sie zu einer Mehrbelastung des Wechselstromkreises führt, versucht man den Faktor bis an den Wert 1 heranzuführen.

Leistungsfaktor - Herstellerangabe aus Angabe der Wirkleistungsaufnahme — Leistungsfaktor – Herstellerangabe aus Angabe der Wirkleistungsaufnahme

Übrigens ist der Leistungsfaktor ein gutes Maß zur Beurteilung der Gewichtung der Anteile von P und Q an S.

Hersteller geben den Faktor an um Aussagen über die Wirkleistungsaufnahme zu treffen. Du findest diese Angabe auf dem Typenschild.

Berechnung mit P und S – Formel + Einheit

$\lambda = \cos(\varphi) = \frac{P}{S}$

Der Faktor ist eine dimensionslose Größe.

Arbeit im Wechselstrom – Grundlagen

Arbeit im Wechselstromkreis (Wirkarbeit, Blindarbeit, Scheinarbeit)

Werden Ladungsträger durch Einfluss einer elektrischen Spannung $U$ mit einer Elektrizitätsmenge $Q$ bewegt, so erfolgt die Verrichtung einer Arbeit.

Diese elektrische Arbeit lassen sich Energieversorger von dir bezahlen. Wenn du also das nächste Mal deine Stromrechnung in den Händen hältst und darauf Stromverbrauch steht, dann ist damit die elektrische Arbeit gemeint.

So wie oben definieren wir auch bei der Arbeit die unterschiedlichen Formen. Hierzu schauen wir uns die Gleichungen zur Wirkarbeit, Blindarbeit und Scheinarbeit detailliert an. Die obigen Gleichungen helfen dabei die Gleichungen für die unterschiedlichen Formen der Arbeit zu erstellen.

“Die Arbeit ist das Produkt aus Leistung $P$ und Zeitdauer $t$ ” – Das gilt sowohl für die Gleichstromtechnik, als auch für die Wechselstromtechnik.

Berechnung der Arbeit mit Spannung, Strom, Elektrizitätsmenge und Zeit

Jedoch kannst du die elektrische Arbeit auch über einen anderen Weg errechnen.

$W = Q \cdot U$

Kennzahlen:

$W =$ – Elektrische Arbeit

$Q =$ – Elektrizitätsmenge

$U =$ – Spannung

Dabei errechnet sich die Elektrizitätsmenge $Q$ mit:

$Q = I \cdot t$

Kennzahlen:

$Q =$ – Elektrizitätsmenge

$I =$ – Elektrischer Strom

$t =$ – Zeiteinheit

Somit können wir unsere Gleichung anpassen und erhalten

$W = U \cdot I \cdot t$

Kennzahlen:

$W =$ – Elektrische Arbeit

$I =$ – Elektrischer Strom

$U =$ – Spannung

$t =$ – Zeiteinheit

Womit wir wieder bei der Relation zwischen elektrischer Arbeit und elektrischer Leistung angekommen wären.

$W = U \cdot I \cdot t = P \cdot t$

Davon ausgehend folgen nun die drei relevanten Gleichungen.

Formen der Arbeit im Wechselstrom – Überblick

Nachfolgend findest du die Gleichungen zur Berechnung der elektrischen Arbeit für die unterschiedlichen Typen:

Berechnung der Wirkarbeit – Formel + Einheit

Die Wirkarbeit errechnet sich aus dem Produkt von Wirkleistung und Zeiteinheit:

$W = P \cdot t = (U \cdot I \cdot cos \varphi) \cdot t$

Die Angabe der Wirkarbeit erfolgt im der Einheit Watt Sekunde (Ws).

Berechnung der Blindarbeit – Formel + Einheit

Die Blindarbeit errechnet sich aus dem Produkt von Blindleistung und Zeiteinheit:

$W_q = Q \cdot t = (U \cdot I \cdot sin\varphi) \cdot t$

Die Angabe der Blindarbeit erfolgt im der Einheit Watt Sekunde (Ws).

Berechnung der Scheinarbeit – Formel + Einheit

Die Scheinarbeit errechnet sich aus dem Produkt von Scheinarbeit und Zeiteinheit:

$W_s = S \cdot t = (U \cdot I \cdot) \cdot t}$

Die Angabe der Scheinarbeit erfolgt im der Einheit Watt Sekunde (Ws).

Lernclip – P & W – zusammenfassender Überblick

Was kommt als Nächstes?

Nachdem wir ausführlich dieses Thema behandelt haben, stellen wir dir in der nächsten Kurseinheit die Kirchhoff’schen Gesetze im Zusammenhang mit der Wechselstromtechnik ausführlich vor.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++