(ET5-045) – Phasenverschiebungswinkel

In diesem Kurstext erklären wir dir ganz einfach und unkompliziert was der Phasenverschiebungswinkel φ ist. Dabei stellen wir dir den Phasenverschiebungswinkel für die Größen von

Wirk- und Blindwiderständen

sowie

Wirk- und Blindleitwerten

in Reihen- und Parallelschaltungen vor.

Phasenverschiebungswinkel – Grundlagen

Der Phasenverschiebungswinkel, in der Literatur häufiger auch Phasenwinkel genannt, gibt uns die Auskunft über die Phasenlage der anliegenden Spannung der Schaltung und dem Gesamtstrom.

Liegt eine Reihenschaltung vor, so wird dem Strom als Bezugsgröße der Winkel $\varphi = 0°$ zugeordnet.

Liegt ein Spannungsdreieck vor, so wird die Phasenlange von dem zwischen Gesamtspannung an der Impedanz Z und der Wirkspannung an R auftretenden Winkel bestimmt.

Liegt ein Widerstandsdreieck vor, so wird der Winkel zwischen dem Impedanzszeiger und dem Wirkwiderstandszeiger als Phasenwinkel gewählt.

Die Tangensfunktion des Phasenwinkels ergibt sich aus dem Verhältnis von Gegenkathete zur Ankathete. Hier errechnet sich der Winkel aus der Umkehrfunktion. Die Umkehrfunktion ist der Arcustangens.

Phasenverschiebungswinkel – Schaltungsvarianten

In den nachfolgenden Betrachtung gehen wir immer von einer Betriebspannung mit sinusförmigen Verlauf aus.

Merk's dir!

Wir untersuchen zumeist das Verhalten von Schaltelementen in einer Reihen- oder Parallelschaltung und berechnen dabei oft den Gesamtwiderstand. Die Tatsache, dass sich Wirkwiderstände und Blindwiderstände unterschiedlich im Wechselstromkreis verhalten, sollten wir hier berücksichtigen.

Wie du bereits weißt, stellt der Scheinwiderstand den Gesamtwiderstand dieser Schaltung dar. Auch, dass man ihn als Impedanz bezeichnet, sollte dir bereits geläufig sein. Wenn wir Größen berechnen müssen, so bedienen wir uns des Ohm’schen Gesetzes.

undefiniert

Mal so, mal so

Der Scheinwiderstand (Impedanz) errechnet sich aus dem Messwerten von anliegender Spannung und resultierenden Gesamtstrom. Dabei fällt auf, dass sich der Spannungswert immer proportional zur Impedanz verhält.

Anders verhält es sich beim Scheinleitwert. Dieser errechnet sich aus dem Kehrwert des Scheinwiderstandes und verhält sich proportional zum Gesamtstrom.

Wir untersuchen jetzt unterschiedliche Kombinationen aus Wirk- und Blindwiderständen an einer Sinusspannung in Hinblick auf dem Phasenverschiebungswinkel:

RC-Reihenschaltung

sowie

RL-Reihenschaltung

sowie

RCL-Reihenschaltung

sowie

RC-Parallelschaltung

sowie

RL-Parallelschaltung

sowie

RCL-Parallelschaltung

Jede dieser Schaltungsvarianten betrachten und berechnen wir in einem späteren Kursabschnitt nochmals detailliert.

Phasenverschiebungswinkel – Grafik – Übersicht

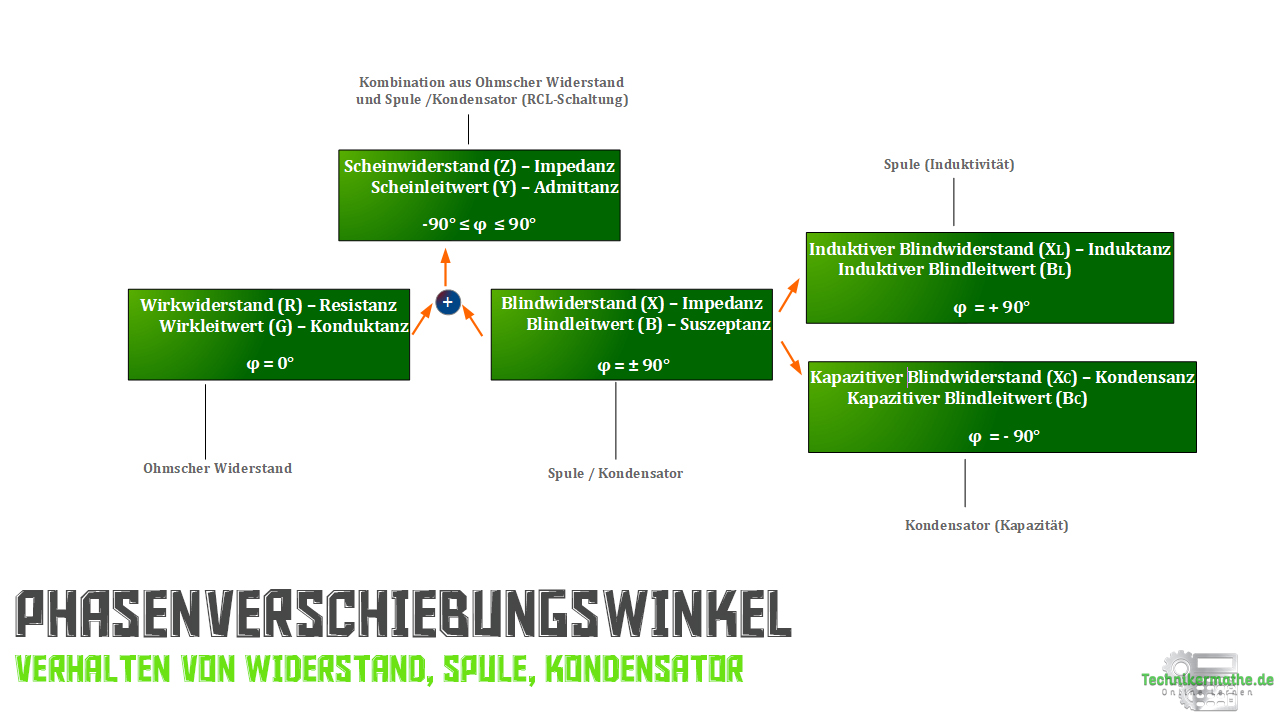
In der nächsten Abbildung siehst du eine Übersicht von Wechselstromwiderständen und Wechselstromleitwerten, in Hinblick auf Wirkwiderstände und Blindwiderstände sowie die Angabe des Phasenverschiebungswinkels. Alternativ spricht man bei der Übersicht von einem Stammbaum.

Hier wurde der Strom als Bezugsgröße mit der Phasenlage von 0° festgelegt.

Phasenverschiebungswinkel – Zeigerdiagramm

Wir betrachten ja immer Wirkwiderstände und Blindwiderstände. Aus diesem Grund trennen wir auch die x-Achse von der y-Achse.

Außerdem solltest du dir merken:

Ein Zeiger beginnt zweckmäßig im Koordinatennullpunkt.
Der Umlaufsinn der Zeiger von Strom und Spannung ist immer gegen den Uhrzeigersinn gerichtet.
Der Drehwinkel ist bei einer Linksdrehung positiv und geht bei einer Drehung im Zurzeigersinn mit einem negativen Vorzeichen in Berechnungen ein.

X-Achse – Wirkwiderstände

In Zeigerdiagrammen ist die x-Achse mit den Wirkanteilen (Wirkwiderständen) verbunden, weshalb sie als reelle Achse bezeichnet wird.

Liegt uns ein Ohmscher Widerstand, besser gesagt ein Wirkwiderstand vor, so wissen wir automatisch, dass der Strom und die Spannung zueinander phasengleich sind. Der Phasenverschiebungswinkel ist somit:

$\boxed{ \varphi = 0° }$ – Wirkwiderstände

Y-Achse – Blindwiderstände

Auf der y-Achse, es handelt sich um die vertikale Achse, trägt man die Blindkomponenten (Blindwiderstände) ab. So ist bei allen Blindgrößen, der Phasenverschiebungswinkel zwischen dem Strom und der Spannung exakt:

$\boxed{ \varphi = \pm 90° }$ – Blindwiderstände

Jede Wechselstromgröße kann von uns in seine Wirkkomponenten und Blindkomponenten zerlegt werden.

Diese Zerlegung ist zulässig, da ideale Baugruppen nicht existieren.

Sind dir die Frequenz und die Einzelgrößen von Widerstand, Spule und Kondensator bekannt, so kannst du mit den Zeigerdiagramme viele Aussagen über die Gesamtschaltung hinsichtlich Verhalten und Eigenschaft treffen.

Im rechtwinkligen Koordinatensystem ist ein Zeiger charakterisiert durch seine Länge und den Winkel, den er mit der horizontalen x-Achse bildet. Jeder Zeiger kann in der Darstellungsebene unter Beibehaltung seiner Eigenschaften parallel zur x- und y-Achse verschoben werden.

Phasenverschiebungswinkel – Kombinationen

Jetzt stellen wir dir die Phasenverschiebungswinkel vor, so wie sie bei den oben aufgelisteten Kombinationen aus Wirk- und Blindwiderständen auftreten.

Phasenwinkel – RC-Reihenschaltung

Der Phasenwinkel des Stromzeigers beträgt $\varphi = 0 °$

Das ist darin begründet, dass es sich um eine Reihenschaltung handelt und der Strom überall gleich ist. Daher wählt man den Strom als Bezugsgröße und den Stromzeiger als Bezugsgröße in Richtung der x-Achse.

R-Element (Ohmscher Wirkwiderstand): Spannung und Strom liegen in Phase

$\boxed{ \rightarrow \varphi = 0° }$

C-Element ( Kapazitiver Blindwiderstand [Kondensator]): Spannung läuft dem Strom mit dem Phasenwinkel

$\boxed{ \rightarrow \varphi = -90° }$

nach.

Grafische Ermittlung

In der nächsten Abbildung findest du eine typische RC-Reihenschaltung:

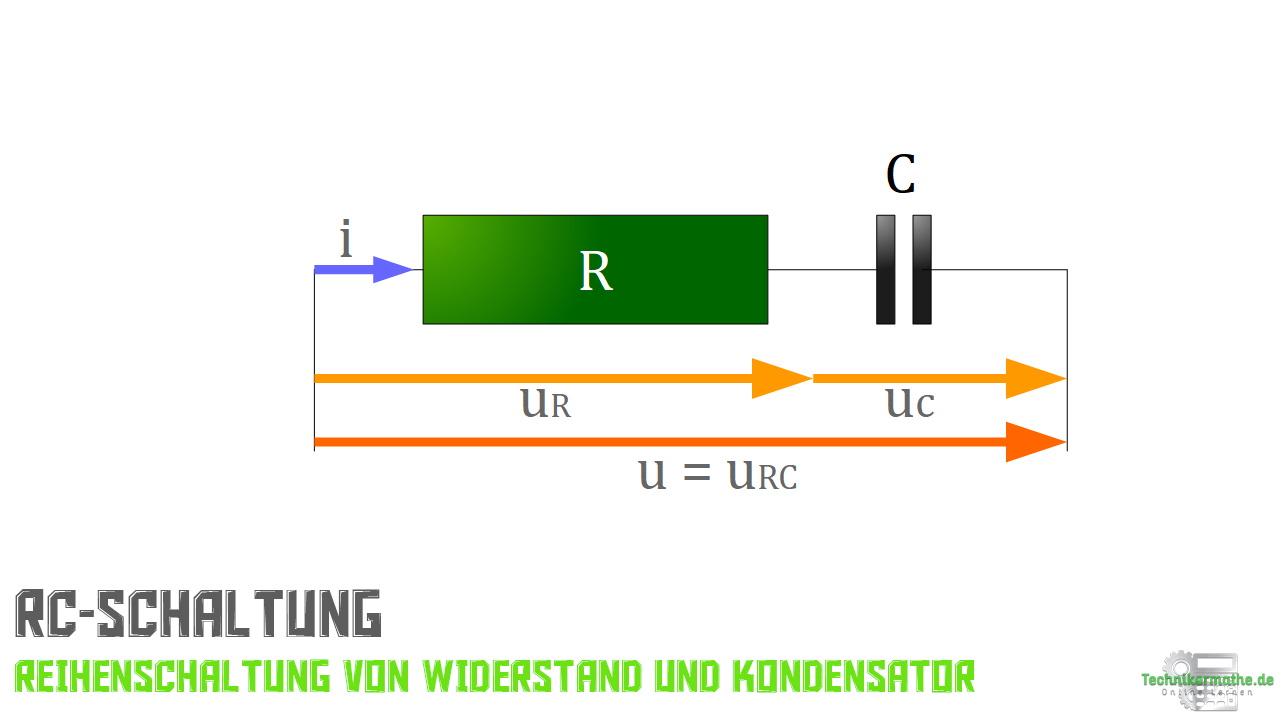
In der zweiten Abbildung siehst du die Spannung und den Strom inklusive Phasenverschiebungswinkel im Zeigerdiagramm dargestellt. Hier betrachten wir das Spannungsdreieck!

Zeigerdiagramm - RC-Schaltung — Zeigerdiagramm – RC-Schaltung

Merk's dir!

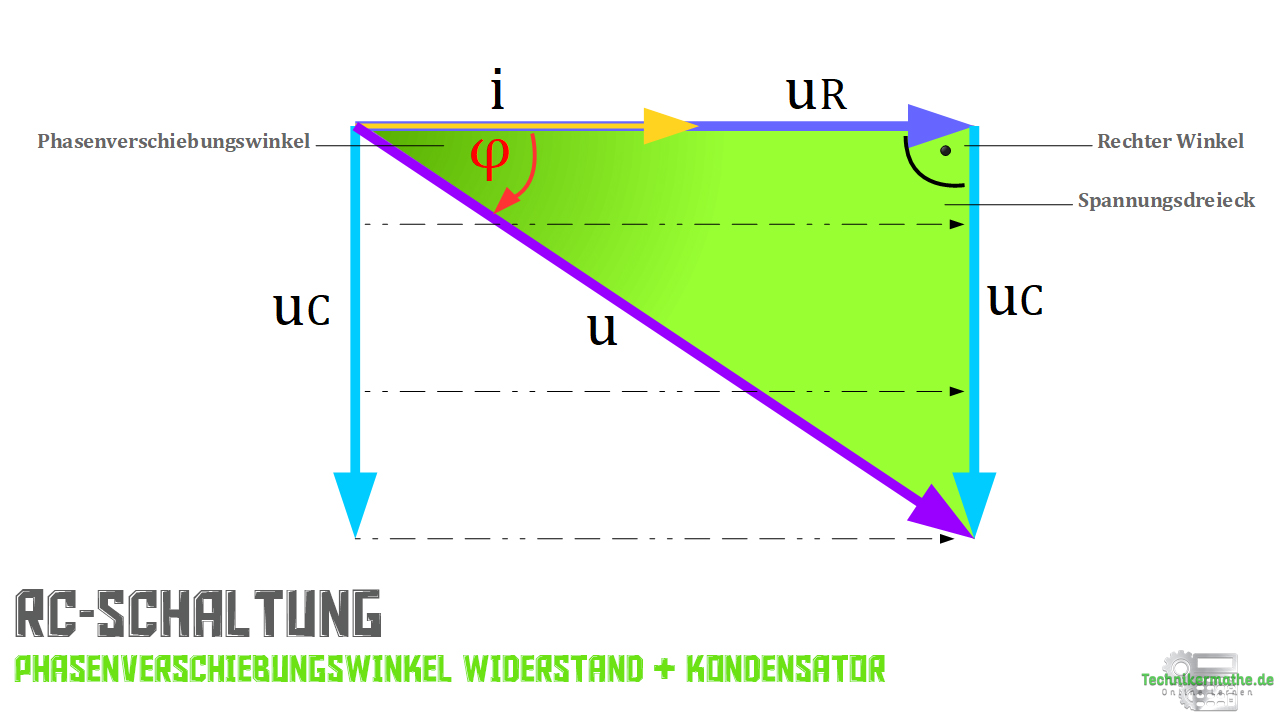
Übrigens die aufgespannte Fläche von $u, u_R$ sowie $u_C$ bezeichnet man als Spannungsdreieck.

In der dritten Abbildung siehst du den Widerstand und die Blindwiderstände inklusive Phasenverschiebungswinkel im Zeigerdiagramm dargestellt. Hier betrachten wir das Widerstandsdreieck!

Das Ohmsche Gesetz gilt generell auch bei Wechselgrößen. Sind die Teilspannungen der einzelnen Widerstände und der Strom bekannt, lässt sich jeder einzelne Widerstandswert errechnen. Da die Spannungen proportional zu den jeweiligen Widerstandswerten sind, können die Teilspannungen im Spannungsdreieck durch die Widerstandswerte ersetzt werden. Anstelle von uR steht dann R und uC wird durch XC ersetzt. Die Gesamtspannung u ist am Gesamtwiderstand, dem Scheinwiderstand oder der Impedanz Z messbar. Das Zeigerdiagramm der Widerstände ist proportional zum Zeigerdiagramm der Spannungen.

Rechnerische Ermittlung

Gleichungen aus dem Spannungsdreieck

$\boxed{ u = \sqrt{u_R^2 + u_C^2} }$

$\boxed{ u = Z \cdot I }$

$\boxed{ u_R = R \cdot i }$

$\boxed{ u_C = X_C \cdot i }$

Gleichungen aus dem Widerstandsdreieck

$\boxed{ Z \cdot i = \sqrt{(R \cdot i)^2 + (X_C \cdot i)^2}}$

$\boxed{ Z = \sqrt{R^2 + X_C^2}}$

Phasenwinkel – RL-Reihenschaltung

Der Phasenwinkel des Stromzeigers beträgt $\varphi = 0 °$

R-Element (Ohmscher Wirkwiderstand): Spannung und Strom liegen in Phase

$\boxed{ \rightarrow \varphi = 0° }$

L-Element ( Induktiver Blindwiderstand [Spule]): Spannung läuft dem Strom mit dem Phasenwinkel

$\boxed{ \rightarrow \varphi = +90° }$

voraus.

Grafische Ermittlung

In der nächsten Abbildung findest du eine typische RL-Reihenschaltung:

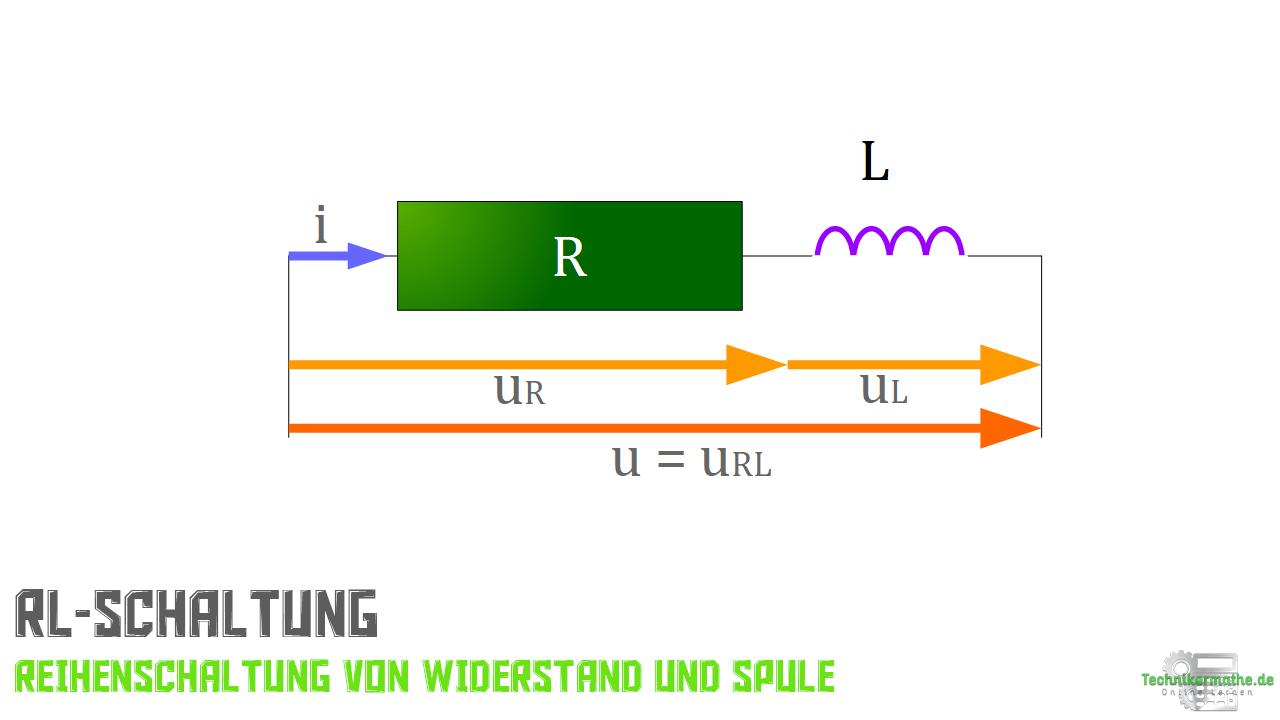
In der zweiten Abbildung siehst du die Spannung und den Strom inklusive Phasenverschiebungswinkel im Zeigerdiagramm dargestellt.

Zeigerdiagramm - RL-Schaltung — Zeigerdiagramm – RL-Schaltung

In der dritten Abbildung siehst du den Widerstand und die Blindwiderstände inklusive Phasenverschiebungswinkel im Zeigerdiagramm dargestellt. Hier betrachten wir das Widerstandsdreieck!

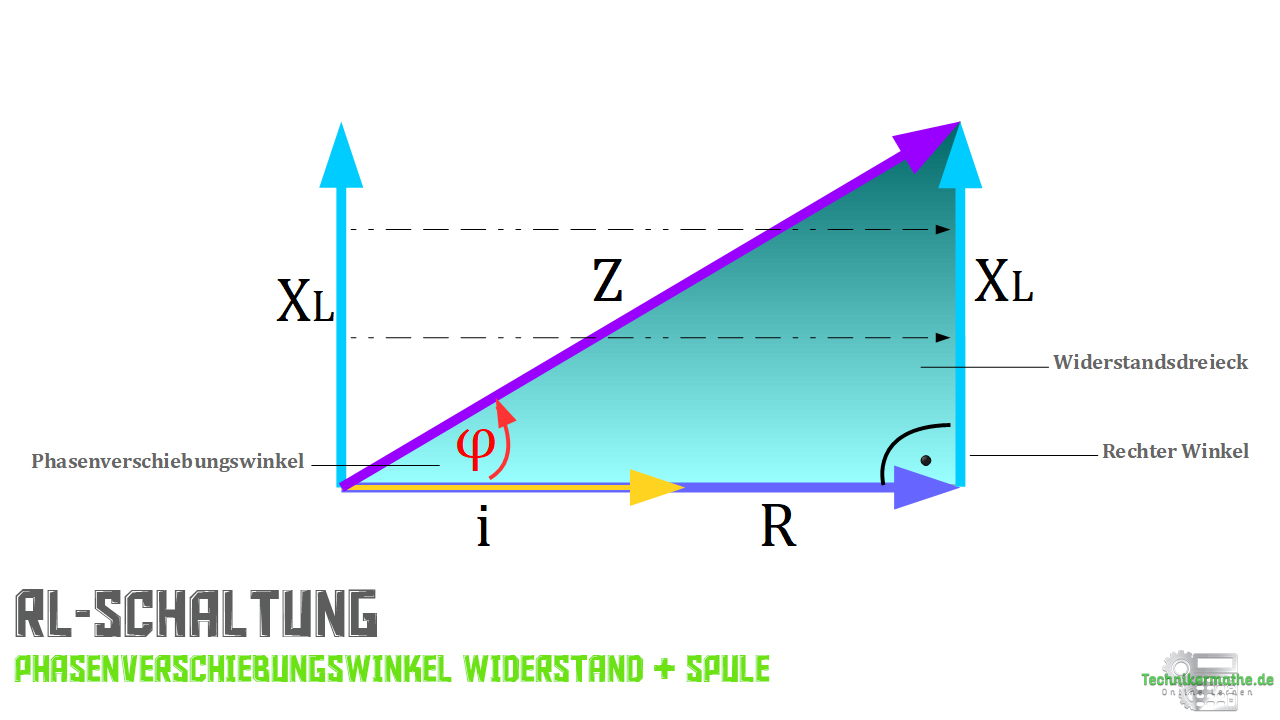
Rechnerische Ermittlung

Gleichungen aus dem Spannungsdreieck

$\boxed{ u = \sqrt{u_R^2 + u_L^2} }$

$\boxed{ tan \varphi = \frac{u_L}{u_R} }$

Gleichungen aus dem Widerstandsdreieck

$\boxed{ Z = \sqrt{(R)^2 + (X_L)^2}}$

$\boxed{ tan \varphi = \frac{X_L}{R}}$

Phasenwinkel – RCL-Reihenschaltung

Das Zeigerdiagramm ist eine Kombination der beiden zuvor beschriebenen Reihenschaltungen.

Der Phasenwinkel des Stromzeigers beträgt $\varphi = 0 °$

R-Element (Ohmscher Wirkwiderstand): Spannung und Strom liegen in Phase

$\boxed{ \rightarrow \varphi = 0° }$

C-Element ( Kapazitiver Blindwiderstand [Kondensator]): Spannung läuft dem Strom mit dem Phasenwinkel

$\boxed{ \rightarrow \varphi = -90° }$

nach.

L-Element ( Induktiver Blindwiderstand [Spule]): Spannung läuft dem Strom mit dem Phasenwinkel

$\boxed{ \rightarrow \varphi = +90° }$

voraus.

Grafische Ermittlung

In der nächsten Abbildung findest du eine typische RLC-Reihenschaltung:

Phasenverschiebungswinkel, RLC-Schaltung

In der zweiten Abbildung siehst du die Spannung und den Strom inklusive Phasenverschiebungswinkel im Zeigerdiagramm dargestellt. Hier ist $X_L$ wesentlich größer als $X_C$

Zeigerdiagramm - RLC-Schaltung — Zeigerdiagramm – RLC-Schaltung

In der zweiten Abbildung siehst du die Spannung und den Strom inklusive Phasenverschiebungswinkel im Zeigerdiagramm dargestellt.

In Abhängigkeit von den Zeigerlängen nimmt der Phasenwinkel zwischen Strom und Spannung positive oder negative Werte an. Die RCL-Reihenschaltung wirkt nach außen hin mit +φ mehr induktiv und mit −φ mehr kapazitiv.

“Die Zeiger beider Blindkomponenten weisen mit 180° in entgegengesetzte Richtungen.”

Für eine charakteristische Frequenz sind sie gleich lang und ihre Beträge heben sich rechnerisch auf. Mit dem verbleibenden ohmschen Wirkanteil verhält sich die Schaltung dann insgesamt wie ein ohmscher Widerstand, bei dem Strom und Spannung in Phase sind.

Rechnerische Ermittlung

Gleichung für den Fall, dass $X_L > X_C$ ist:

Aus dem Spannungdreieck:

$\boxed{ u = \frac{u_R^2 + (u_L - u_C)^2} }$

$\boxed{ tan \varphi = \frac{u_L - u_C}{u_R} }$

Aus dem Widerstandsdreieck:

$\boxed{ Z = \frac{R^2 + (X_L - X_C)^2}}$

$\boxed{ tan \varphi = \frac{X_L - X_C}{R} }$

Gleichung für den Fall, dass $X_L < X_C$ ist:

Aus dem Spannungdreieck:

$\boxed{ u = \frac{u_R^2 + (u_C - u_L)^2} }$

$\boxed{ tan \varphi = \frac{u_C - u_L}{u_R} }$

Aus dem Widerstandsdreieck:

$\boxed{ Z = \frac{R^2 + (X_C - X_L)^2} }$

$\boxed{ tan \varphi = \frac{X_C - X_L}{R} }$

Phasenwinkel – RC-Parallelschaltung

Widerstände liegen in einer Parallelschaltung alle an derselben Spannung, die im Zeigerdiagramm zur Bezugsgröße wird. Der Spannungszeiger weist in x-Achsenrichtung mit dem Winkel φ = 0°.

Am Wirkwiderstand weist der Stromzeiger in die gleiche Richtung, da der Phasenwinkel 0° beträgt.

Am kapazitiven Blindwiderstand eilt der Strom um +90° voraus und der Stromzeiger zeigt in die positive y-Achsenrichtung.

Grafische Ermittlung

In der nächsten Abbildung findest du eine typische RC-Parallelschaltung:

In der zweiten Abbildung siehst du die Spannung und den Strom inklusive Phasenverschiebungswinkel im Zeigerdiagramm dargestellt. Hier betrachten wir das Stromdreieck!

Zeigerdiagramm - RC-Diagramm — Zeigerdiagramm – RC-Diagramm

In der dritten Abbildung siehst du den Leitwert und die Blindleitwert inklusive Phasenverschiebungswinkel im Zeigerdiagramm dargestellt. Hier betrachten wir das Leitwertdreieck!

Es kann ein rechtwinkliges Stromdreieck gezeichnet werden. Der Gesamtstrom errechnet aus der geometrischen Addition der Teilströme. Der Phasenwinkel zwischen Spannung und Strom ergibt sich aus tanφ, dem Quotienten von Blindkomponente zur Wirkkomponente.

Die Teilströme sind direkt proportional zu den Leitwerten.

Das Stromdreieck kann folglich in ein verhältnisgleiches Leitwertdreieck umgezeichnet werden. Die Leitwerte lassen sich durch die Kehrwerte der entsprechenden Widerstandswerte ersetzen.

Rechnerische Ermittlung

Aus dem Stromdreieck

$\boxed{ i = \sqrt{i_R^2 + i_C^2}}$

$\boxed{ tan \varphi = \frac{i_C}{i_R} }$

Aus dem Leitwertdreieck

$\boxed{ Y = \sqrt{G^2 + B_C^2} }$

$\boxed{ tan \varphi = \frac{B_C}{G}}$

Rechnen mit den Widerstandswerten

Übertragen auf die Widerstandswerte gilt mit $Y = \frac{1}{Z}$ , $G = \frac{1}{R}$ , $B_C = \frac{1}{X_C}$ :

$\boxed{Z = \frac{R \cdot X_C}{\sqrt{R^2 + X_C^2}} }$

$\boxed{tan \varphi = \frac{R}{X_C }}$

Phasenwinkel – RL-Parallelschaltung

Die an der Parallelschaltung anliegende Wechselspannung ist die Bezugsgröße.

Am Wirkwiderstand sind Spannung und Strom mit φ = 0° in Phase.

Am induktiven Blindwiderstand der Spule eilt der Strom um φ = −90° der Spannung nach.

Grafische Ermittlung

In der nächsten Abbildung findest du eine typische RL-Parallelschaltung:

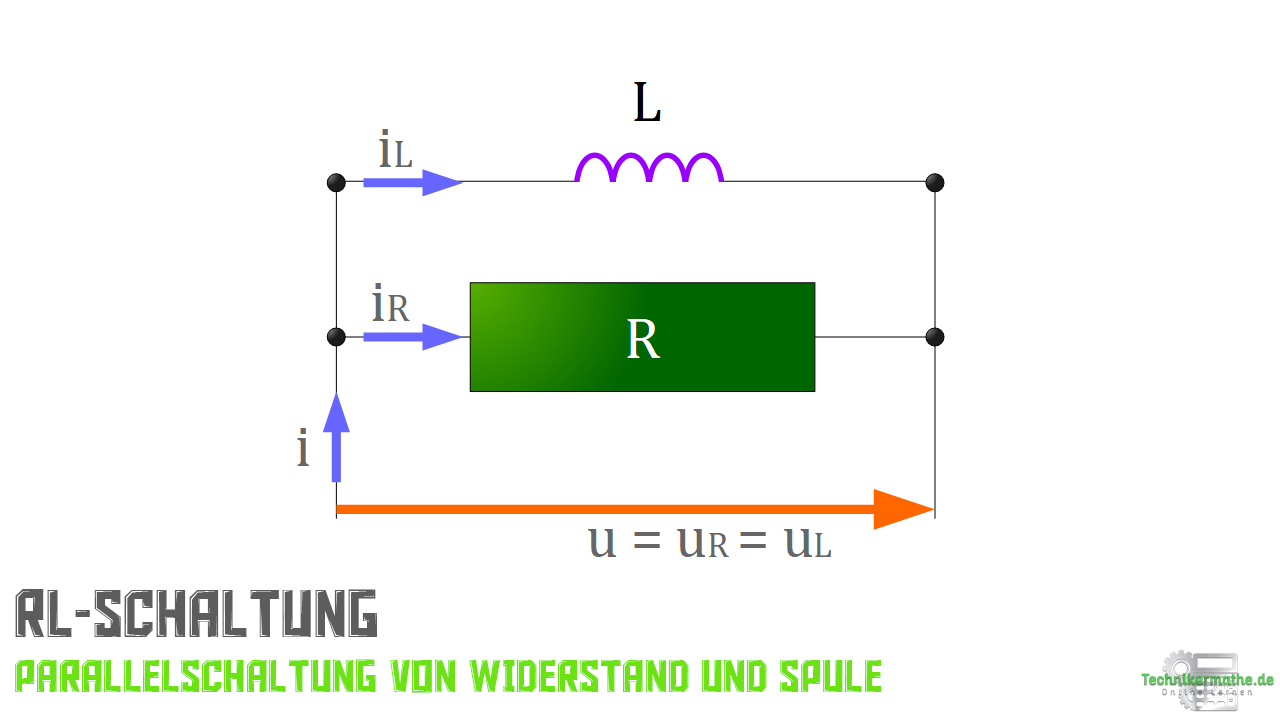
In der zweiten Abbildung siehst du die Spannung und den Strom inklusive Phasenverschiebungswinkel im Zeigerdiagramm dargestellt. Hier betrachten wir das Stromdreieck!

In der dritten Abbildung siehst du den Leitwert und die Blindleitwert inklusive Phasenverschiebungswinkel im Zeigerdiagramm dargestellt. Hier betrachten wir das Leitwertdreieck!

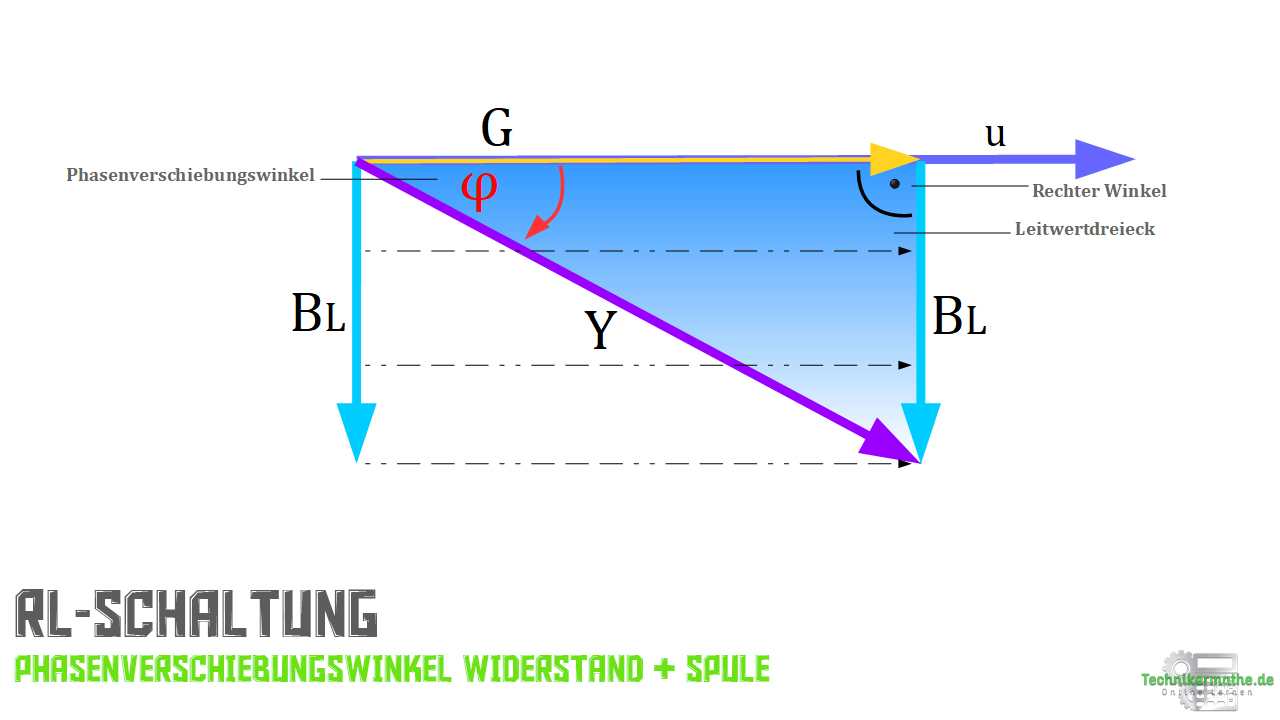
Rechnerische Ermittlung

Aus dem Stromdreieck

$\boxed{ i = \sqrt{i_R^2 + i_L^2}}$

$\boxed{ tan \varphi = \frac{i_L}{i_R} }$

Aus dem Leitwertdreieck

$\boxed{ Y = \sqrt{G^2 + B_L^2} }$

$\boxed{ tan \varphi = \frac{B_L}{G}}$

Rechnen mit den Widerstandswerten

Übertragen auf die Widerstandswerte gilt mit $Y = \frac{1}{Z}$ , $G = \frac{1}{R}$ , $B_L = \frac{1}{X_L}}$ :

$\boxed{Z = \frac{R \cdot X_L}{\sqrt{R^2 + X_L^2}}}$

$\boxed{tan \varphi = \frac{R}{X_L}}$

Phasenwinkel – RCL-Parallelschaltung

Die Bezugsgröße mit φ = 0° ist die Wechselspannung.

Spannung und Strom am ohmschen Wirkwiderstand sind phasengleich.

Am kapazitiven Blindwiderstand eilt der Strom um φ = +90° vor und am induktiven Blindwiderstand um φ = −90° nach.

Durch entsprechende Parallelverschiebung der Zeiger kann das Stromdreieck und daraus abgeleitet das Leitwertdreieck gezeichnet werden.

Grafische Ermittlung

In der nächsten Abbildung findest du eine typische RLC-Parallelschaltung:

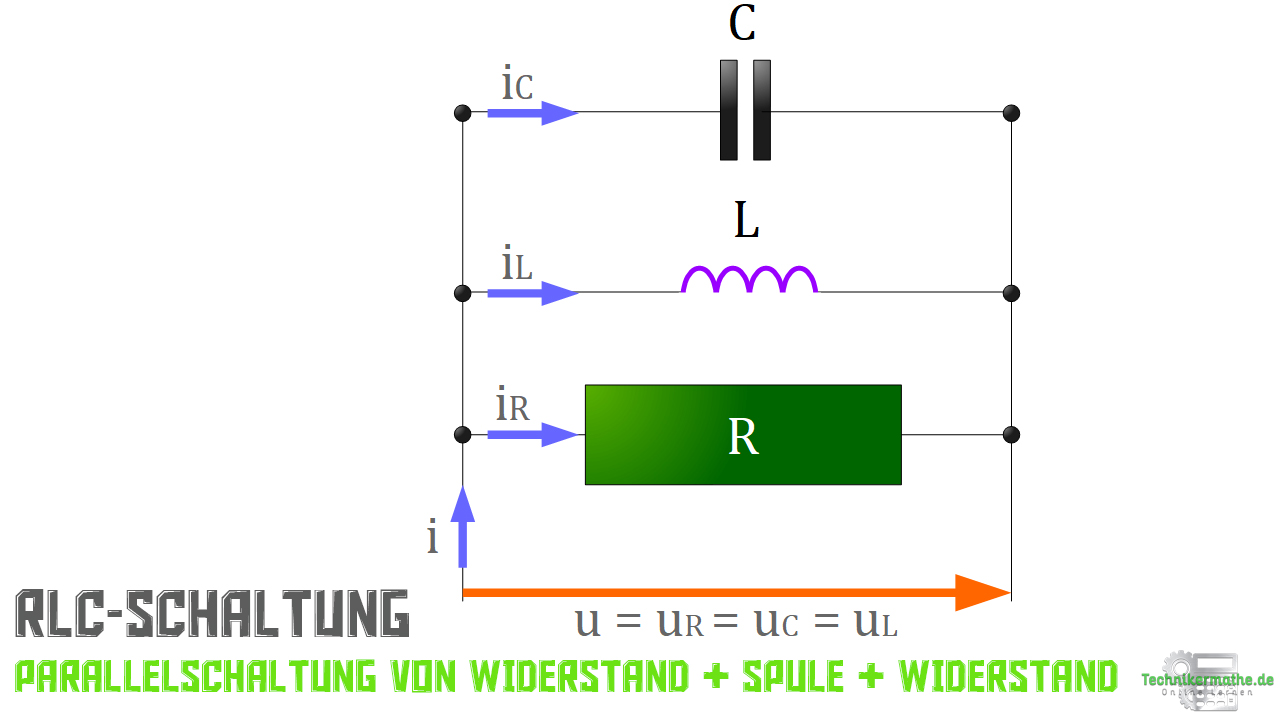
In der zweiten Abbildung siehst du die Wirkleitwerte und die Blindleitwerte inklusive Phasenverschiebungswinkel im Zeigerdiagramm dargestellt.

Der Phasenwinkel kann positive oder negative Werte annehmen, je nachdem ob die Induktivität oder die Kapazität mit ihren Werten den Schaltungscharakter bestimmt. Sind beide Blindkomponenten gleich groß, so wirkt die RCL-Parallelschaltung nach außen hin wie ein ohmscher Widerstand mit φ = 0°.

Rechnerische Ermittlung

Gleichung für den Fall, dass $B_C > B_L$ ist:

Aus dem Stromdreieck:

$\boxed{ u =\sqrt{u_R^2 + (u_C - u_L)^2} }$

$\boxed{ tan \varphi = \frac{u_C - u_L}{u_R} }$

Aus dem Leitwertdreieck:

$\boxed{ Y = \sqrt{G^2 + (B_C - B_L)^2}}$

$\boxed{ tan \varphi = \frac{B_C - B_L}{G} }$

Gleichung für den Fall, dass $B_C < B_L$ ist:

Aus dem Stromdreieck:

$\boxed{ u = \sqrt{u_R^2 + (u_L - u_C)^2} }$

$\boxed{ tan \varphi = \frac{u_L - u_C}{u_R} }$

Aus dem Leitwertdreieck:

$\boxed{Y = \sqrt{R^2 + (B_L - X_C)^2} }$

$\boxed{ tan \varphi = \frac{B_L -B_C}{G} }$

wie gehts weiter?

Nachdem du jetzt den Phasenverschiebungswinkel kennengelernt hast, möchten wir dir im nächsten Kurstext noch mal die beiden Größen Leistung und Arbeit im Zusammenhang mit der Wechselstromtechnik vorstellen.

Was gibt es noch bei uns?

Finde die richtige Schule für dich!

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe.de?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Interaktive Übungsaufgaben

Trainingsbereich

Quizfrage 1

Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?

Auszüge aus unserem Kursangebot

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
ET6 (Wechselstromtechnik 1) und
TM1 (Technische Mechanik – Statik) an.

Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++