(ET5-043) – Blindwiderstand und Leitwert [Grundlagen, Formeln, Lernclip, Beispiele]

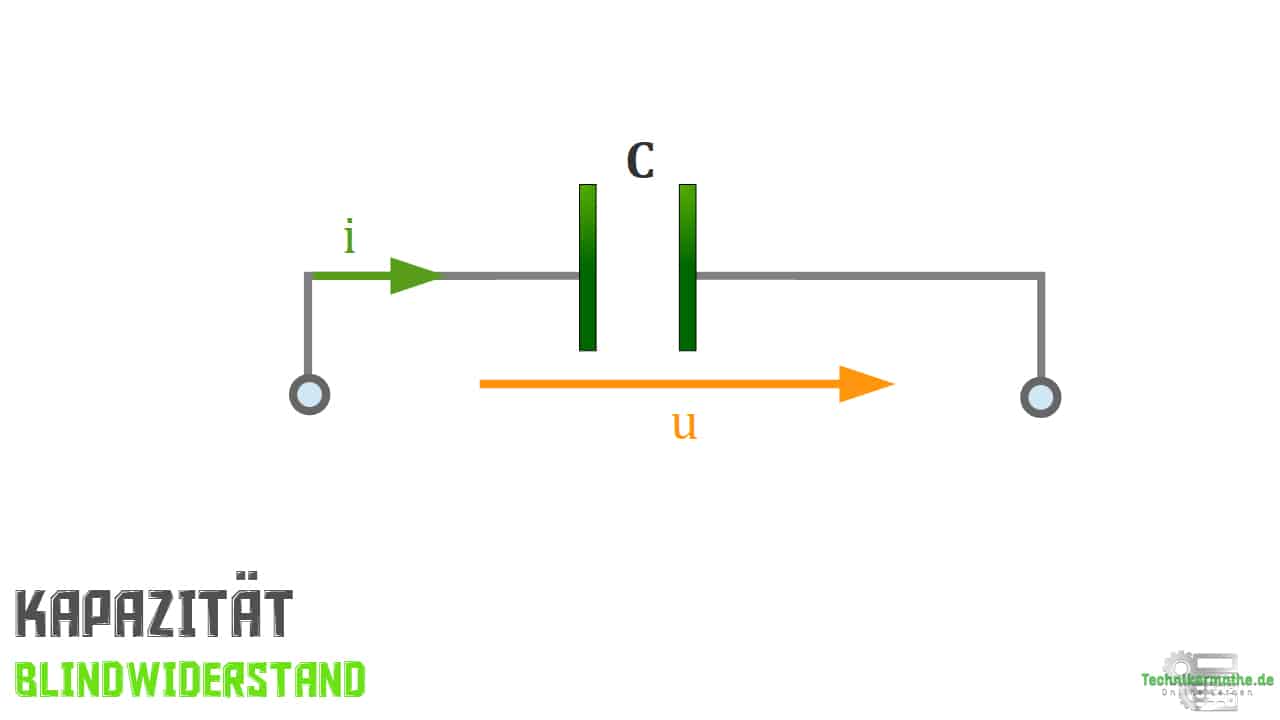
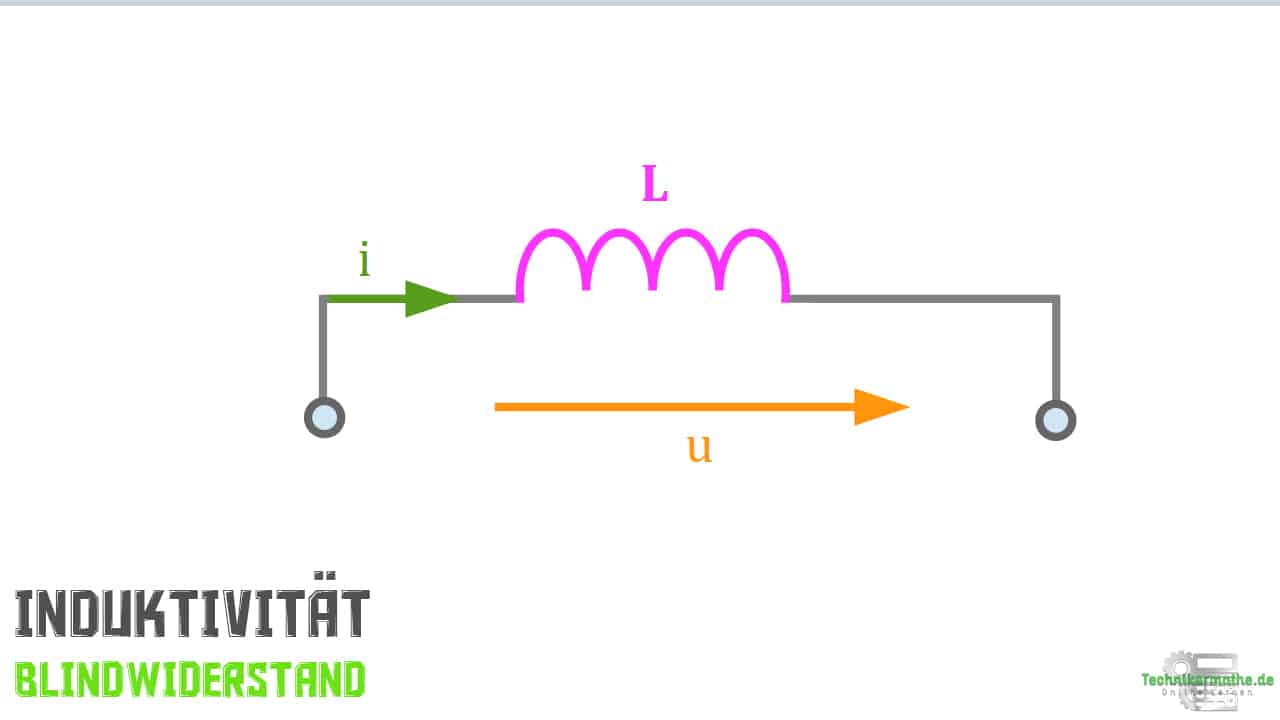
In diesem Kurstext stellen wir dir den Blindwiderstand für L C vor, also eine Induktivität und Kapazität sowie den Leitwert im Zusammenhang mit R L C, also mit einem Widerstand, einer Induktivität , einer Kapazität vor. Mit Hilfe dieser Angaben kannst du Berechnungen durchführen und einen Vergleich zwischen diesen drei Größen ziehen.

Außerdem erfährst du was hinter Begriffen wie [Induktanz] steckt.

Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET6-Wechselstromtechnik 1

Die Vertiefung der Wechselstromtechnik findest du im Kurs: ET7-Wechselstromtechnik 2

Merk’s dir!

“Es besteht grundsätzlich immer ein Unterschied zwischen Wirkwiderständen (R) und Blindwiderständen (L, C).”

Blindwiderstand – Grundlagen

Wie sich das äußert, erfährst du nachfolgend.

Blindwiderstand, Leitwert - Spulen und Kondensatoren — Blindwiderstand, Leitwert – Spulen und Kondensatoren

Der Blindwiderstand ist eine Größe aus der Elektrotechnik, die uns erlaubt einen Wechselstrom $i$ durch den Aufbau einer Wechselspannung $u$ zu begrenzen. Dabei kommt es zu einer zeitlichen Phasenverschiebung zwischen den beiden Größen Spannung und Stromstärke.

“In der Fachliteratur findest du nicht selten den alternativen Begriff Reaktanz.”

Kann der wirklich nichts sehen?…

Nein, das ist natürlich Quatsch. Der Begriff “Blind..” rührt daher, dass die elektrische Energie zwar zu den besagten Widerständen befördert wird, dort aber, anders als beispielsweise bei Ohm’schen Verbrauchern, keine thermische, chemische oder mechanische Energieumwandlung bewirkt. Bei Ohm’schen Verbrauchern kann man diese Umwandlungseffekte häufig beobachten.

Wie hoch der Wert des Blindwiderstands ausfällt richtet sich nach der Frequenz.

Induktiver und kapazitiver Blindwiderstand

Merk’s dir!

Spulen und Kondensatoren haben gemein, dass sie Energiespeicher sind.

Jedoch speichern beide Bauteile auf unterschiedliche Art und Weise.

Hey Spule, hey Kondensator, wer von euch macht was?…

Die beiden elektrischen Bauteile unterscheiden sich dahingehend, dass

der Kondensator durch einen Stromfluss ein elektrisches Feld aufbaut

Blindwiderstand, Kapazität – Darstellung im Schaltkreis (als Schaltzeichen)

und

die Spule durch eine angelegte Spannung ein Magnetfeld aufbaut.

Blindwiderstand, Spule – Darstellung im Schaltkreis (als Schaltzeichen)

Je nach dem ob wir von einer Spule (Induktivität) oder einem Kondensator (Kapazität) sprechen, liegt uns entweder ein induktiver oder im zweiten Fall ein kapazitiver Blindwiderstand vor.

Dieser Speichervorgang führt dazu, dass der Stromquelle oder Spannungsquelle permanent elektrische Energie entzogen wird.

Ändern wir jedoch die Strom- oder Spannungsrichtung wird diese elektrische Energie wieder den Quellen zugeführt.

Dies ist bei einem Wirkwiderstand nicht möglich. Da wir meistens von einem Sinusförmigen Verlauf der Wechselgrößen ausgehen, erfolgt das Auf- und Entladen der Energiespeicher periodisch.

Blindstrom, Blindwiderstand, Blindenergie

Blindstrom: Die Verursacher dieses Vorgangs sind der sinusförmige Spannungsverlauf und der phasenverschobene sinusförmige Stromverlauf. Letzteren nennt man übrigens Blindstrom.
Blindwiderstand: Das Verhältnis zwischen der Spannung und der um eine viertel Periodendauer 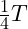$\frac{1}{4}T$ verschobene Stromstärke bezeichnet man als Blindwiderstand.
Blindenergie: Die zwischen der Quelle und dem Energiespeicher pendelnde Energie bezeichnet man als Blindenergie.

Ohmsch-induktiver und Ohmsch-kapazitiver Verbraucher am Stromnetz

Ein linearer Blindwiderstand (ideal) erzeugt ja nur eine Blindleistung im Netz, eine Wirkleistung verbraucht er hingegen nicht. Denn die für den Auf- und Abbau der elektrischen und magnetischen Felder benötigte Energie wird ja an den Erzeuger (Quellen) zurückgegeben.

Eigentlich ja kein Problem, aber dies führt jedoch zu einer erhöhten Belastung der Leitungen.

In der Realität treten Blindwiderstände immer mit Wirkwiderständen zusammen auf, da es ja bekanntlich keine verlustlosen Stromkreise gibt und daher tatsächlich Leistung umgesetzt werden muss.

Überwiegt in einem Verbraucher der induktive Blindwiderstand gegenüber dem kapazitiven, so wird der Verbraucher als ohmsch-induktiv bezeichnet

Beispiel: ohmsch-induktive Verbraucher!

Elektromotoren
Transformatoren
Leuchtstofflampen

Überwiegt in einem Verbraucher der kapazitive Blindwiderstand gegenüber dem induktiven, so wird der Verbraucher als ohmsch-kapazitiv bezeichnet.

Beispiel: ohmsch-kapazitive Verbraucher!

Computernetzteile
Kondensatornetzteile
Frequenzumrichter

Blindwiderstand – Berechnung

Wir gehen bei dieser aber auch bei den nachfolgenden Berechnungen in späteren Kurstexten der Einfachheit halber immer von sinusförmigen Verläufen von Wechselstrom und Wechselspannung aus.

Merk’s dir!

Das Kurzzeichen für den Blindwiderstand ist X und die Einheit ist Ohm Ω .

Impedanz – Imaginärteil und Realteil

Aus mathematischer Sicht ist der Blindwiderstand in der Elektrotechnik bei einer Wechselstromrechnung der Imaginärteil des komplexen Widerstandes $\underline{Z}$

“In der Fachliteratur findest du nicht selten für $\underline{Z}$ den alternativen Begriff Impedanz.”

Wo ein Imaginärteil existiert sollte auch ein Realteil von $\underline{Z}$ existieren.

Diesen “realen” Teil der Impedanz bezeichnen wir als Wirkwiderstand $R$ .

Wie das Aussieht zeigt dir das nachfolgende Bild. Die Impedanz ist als Widerstandszeiger dargestellt.

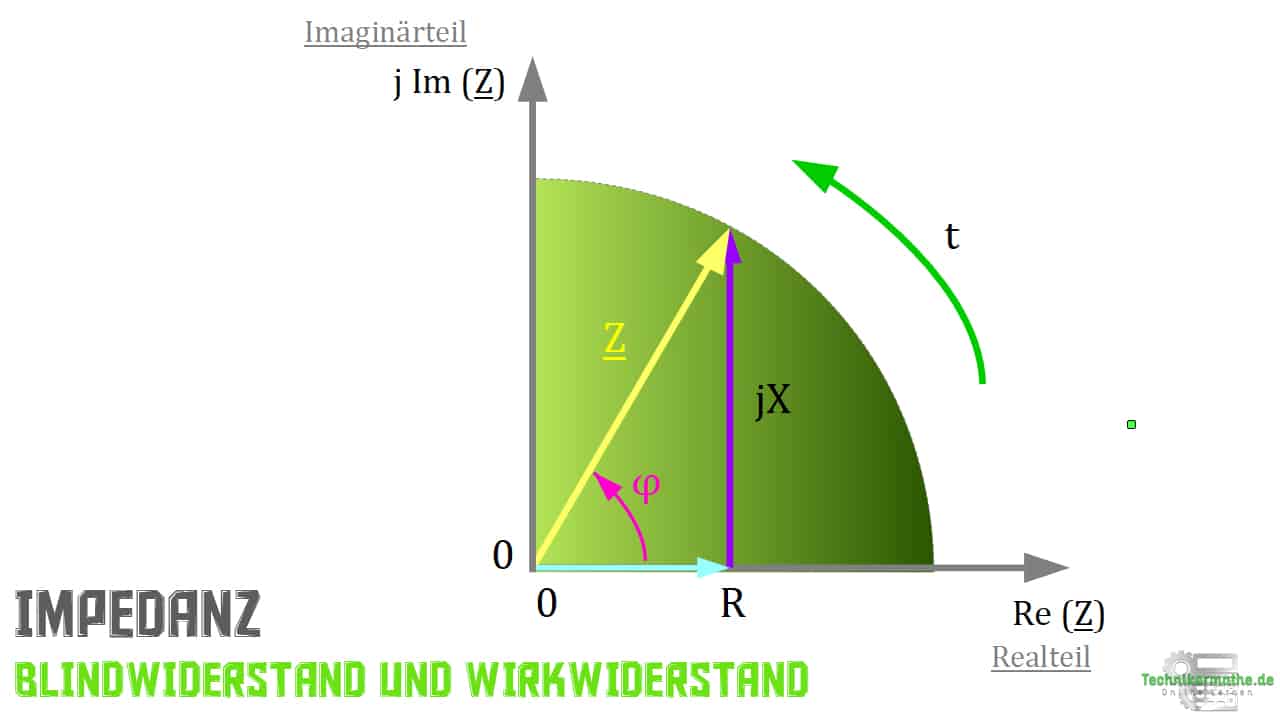
Blindwiderstand und Wirkwiderstand im Koordinatensystem

Hier ergibt sich mit Hilfe der grafischen Vektoraddition (folgt später im Kurs ausführlich) von Wirkwiderstand $R$ und Blindwiderstand $X$ ein Widerstandszeiger $\underline{Z}$ . Alternativ kannst du auch den Satz des Pythagoras verwenden, da es sich um ein Rechtwinkliges Dreieck handelt.

Für die Impedanz gilt allgemein:

$\underline{Z} = \frac{\underline{u}}{\underline{i}} = R + j \cdot X$ Impedanz

$j$ ist die imaginäre Einheit.

Für den Betrag der Impedanz gilt:

$|\underline{Z}| = Z = \sqrt{R^2 + X^2}$ Betrag der Impedanz

Blindwiderstand – Allgemeine Formel

Aber kommen wir nun zu der mathematischen Herleitung:

$X = Im \underline{Z} = Im \frac{\underline{u}}{\underline{i}}$

daraus folgt

$X = Z \cdot sin \varphi = \frac{U}{I} \cdot sin \varphi$

Daraus können wir ableiten für die allgemeine Form des Blindwiderstandes, dass des pro Periodendauer zwei Geltungsbereiche gibt:

$X = \sqrt{ Z^2 - R^2} }$ – bei $0 \le \varphi \le 90°$

$X = - \sqrt{ Z^2 - R^2} }$ – bei $- 90° \le \varphi \le 0$

Wir bestimmen die Blindwiderstände für die Spule und den Kondensator. Dabei gehen wir ausgehend vom vorherigen Kurstext wie folgt vor.

Zuerst überführen wir die Gleichung für die Ströme von Spule $i_L$ und Kondensator $i_C$ in die allgemeine Gleichung von $i$ :

Hier gilt:

$i = \sqrt{2 } I sin (\omega t - \frac{\pi}{2})$

Nehmen wir jetzt das Ohmsche Gesetz zur Hand, so können wir neben der allgemeinen Gleichung für einen Ohmschen Widerstand, auch die Gleichungen für die Effektivströme von Spule und Kondensator aufstellen.

$I_R = \frac{U}{R}$ Effektivstrom des Widerstandes

$I_L = \frac{U}{X_L}$ Effektivstrom der Spule

$I_C = \frac{U}{X_C}$ Effektivstrom des Kondensators

In der zweiten und dritten Gleichung finden wir im Nenner nicht die Angabe des Widerstandswertes, sondern jeweils lediglich die Angabe des Blindwiderstandes für die Spule und den Kondensator.

Diese sind uns bis Dato aber noch unbekannt.

Abhilfe schaffen die beiden Gleichungen für $i_L$ und $i_C$ aus dem vorherigen Kurstext:

$i_L = - \sqrt{2} \cdot \frac{U}{\omega \cdot L} \cdot sin(\omega t - \frac{\pi}{2})$

$i_C = \sqrt{2} U \cdot \omega \cdot C \cdot sin(\omega t - \frac{\pi}{2})$

Mit diesen können wir jetzt die beiden Gleichungen für den Blindwiderstand aufstellen:

Blindwiderstand – Spule (= Induktanz) – Formel

Für die Berechnung ziehen wir die Gleichung für die Impedanz einer idealen Spule heran

$\underline{Z}_L = j \cdot \omega \cdot L = j \cdot X_L$ Impedanz der Spule

$j$ ist die imaginäre Einheit.

Der Induktanz (Widerstandswert) für die Spule lässt sich mit der nachfolgenden Gleichung errechnen:

$X_L = \omega \cdot L$ Induktanz

Ausgeschrieben erhalten wir:

$X_L = 2 \cdot \pi \cdot f \cdot L$ Induktanz

Blindwiderstand – Kondensator (= Kapazitanz) – Formel

Für die Berechnung ziehen wir die Gleichung für die Impedanz eines idealen Kondensators heran

$\underline{Z}_C = \frac{1}{ j \cdot \omega \cdot C} = \frac{- j}{w \cdot C} = j \cdot X_C$ Impedanz der Spule

$j$ ist die imaginäre Einheit.

Der Kapazitanz (Widerstandswert) für den Kondensator lässt sich mit der nachfolgenden Gleichung errechnen:

$X_C = - \frac{1}{\omega \cdot C}$ Kapazitanz

Ausgeschrieben erhalten wir:

$X_C = - \frac{1}{2 \cdot \pi \cdot f \cdot C}$ Kapazitanz

“Der Kondensatorstrom hat eine gegenläufige Phasenlage im Gegensatz zum Strom der Spule”

Leitwert – Grundlagen

Der elektrische Leitwert ist der Kehrwert eines Widerstandes. Damit ist dieser auch eine Kenngröße für ein elektrisches Bauteil.

Merk’s dir!

Fälschlicherweise verwechseln viele den Leitwert mit der Leitfähigkeit! Du aber nicht, denn du weißt, dass es sich bei der Leitfähigkeit um eine Materialkonstante handelt.

Leitwert Berechnung

Manchmal erfordert eine Berechnung nicht die Angabe eines Widerstandswertes sondern die eines Leitwertes. Die

Merk’s dir!

Das Kurzzeichen für den elektrischen Leitwert ist G oder B und die Einheit ist Siemens [S]

Um den Leitwert für die drei elektrischen Bauteile zu errechnen, gehen wir nach dem bekannten Muster aus dem Grundlagenkurs ET1 vor. Hier ergibt sich der Leitwert immer aus dem Kehrwert des Widerstandswertes.

Somit kann der elektrische Leitwert immer aus dem Widerstand bzw. den Werten von Stromstärke $i$ und Spannung $u$ errechnet werden.

Leitwert – Widerstand – Formel

Die Gleichung zur Berechnung des Leitwertes für einen Widerstand ist folgende:

$G = \frac{1}{R}$ Leitwert – Widerstand

Leitwert – Spule – Formel

Die Gleichung für die Berechnung des Leitwertes einer Spule ist folgende:

$B_L = \frac{1}{X_L}$ Leitwert – Spule

Dies entspricht unter Hinzunahme der obigen Gleichung für den Widerstand folgende Formel:

$B_L = \frac{1}{\omega \cdot L}$ Leiterwert – Spule (angepasst)

Leitwert – Kondensator – Formel

Die Gleichung für die Berechnung des Leitwertes einer Kapazität (Spule) ist folgende:

$B_L = \frac{1}{X_C}$ Leitwert – Kondensator

Dies entspricht unter Hinzunahme der obigen Gleichung für den Widerstand folgende Formel:

$B_L = - \omega \cdot C$ Leiterwert – Kondensator (angepasst)

+++ Videoclip – Widerstand & Leitwert – Zusammenfassender Überblick +++

Was kommt als Nächstes?

Nachdem du jetzt den Blindwiderstand und den Leitwert für die drei elektrischen Bauteile kennengelernt hast, stellen wir dir im kommenden Kurstext die Zeigerdiagramme vor.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++