(ET5-042) – R L C im Wechselstrom [Widerstand, Induktivität, Kapazität]

In diesem Kurstext stellen wir dir R L C im Wechselstrom vor und somit die Belastungsarten im Wechselstromkreis durch Widerstand (Ohm’scher Verbraucher) R , Induktivität (Spule) L und Kapazität (Kondensator) C vor.

Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET6-Wechselstromtechnik 1

Die Vertiefung der Wechselstromtechnik findest du im Kurs: ET7-Wechselstromtechnik 2

Merk’s dir!

In der Wechselstromtechnik steht RLC für die drei grundlegenden Komponenten eines elektrischen Schaltkreises: Widerstand (R), Induktivität (L) und Kapazität (C). Diese werden häufig in Wechselstromschaltkreisen gefunden und spielen eine wichtige Rolle bei der Analyse und dem Design von elektrischen Systemen.

Der Widerstand (R) begrenzt den Stromfluss, die Induktivität (L) erzeugt eine Phasenverschiebung zwischen Strom und Spannung, und die Kapazität (C) speichert elektrische Ladung.

Die Kombination dieser drei Elemente in einem Schaltkreis kann komplexe Verhaltensweisen wie Resonanz, Impedanz und Phasenverschiebung hervorrufen, die für die Wechselstromtechnik von entscheidender Bedeutung sind.

R L C im Wechselstrom – Überblick

Für die drei benannten Größen (elektrische Bauteile) möchten wir dir nun nacheinander vorstellen und dazu die notwendigen Formeln (Sinusströme und Sinusspannungen) aufstellen, die wir für spätere Berechnungen benötigen.

Als Grundlage dienen uns die allgemeinen Gleichungen für die Berechnungen von R L C im Wechselstrom

$R =$ Widerstand (Ohm’scher Verbraucher)

$L =$ Induktivität (Spule)

$C =$ Kapazität (Kondensator)

R L C im Wechselstrom – Schaltzeichen und Allgemeine Spannungsgleichung für R, L, C

Wir schauen uns nun die einzelnen Bauteile nacheinander an.

R | (Ohm’scher Verbraucher – Widerstand)

Nachfolgend siehst du das typische Schaltzeichen für einen elektrischen Widerstand:

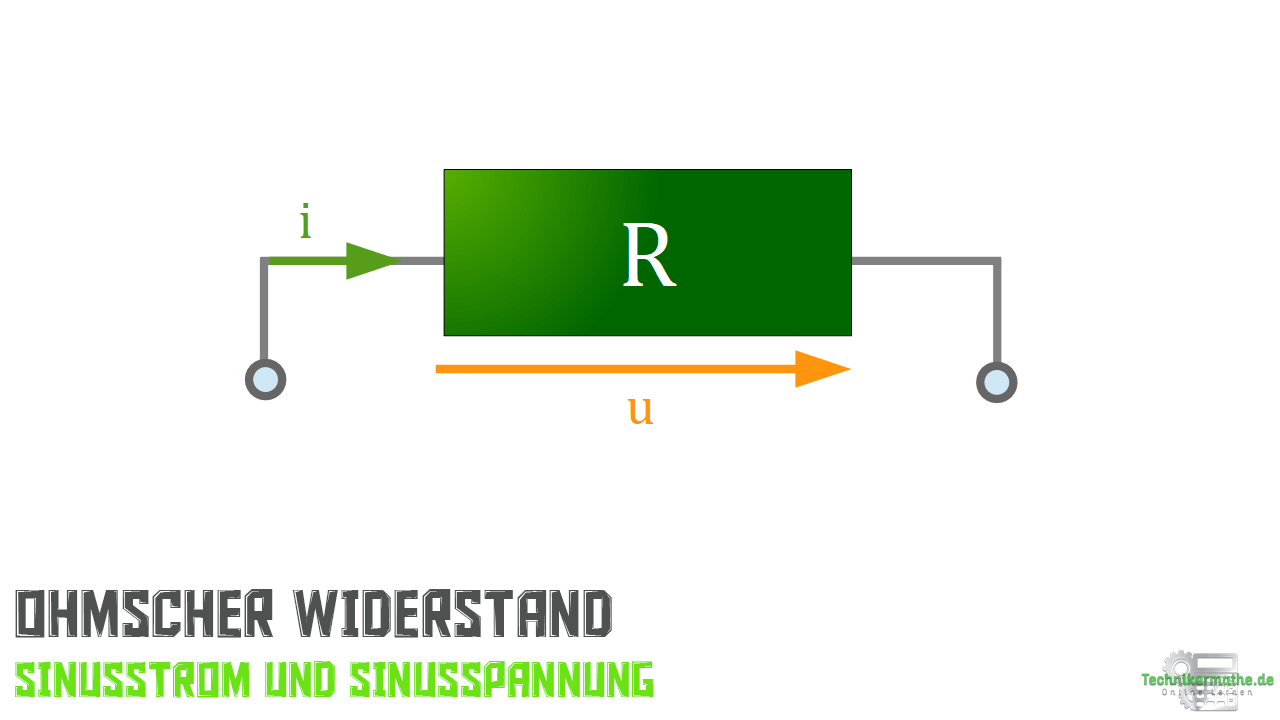
R-L-C-im-Wechselstrom - Schaltzeichen: Ohm'scher Widerstand im Schaltkreis — R-L-C-im-Wechselstrom – Schaltzeichen: Ohm’scher Widerstand im Schaltkreis

Die zugehörige Gleichung für die Berechnung der Spannung eines elektrischen Widerstandes in einem Wechselstromkreis ist:

$u = i \cdot R$

Merk’s dir!

Hierbei handelt es sich um eine für die Wechselstromtechnik angepasste Version des Ohm’schen Gesetzes.

L | (Spule – Induktivität)

Nachfolgend siehst du das typische Schaltzeichen für eine elektrische Spule:

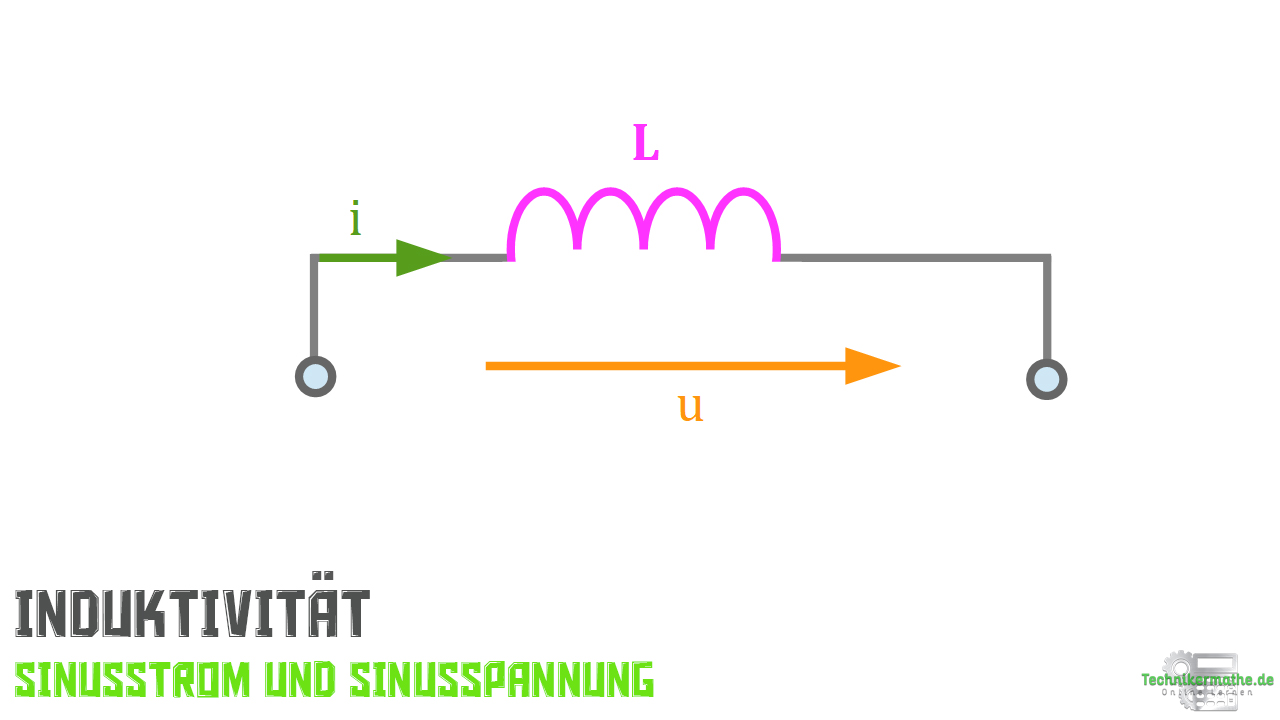
R-L-C-im-Wechselstrom - Schaltzeichen: Induktivität (Spule) im Schaltkreis — R-L-C-im-Wechselstrom – Schaltzeichen: Induktivität (Spule) im Schaltkreis

Die zugehörige Gleichung für die Berechnung der Spannung einer elektrischen Spule in einem Wechselstromkreis ist:

$u = L \cdot \frac{di}{dt}$

C | (Kondensator – Kapazität)

Nachfolgend siehst du das typische Schaltzeichen für einen elektrischen Kondensator:

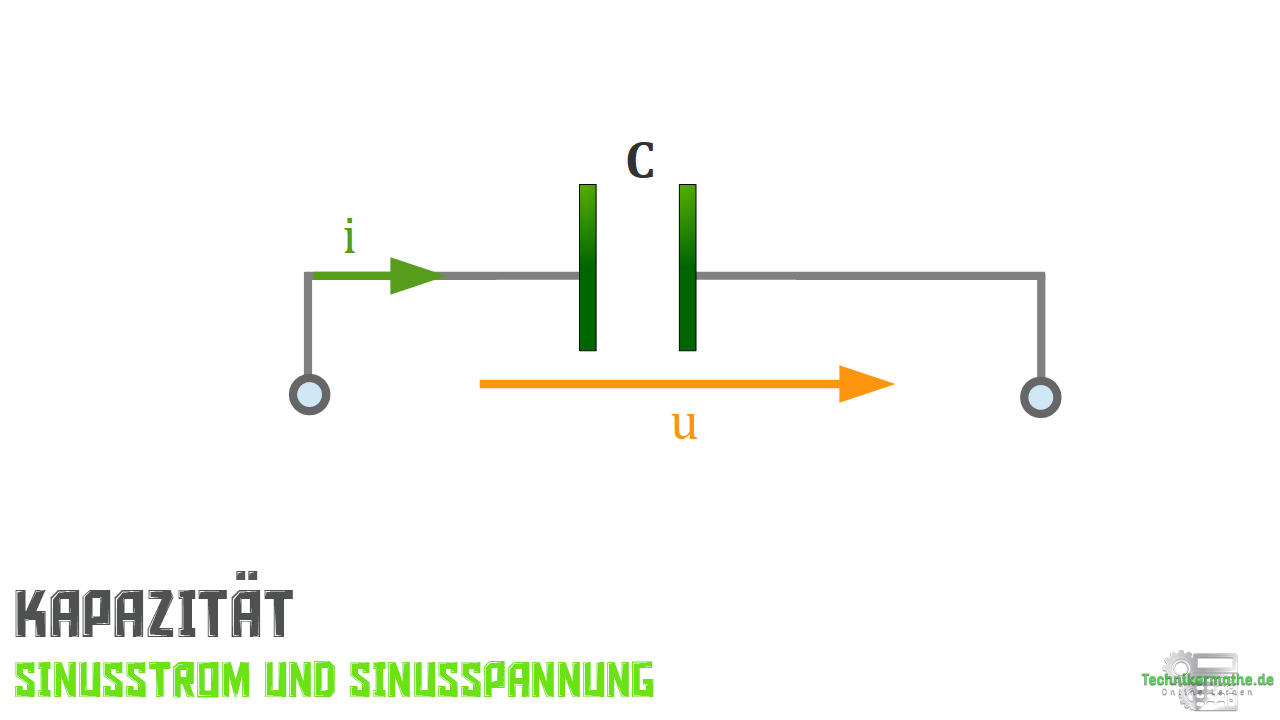
R-L-C-im-Wechselstrom - Schaltzeichen: Kapazität (Kondensator) im Schaltkreis — R-L-C-im-Wechselstrom – Schaltzeichen: Kapazität (Kondensator) im Schaltkreis

Die zugehörige Gleichung für die Berechnung der Spannung eines elektrischen Kondensators in einem Wechselstromkreis ist:

$u = \frac{1}{C} \cdot \int i dt$

R L C im Wechselstrom – Sinusspannung

Die Gleichung für die Sinusspannung kann wie folgt ausgedrückt werden

$u = \sqrt{2} U \cdot sin(\omega t)$

R L C im Wechselstrom – Sinusströme ermitteln

Um die Sinusströme zu ermitteln, bedienen wir uns der oben aufgeführten Gleichungen für die Berechnung der Spannungswerte im Wechselstromkreis.

“In der Realität würde man nun nacheinander an einen Widerstand, eine Spule und einen Kondensator eine Sinusspannung anlegen und anschließend den zugehörigen Strom ermitteln.”

Uns genügen jetzt aber erst mal die Gleichungen:

R | Ohm’scher Verbraucher – Widerstand – Sinusstrom (Herleitung + Formel)

Als Ausgangsgleichung dient uns die bereits erwähnte allgemeine Spannungsgleichung als Abwandlung des allgemeinen Ohm’schen Gesetzes.

$u = i \cdot R$

Diese Gleichung können wir jetzt ganz easy nach $i$ auflösen, indem wir beide Seiten der Gleichung durch $R$ dividieren.

$i = \frac{u}{R}$

Da es sich bei der Spannung um eine Sinusspannung handelt müssen wir diese Gleichung aber noch anpassen:

$i = \frac{u}{R} = \sqrt{2} \frac{U}{R} \cdot sin (\omega t)$

L | Spule – Induktivität – Sinusstrom (Herleitung + Formel)

Als Ausgangsgleichung dient uns die bereits erwähnte allgemeine Spannungsgleichung für die Spule.

$u = L \cdot \frac{di}{dt}$

Diese Gleichung können wir jetzt ganz easy nach $i$ auflösen.

$i = \frac{1}{L} \int u \cdot dt$

Da es sich bei der Spannung um eine Sinusspannung handelt müssen wir diese Gleichung aber noch anpassen:

$i = - \sqrt{2} \frac{U}{\omega \cdot L} \cdot cos (\omega t)$

“Noch haben wir aber für die Spule keine Sinusfuktion, sondern lediglich eine Kosinusfunktion vorliegen.”

C | Kondensator – Kapazität – Sinusstrom (Herleitung + Formel)

Als Ausgangsgleichung dient uns die bereits erwähnte allgemeine Spannungsgleichung für den Kondensator.

$u = \frac{1}{C} \int i dt$

Diese Gleichung können wir jetzt ganz easy nach $i$ auflösen.

$i = C \frac{du}{dt}$

Da es sich bei der Spannung um eine Sinusspannung handelt müssen wir diese Gleichung aber noch anpassen:

$i = \sqrt{2} U \cdot \omega \cdot C \cdot cos (\omega t)$

“Noch haben wir aber für die Kapazität keine Sinusfuktion, sondern lediglich eine Kosinusfunktion vorliegen.”

R L C im Wechselstrom – Zweckmäßige Anpassung der Größen

Wir passen die Größen nun in zweierlei Hinsicht an.

Anpassung der Kurzzeichen

Die Kurzzeichen für die Sinusströme / Kosinusströme erhalten ein tiefergestelltes Symbol, damit man sie in umfangreichen Berechnungen auch direkt identifizieren kann.

$i_R = \frac{u}{R} = \sqrt{2} \frac{U}{R} \cdot sin (\omega t)$

$i_L = - \sqrt{2} \frac{U}{\omega \cdot L} \cdot cos (\omega t)$

$i_C = \sqrt{2} U \cdot \omega \cdot C \cdot cos (\omega t)$

R L C im Wechselstrom – Transformation der Kosinusfunktion in eine Sinusfunktion

Da es sich bei der Gleichung für die Induktivität und die Kapazität jeweils um eine Kosinusfunktion handelt, müssen wir einen Umrechnungsfaktor ermitteln, der es uns erlaubt daraus eine Sinusfunktion zu erzeugen.

Der notwendige Umrechnungsfaktor ist

$- cos(\omega t) = sin(\omega t - \frac{\pi}{2})$

$i_R = \frac{u}{R} = \sqrt{2} \frac{U}{R} \cdot sin (\omega t)$ (Diese Gleichung bleibt unverändert, ist bereits eine Sinusfunktion)

$i_L = - \sqrt{2} \frac{U}{\omega \cdot L} \cdot sin(\omega t - \frac{\pi}{2})$ (Es findet ein Vorzeichenwechsel statt)

$i_C = \sqrt{2} U \cdot \omega \cdot C \cdot sin(\omega t - \frac{\pi}{2})$ (Es findet ein Vorzeichenwechsel statt)

Was kommt als Nächstes?

Nachdem wir jetzt die Größen R L C im Wechselstrom eingeführt haben und die die zugehörigen Sinusströme und Sinusspannungen kennengelernt hast, wollen wir im kommenden Kurstext auf das Thema Blindwiderstände und Leitwerte näher eingehen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++