In dieser Lerneinheit starten wir mit dem Zeigerdiagramm. Obwohl wir dieses Thema noch ausführlich behandeln, möchten wir dir jetzt aufführen, warum sich Zeigerdiagramme häufig besser zur Beurteilung von Sinusgrößen eignen als Zeitdiagramme. Dabei stellen wir u.A. auch Begriffe wie die Projektion vor.
Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema. Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET6-Wechselstromtechnik 1 Die Vertiefung der Wechselstromtechnik findest du im Kurs: ET7-Wechselstromtechnik 2
Wenn man Sinusgrößen ordentlich darstellen möchte, so lässt sich dies mit Zeigerdiagrammen elegant realisieren.
Zeigerdiagramme – Grundlagen zu Sinusstrom und Sinusspannung
Wenn man Sinusgrößen ordentlich darstellen möchte so kann man dies mit Zeigerdiagrammen realisieren. Vielleicht denkst du dir jetzt, was soll das, bisher haben wir die Sinusgrößen doch als Sinuslinien über der Zeit t aufgetragen. Das stimmt zwar aber hier gilt auch, dass
Je mehr Sinusgrößen man gleichzeitig betrachten möchte, umso unübersichtlicher sind die Zeitdiagramme.
Die Darstellung von Zeitdiagrammen für Sinusgrößen ist nachfolgend dargestellt:
Sinusspannung im Zeitdiagramm
Nachfolgend siehst du die Darstellung einer Sinusspannung im Zeitdiagramm (!).
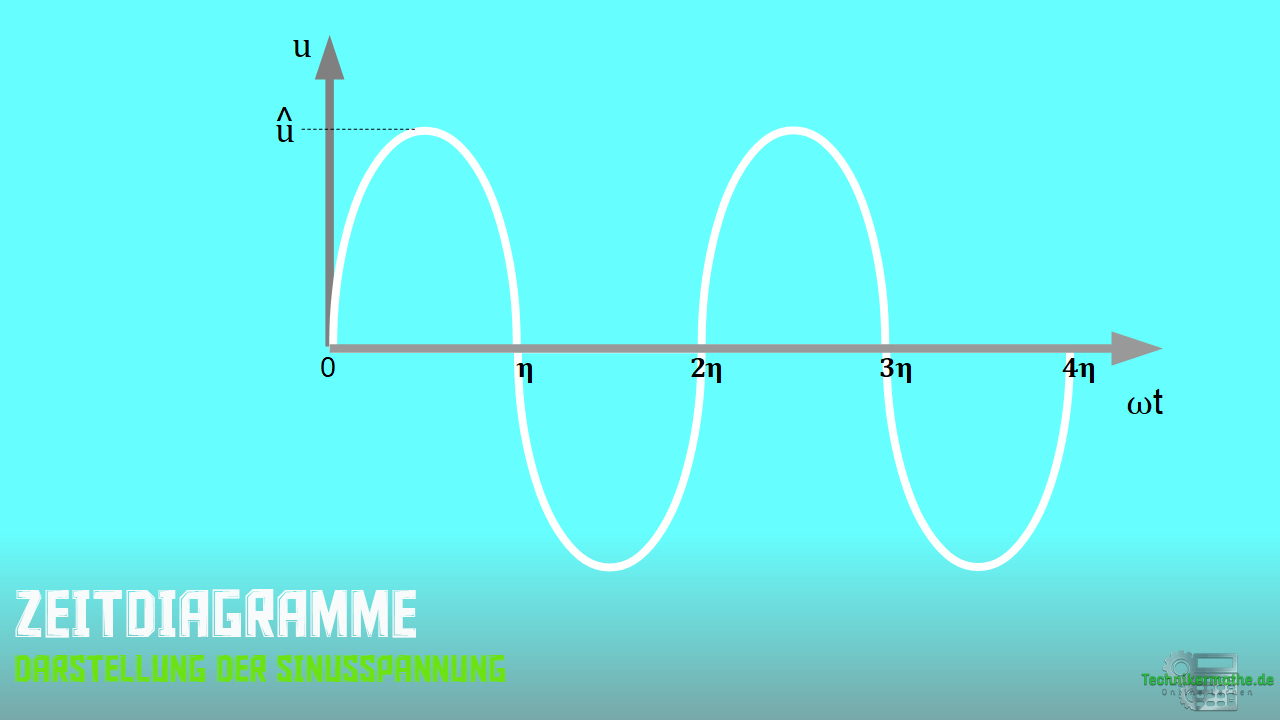
Sinusspannung im Zeigerdiagramm
Nachfolgend siehst du die Darstellung einer Sinusspannung im Zeigerdiagramm (!).
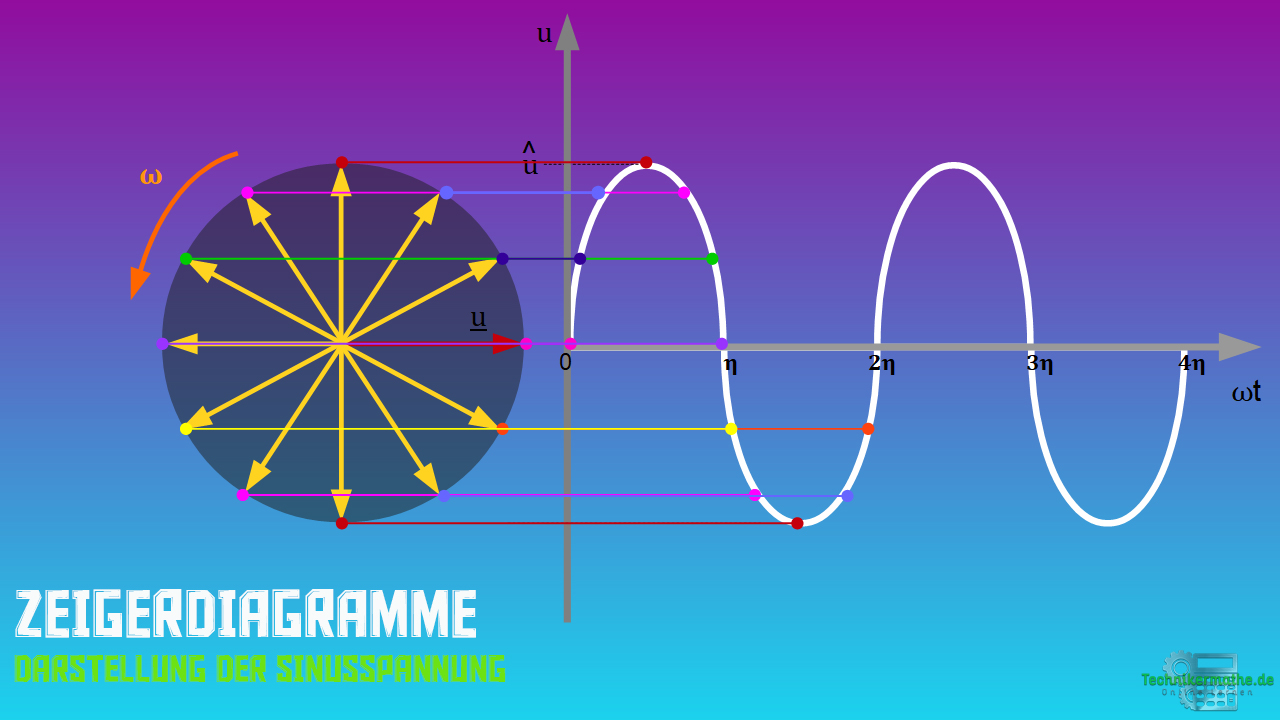
Darstellung eines Sinusstroms im Zeitdiagramm
Nachfolgend siehst du die Darstellung eines Sinusstroms im Zeitdiagramm.
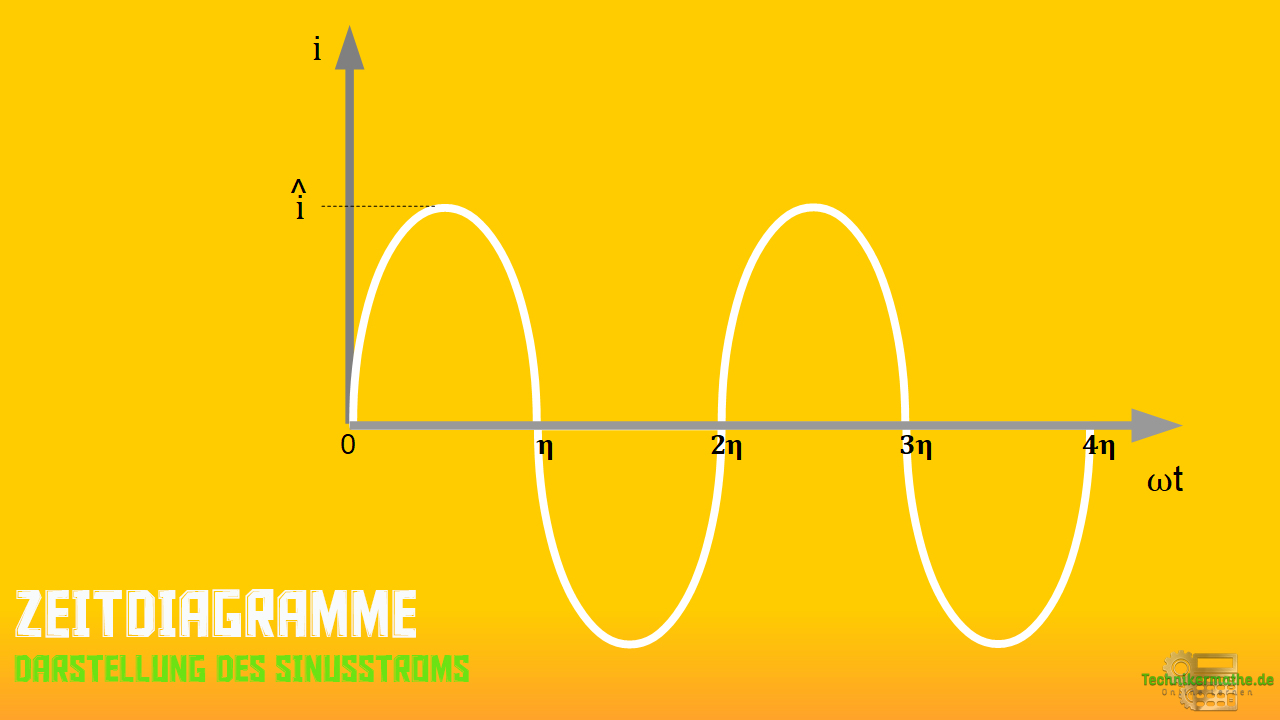
Darstellung eines Sinusstroms im Zeigerdiagramm
Nachfolgend siehst du die Darstellung eines Sinusstroms im Zeigerdiagramm.
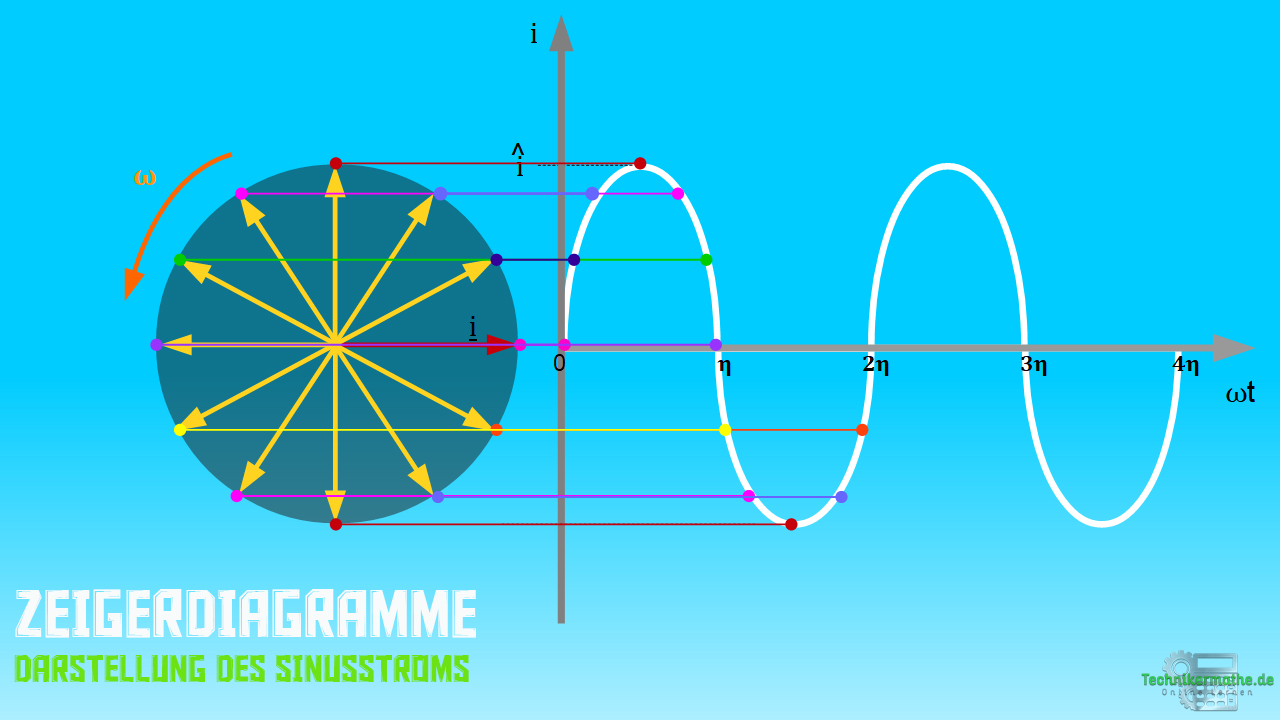
Mit den Zeigerdiagrammen kann man also sinusförmige zeitabhängige Größen wie den Strom [i(t)] und die Spannung [u(t)] einfach und auf symbolische Weise darstellen.
Zeigerdiagramme – Bestandteile / Größen
Ähnlich wie bei der Aufnahme eines Fotos mit einer Kamera, können wir mit dem Zeigerdiagramm immer nur Momentaufnahmen der sich drehenden Zeiger von Strom und Spannung machen, da es sich ja um feststehende Zeiger handelt.
Zeiger im Diagramm
Zuerst sollten wir klären was ist überhaupt ein Zeiger:
Ein Zeiger ist ein Einfachpfeil, der vom Ursprung ausgehend den Scheitelwert der jeweiligen Sinusgröße angibt.
Da wir Ströme und Spannungen unterscheiden gilt:
- Bei einem sinusförmigen Strom entspricht die Zeigerlänge dem Scheitelwert
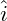oder dem Effektivwert 
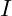. - Bei einer sinusförmigen Spannung entspricht die Zeigerlänge dem Scheitelwert
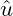oder dem Effektivwert 
.
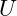Damit wir aber überhaupt wissen ob es sich um einen Strom oder um eine Spannung handelt versehen wir den Zeiger mit einem einem unterstrichenen 
für einen Strom oder einem unterstrichenen 
für eine Spannung.
Der Unterstrich ist notwendig, damit wir direkt wissen, dass hier nicht allein eine physikalische Größe, sondern auch die Eigenschaft des Zeigers betrachtet werden soll.
Winkelgeschwindigkeit
Die Winkelgeschwindigkeit 
ist die Geschwindigkeit mit der sich der Zeiger im mathematisch positiven Sinn, also entgegen dem Uhrzeigersinn, rotierend um den Koordinatenursprung bewegt.
Es ist das gleiche Prinzip wie bei einer verkehrt herum laufenden Uhr. Diese Größe wird auch fast immer bei Darstellungen mit eingetragen.
Dreht sich der Zeiger gleichmäßig so entspricht die Winkelgeschwindigkeit des Zeigers der Kreisfrequenz der Sinusschwingung.
Kennzahlen:
Winkelgeschwindigkeit
Kreisfrequenz
Kreiszahl
Frequenz
Projektion der Zeigerspitze
Durch die Drehung des Zeigers ist die Projektion der Zeigerpitze auf die ruhende Zeitlinie 
der Zeitwert 
.
Formal ausgedrückt heißt das:
Kennzahlen
Zeitwert
Scheitelwert
Winkelgeschwindigkeit
Eine im Zeitdiagramm dargestellte Sinuskurven von Strom oder Spannung ist als Projektion eines sich gleichmäßig drehenden Zeigers auch als stillstehende Zeitlinie darstellbar.
Zeiger in Zeigerdiagrammen – Kennwerte
Sowohl die Sinusschwingung als auch die zugehörigen Zeiger können durch vier Kennwerte genau und eindeutig beschrieben werden.
Art der Sinusgröße
Ob sich um eine Sinusspannung oder um einen Sinusstrom handelt, wird mit Hilfe von oder gekennzeichnet. Noch mal fürs Gedächtnis: Der Unterstrich steht für den Zeigercharakter der Größe.
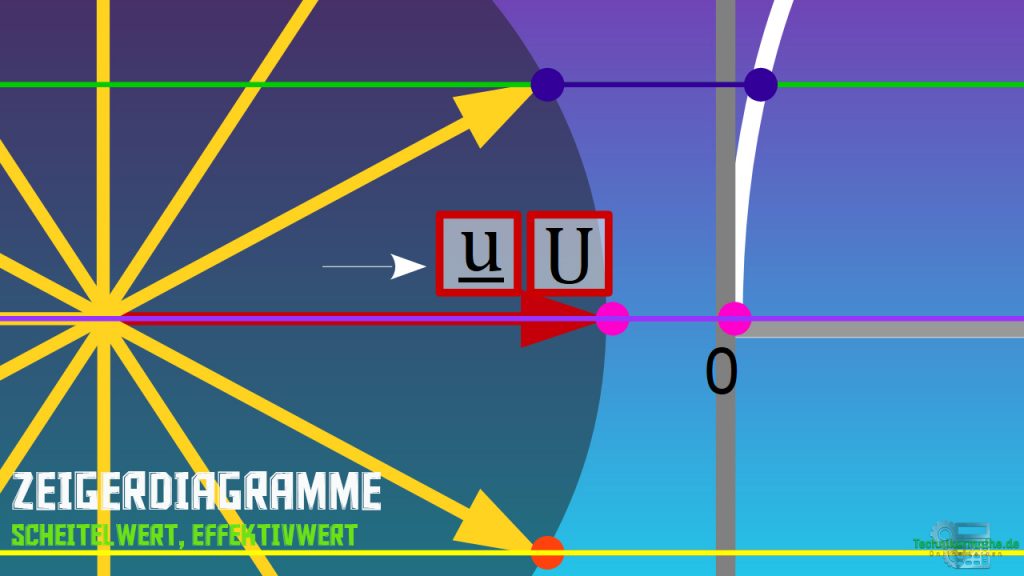
Betrag der Sinusgröße
Die Länge des Zeigers gibt uns Auskunft darüber. Entweder verwenden wir die Angabe der Scheitelwerte 
und 
oder die Wahl fällt auf die Angabe der Effektivwerte 
und 
. Damit nicht geschätzt werden muss, legen wir einen Maßstab fest. Dieser kann z.B. beim einem Sinusstrom 
oder bei einer Sinusspannung 
entsprechend. Je nach Größe sollte man den Maßstab anders setzen.
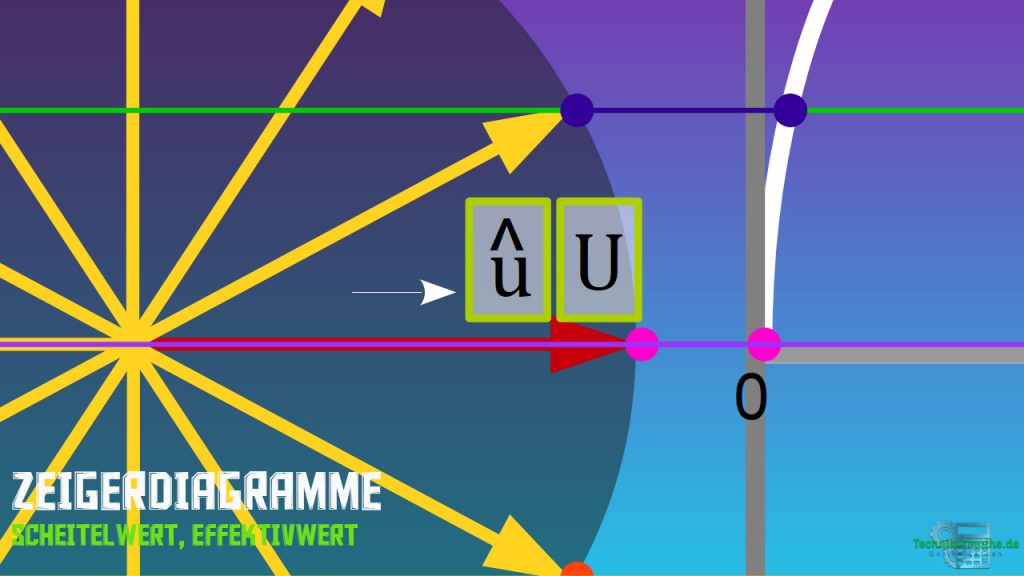
Phasenlage der Sinusgröße
Liegen mehrere gleichfrequente Sinusgrößen vor, so können wir diese mit Hilfe der Phasenlagen voneinander unterscheiden. Im Zeigerdiagramm entspricht die Phasenlage dem Phasenwinkel 
zwischen zwei Zeigern. Wie sich das äußert siehst du in der nachfolgenden Abbildung.
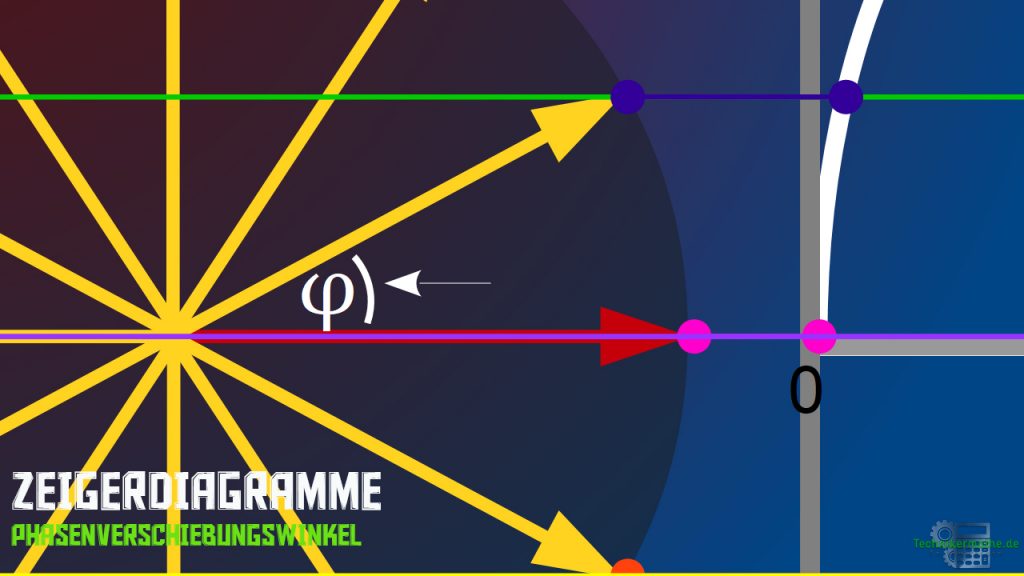
Frequenz der Sinusschwingung
Die Frequenz ist der Ausgangswert für die Winkelgeschwindigkeit des sich drehenden Zeigers. Hier zeigt sich auch die Einschränkung von Zeigerdiagrammen denn Zeigerdiagramme können nur gleichfrequente Verläufe von Sinuskurven darstellen.
Zeigerdiagramme – Drehzeiger, Scheitelwertzeiger
Die Verwendung eines Drehzeigers für die Erstellung eines Zeitdiagramms aus dem Zeigerdiagramm ist nützlich und zur Bestimmung des Zeitwertes sogar erforderlich.
Es ist sinnig die für die Beschreibung der Abhängigkeiten der Sinusgrößen untereinander, also der sich drehenden Zeiger, einen sich mitbewegenden Standpunkt zu suchen.
Somit stehen für uns als Beobachter, der sich mit der gleichen Winkelgeschwindigkeit wie die Zeiger bewegt, die Zeiger still. Unser Blick auf die Zeiger variiert mit unser Winkelposition, weshalb diese als willkürlich angenommen werden muss.
Überhaupt nicht willkürlich sondern festgelegt sind die Winkel zwischen den Zeigern. Hier erhalten wir Zeiger, die in der Bildebene feststehen. Man bezeichnet sie als ruhende Scheitelwertzeiger.
Da wir Ströme und Spannungen unterscheiden gilt:
- Bei einem sinusförmigen Strom wird der ruhende Scheitelwertzeiger mit einem Dach und Unterstrich gekennzeichnet
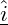
- Bei einer sinusförmigen Spannung wird der ruhende Scheitelwertzeiger mit einem Dach und Unterstrich gekennzeichnet
Nachdem du jetzt weißt was ein Zeigerdiagramm ist und in welchem Zusammenhang es mit dem Zeitdiagramm steht, möchten wir dir im kommenden den Phasenverschiebungswinkel vorstellen. Übrigens es war nicht das letzte Mal, dass wir uns mit Zeigerdiagrammen beschäftigen. Eine noch genauere Betrachtung mit Zahlenwerten folgt in einem späteren Abschnitt.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben
Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team
