(ET5-041) – Phasenwinkel und Nullphasenwinkel

In diesem Kurstext stellen wir dir mit dem Phasenwinkel und dem Nullphasenwinkel für einen Sinusstrom und eine Sinusspannung die ersten wichtigen Winkel in der Wechselstromtechnik vor.

Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET6-Wechselstromtechnik 1

Die Vertiefung der Wechselstromtechnik findest du im Kurs: ET7-Wechselstromtechnik 2

Merk’s dir!

“Eine Wechselspannung kann man als sin– oder cos-Funktion in Abhängigkeit der Zeit t darstellen. Wir betrachten beide Varianten.”

Phasenwinkel – Grundlegendes

Die Phase oder besser gesagt dessen Winkel gibt uns Auskunft darüber, wo sich in Sinusstrom oder eine Sinusspannung aktuell in einem periodischen Vorgang (Periodendauer T) befinden.

Da es sich um sinusförmige Verläufe handelt ist die Phase, jene Größe von der die Winkelfunktion direkt abhängt.

Phasenwinkel – Zeigerbild

Im Zeigerdiagramm/Zeigerbild kann man eine harmonische Schwingung direkt mit einem Zeiger veranschaulichen, welcher sich gegen den Uhrzeigersinn mit einer konstanten Winkelgeschwindigkeit um den Koordinatenursprung dreht. Die x-Achse stellt hier den positiven Nulldurchgang dar. Es handelt sich also um den Startpunkt für $t = 0$

Die Thematik der Zeigerbilder, sowie deren Erstellung folgt noch als Einzelthema später im Kurs

Zeigerbild – Kosinusstrom

Nachfolgend siehst du die Darstellung für den Kosinusstrom $i$ .

Kosinusstrom im Zeigerdiagramm [1. Quadrant]

Zeigerbild – Kosinusspannung

In der zweiten Abbildung findest du die Darstellung für die Kosinusspannung $u$

Kosinusspannung im Zeigerdiagramm [1. Quadrant]

Merk’s dir!

Den Winkel zwischen dem Zeiger und der horizontalen Achse des Koordinatensystems bezeichnen wir als Phasenwinkel $\varphi$ .

Ausgehend von den obigen Abbildungen kannst du erkennen, dass der Winkel mit der Zeit zunimmt.

Phasenwinkel – Funktionen – Strom und Spannung

Zuerst stellen wir dir die allgemeine Form von beiden Funktionen vor und anschließend die zugehörigen von Strom und Spannung.

Sinusfunktion und Kosinusfunktion – Allgemeine Form

Sinusfunktion

$x (t) = \hat{x}\cdot sin(\varphi (t)) = \hat{x}\cdot sin(\omega \cdot t + \varphi_0)$

Kosinusfunktion

$x (t) = \hat{x}\cdot cos(\varphi (t)) = \hat{x}\cdot cos(\omega \cdot t + \varphi_0)$

Kennzahlen:

$\varphi (t) =$ Phasenwinkel (= Ph.winkel)

$\omega =$ Kreisfrequenz (Konstante)

$\varphi_0 =$ Nullphasenwinkel ( NPh.winkel, Phasenwinkel zum Zeitpunkt t = 0)

$\omega = 2 \pi f = \frac{2\pi}{T}$

Kennzahlen:

$f =$ Frequenz

$T =$ Periodendauer

Nachfolgend findest du die Sinusfunktionen und die Kosinusfunktionen für den Strom und die Spannung.

Sinusfunktion – Strom und Spannung

Nachfolgend findest du die Sinusfunktionen für den Strom und die Spannung

Elektrischer Strom – Formel

Als erstes Stellen wir dir Sinusfunktion für den elektrischen Strom auf. Diese sieht wie folgt aus:

$i (t) = \hat{i}\cdot sin(\varphi (t)) = \hat{i}\cdot sin(\omega \cdot t + \varphi_{0i})$

Kennzahlen:

$\varphi (t) =$ Ph.winkel

$\omega =$ Kreisfrequenz (Konstante)

$\varphi_{0i} =$ NPh.winkel (= Phasenwinkel zum Zeitpunkt t = 0)

$\omega = 2 \pi f = \frac{2\pi}{T}$

Kennzahlen:

$f =$ Frequenz

$T =$ Periodendauer

Elektrische Spannung – Formel

Jetzt stellen wir die Sinusfunktion für die elektrische Spannung auf. Diese hat folgende Form:

$u (t) = \hat{u}\cdot sin(\varphi (t)) = \hat{u}\cdot sin(\omega \cdot t + \varphi_{0u})$

Kennzahlen:

$\varphi (t) =$ Ph.winkel

$\omega =$ Kreisfrequenz (Konstante)

$\varphi_{0u} =$ NPh.winkel ( = Phasenwinkel zum Zeitpunkt t = 0)

$\omega = 2 \pi f = \frac{2\pi}{T}$

Kennzahlen:

$f =$ Frequenz

$T =$ Periodendauer

Kosinusfunktion – Strom und Spannung

Nachfolgend findest du die Kosinusfunktionen für den Strom und die Spannung.

Elektrischer Strom – Formel

Die Kosinusfunktion für den elektrischen Strom hat folgende Erscheinung:

$i (t) = \hat{i}\cdot cos(\varphi (t)) = \hat{i}\cdot cos(\omega \cdot t + \varphi_{0i})$

Kennzahlen:

$\varphi (t) =$ Ph.winkel

$\omega =$ Kreisfrequenz (Konstante)

$\varphi_{0i} =$ NPh.winkel ( Phasenwinkel zum Zeitpunkt t = 0)

$\omega = 2 \pi f = \frac{2\pi}{T}$

Kennzahlen:

$f =$ Frequenz

$T =$ Periodendauer

Elektrische Spannung – Formel

Zu guter Letzt noch die Kosinusfunktion der elektrischen Spannung:

$u (t) = \hat{u} \cdot cos(\varphi (t)) = \hat{u}\cdot cos(\omega \cdot t + \varphi_{0u})$

Kennzahlen:

$\varphi (t) =$ Ph.winkel

$\omega =$ Kreisfrequenz (Konstante)

$\varphi_{0u} =$ NPh.winkel ( Phasenwinkel zum Zeitpunkt t = 0)

$\omega = 2 \pi f = \frac{2\pi}{T}$

Kennzahlen:

$f =$ Frequenz

$T =$ Periodendauer

Nullphasenwinkel – Nulldurchgang

Wir betrachten nun zwei mögliche Fälle:

Nullphasenwinkel – Startpunkt nicht positiver Nulldurchgang

Liegt uns ein Fall vor, bei dem wir unsere Betrachtung mit $t = 0$ startet, jedoch für den Sinusstrom oder die Sinusspannung nicht beim positiven Nulldurchgang beginnt. Können wir diese Verschiebung mit dem Nullphasenwinkel kennzeichnen.

Der Nullphasenwinkel ist für den Sinusstrom $i$ dann $0 < \varphi_{0i} < \pi$ und für die Sinusspannung $u$ gleich $0 < \varphi_{0u} < \pi$ .

Nullphasenwinkel – Startpunkt positiver Nulldurchgang

Wenn jedoch der Fall auftritt, dass wir unsere Betrachtung mit $t = o$ starten und der Startpunkt für den Sinusstrom oder die Sinusspannung der positive Nulldurchgang ist, so sind $\varphi_{0i} = 0$ und $\varphi_{0u} = 0$

Nullphasenwinkel – Messung

Was soll das?…

Man bestimmt diesen Winkel, da die zeitliche Verschiebung des Sinusstroms und der Sinusspannung vom positiven Nulldurchgang ebenfalls durch einen Winkel dargestellt wird.

Merk’s dir!

Die Angabe des Winkels kann in Bogenmaß oder in Gradmaß erfolgen. Ermittelt werden kann der Winkel mit einem Zweistrahloszillograf, sofern eine frequenzgleiche Vergleichsspannung bzw. frequenzgleicher Vergleichsstrom zugrunde gelegt wird. Deren Nullwinkel müssen dann

$\varphi_{0uv} = 0 rad$

sowie

$\varphi_{oiv} = 0 rad$

betragen.

Die sinusförmige Spannung, deren Nullwinkel 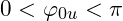$0 < \varphi_{0u} < \pi$ beträgt ist auf der Zeitachse gegenüber der Spannung mit dem Nullphasenwinkel $\varphi_{0uv} = 0 rad$ um die entsprechende Zeit $0 < t < \frac{T}{2}$ nach links verschoben.

Der sinusförmige Strom, deren Nullwinkel 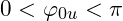$0 < \varphi_{0u} < \pi$ beträgt ist auf der Zeitachse gegenüber dem Strom mit dem Nullphasenwinkel $\varphi_{0iv} = 0 rad$ um die entsprechende Zeit $0 < t < \frac{T}{2}$ nach links verschoben.

Phasenwinkel – Relevanz

Es gibt unterschiedliche Fälle in denen der Winkel benötigt wird. Hier sind zwei Fälle (einer aus der Wechselstromtechnik und einer aus der Drehstromtechnik)

Der Winkel hilft bei der Bestimmung von Wechselstromwiderständen, wenn Wechselspannung und Wechselstrom gegeneinander in Phasen verschoben sind.
Der Winkel hilft auch in der Drehstromtechnik, denn hier sind die Spannungsschwingungen in den drei Leitungen um jeweils 120° verschoben.

Was kommt als Nächstes?

Nachdem du jetzt den (Null)Phasenwinkel und die zugehörigen Zeigerbilder kennengelernt hast, möchten wir uns im kommenden Kurstext den Belastungsarten Widerstand R, Induktivität L sowie Kapazität C im Wechselstromkreis zuwenden. Diese werden dir im Kurs an unterschiedlichen Stellen wieder begegnen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++