(ET5-04) Wechselstromtechnik – Wechselgrößen [Crestfaktor, Formfaktor, etc.]

In dieser Lerneinheit stellen wir dir weitere wichtigsten Größen für die Wechselgrößen aus der Wechselstromtechnik vor. Dabei sind Größen wie Scheitelwert, Gleichrichtwert, Effektivwert sowie die Faktoren Crestfaktor und Formfaktor vor.

Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET6-Wechselstromtechnik 1

Die Vertiefung der Wechselstromtechnik findest du im Kurs: ET7-Wechselstromtechnik 2

Merk’s dir!

“Die Wechselstromgrößen und Wechselspannungsgrößen kennzeichnet, dass sie einer zeitlichen Änderung unterworfen sind.”

Wechselgrößen - Effektivwert, Gleichrichtwert, Scheitelwert — Wechselgrößen – Effektivwert, Gleichrichtwert, Scheitelwert

Wechselgrößen – Grundlagen

Du hast bereits mit dem elektrischen Strom $i$ und der elektrischen Spannung $u$ sowie den zugehörigen arithmetischen Mittelwerten $\overline{i}$ und $\overline{u}$ , die wichtigsten Wechselgrößen kennengelernt. Strom und Spannung verhalten sich periodisch, wodurch ihre arithmetischer Mittelwerte für eine vollständige Periodendauer $T$ den Wert null annehmen.

Nachfolgend noch mal die beiden Gleichungen:

Elektrischer Strom – Arithmetischer Mittelwert

$\overline{i} = \frac{1}{T} \int_{0}^{T} i(t) dt = 0$

Kennzahlen:

$\overline{i} =$ Arithmetischer Mittelwert

$T =$ Periodendauer

$i(t) =$ Augenblickwert des Stroms.

Elektrische Spannung – Arithmetischer Mittelwert

$\overline{u} = \frac{1}{T} \int_{0}^{T} u(t) dt = 0$

Kennzahlen:

$\overline{u} =$ Arithmetischer Mittelwert

$T =$ Periodendauer

$u(t) =$ Augenblickwert der Spannung.

Leider eignet sich der arithmetische Mittelwert nicht um eine Wechselgröße eindeutig zu charakterisieren, da er halt immer den Wert null hat. Abhilfe schaffen hier weitere Kennwerte die eine quantitative und qualitative Aussage über eine Wechselgröße zulassen.

Wechselgrößen – Weitere Größen

Neben den beiden bekannten Größen ohne Aussagewert, können wir für unsere Untersuchung auch weitere Größen heranziehen, die uns wirklich Informationen abseits von 0 liefern. Nachfolgend behandelt wir deshalb:

Mischgrößen

sowie

Scheitelwert

sowie

Gleichrichtwert

sowie

Effektivwert

sowie die Faktoren

Crestfaktor

sowie

Formfaktor

Wechselgrößen – Mischgrößen

Eine Mischgröße der Wechselgrößen ist in der Wechselstromtechnik immer dann gegeben, wenn arithmetische Mittelwert einer periodischen Größe nicht den Wert null annimmt. In diesem Fall überlagert sich der Wert des arithmetischen Mittels mit einer Wechselgröße.

Wechselgrößen – Scheitelwert

Wie du weißt, bilden die Augenblickswerte von Strom und Spannung eine Kurve mit periodischen Verlauf, so wie in der nächsten Abbildung dargestellt:

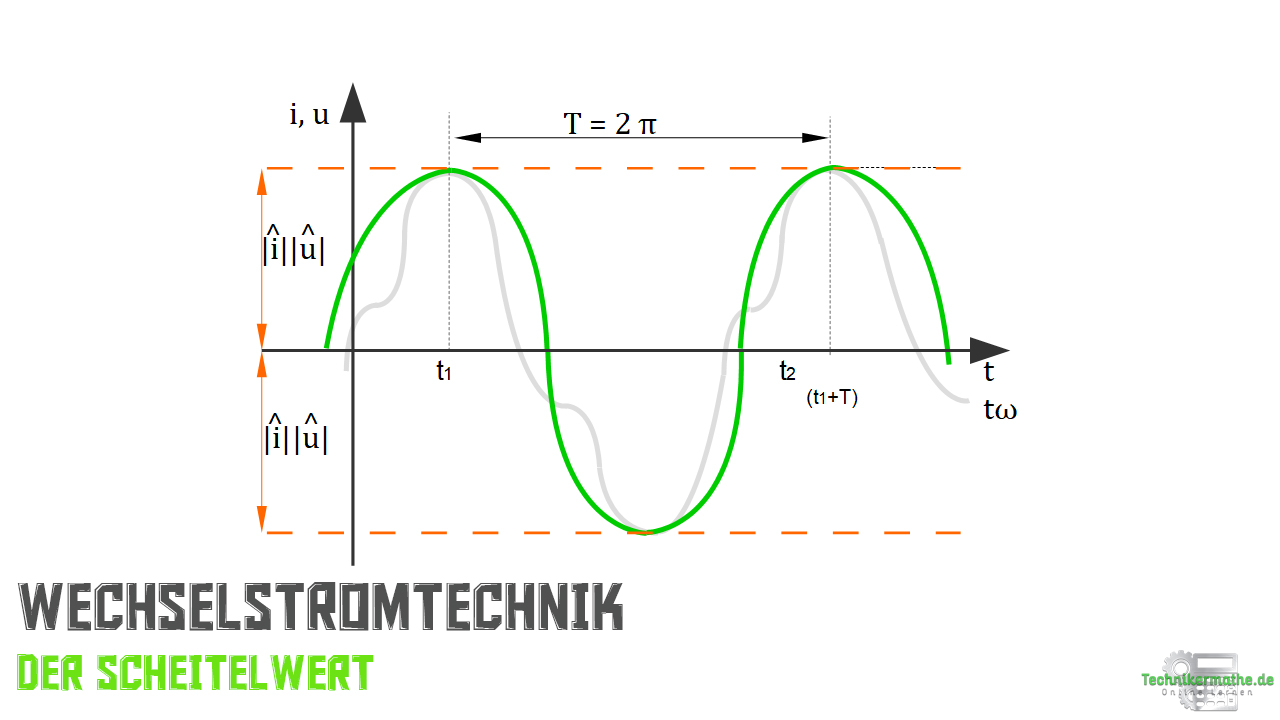
Dabei weist die Kurve immer einen Maximalwert und einen Minimalwert (zumeist negativen Wert) auf. Der Scheitelwert, auch in der Abbildung eingezeichnet, ist der Wert, welcher betragsmäßig am größten ist. Um auch negative Werte zu berücksichtigen, werden die Ergebnisse immer als Betrag angegeben, womit eine gesamtheitliche Vergleichbarkeit möglich wird. Formal sieht das dann wie folgt aus:

Scheitelwert – Strom (Formel + Einheit)

$\hat{i} = max(|i_{min}|, |i_{max}| > 0$

(Grundsätzlich kann man auch auf die Betragsstriche bei $i_{max}$ verzichten.)

Kennzahlen:

$\hat{i} =$ Scheitelwert des Stroms

$i_{min} =$ maximaler negativer Stromwert

$i_{max} =$ maximaler positiver Stromwert

Einheit

Die Einheit des Arithmetischen Mittelwerts des Stroms ist Ampere.

$[\hat{i}] = 1 A$

Scheitelwert – Spannung (Formel + Einheit)

$\hat{u} = max(|u_{min}|, |u_{max}| > 0$

(Auch hier gilt: Grundsätzlich kann man auch auf die Betragsstriche bei $u_{max}$ verzichten.)

Kennzahlen:

$\hat{u} =$ Scheitelwert der Spannung

$u_{min} =$ maximaler negativer Spannungswert

$u_{max} =$ maximaler positiver Spannungswert

Einheit

Die Einheit des Scheitelwerts der Spannung ist Volt.

$[\hat{u}] = 1 V$

Wechselgrößen – Gleichrichtwert

Der Gleichrichtwert von Wechselgrößen wie Wechselstroms oder Wechselspannung gibt uns Auskunft darüber, welcher Gleichstrom oder welche Gleichspannung dieselbe Ladungsmenge transportiert, wie im zeitlichen Mittel ein gleichgerichteter Wechselstrom.

In der nächsten Abbildung ist der Wert für den Strom und die Spannung eingezeichnet.

Merk’s dir!

Hierbei muss gelten, dass der Flächeninhalt beider oranger Flächen deckungsgleich sind. Wenn dem so ist, dann stimmt auch das Ergebnis!

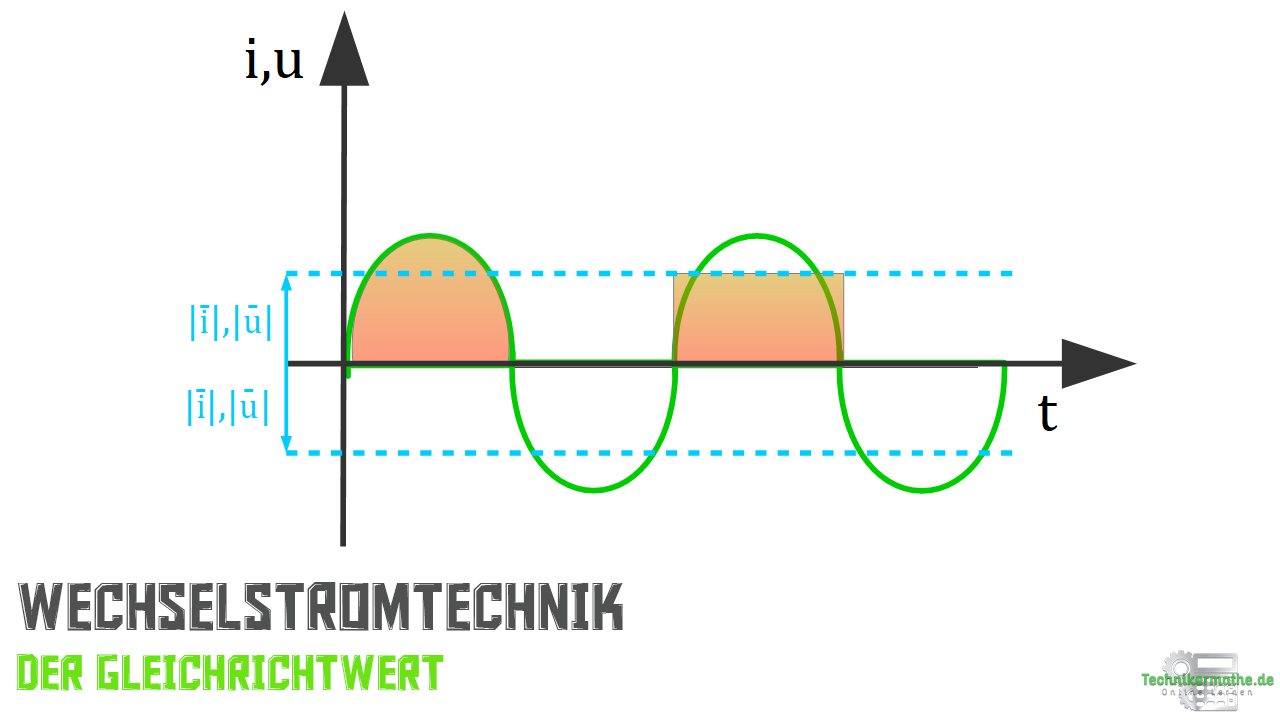
Wechselgrößen - Gleichrichtwert — Wechselgrößen – Gleichrichtwert

Das habe ich aber anders gelesen…

In der Literatur findest du noch die alternative Bezeichnung elektrolytischer Mittelwert.

Merk’s dir!

Der Gleichrichtwert steht für den mittleren Gleichstrom oder die mittlere Gleichspannung.

Sie eignet sich als qualitative und quantitative Größe, da sie im Gegensatz zum Arithmetischen Mittelwert nicht den Wert null annimmt. Das positive oder negative Ergebnis ist immer von null verschieben. Auch hier werden zu Vergleichszwecken Betragsstriche genutzt um eine Vergleichbarkeit zu gewährleisten.

Wie funktioniert’s?…

Wir betrachten hier die absoluten und somit Vorzeichen-freien Beträge. Diese addieren wir dann und dividieren deren Summe anschließend durch die Anzahl der Beträge (Summanden).

Gleichrichtwert – Strom (Formel + Einheit)

$|\overline{i}| = \frac{1}{T} \int_0^T |i(t)|dt$

Kennzahlen:

$\overline{i} =$ Gleichrichtwert

$i(t) =$ Augenblickswert zum Zeitpunkt t

$T =$ Periodendauer

Einheit

Die Einheit des Gleichrichtwerts des Stroms ist Ampere.

$[\hat{i}] = 1 A$

Gleichrichtwert – Spannung (Formel + Einheit)

$|\overline{u}| = \frac{1}{T} \int_0^T |u(t)|dt$

Kennzahlen:

$\overline{u} =$ Gleichrichtwert

$u(t) =$ Augenblickswert zum Zeitpunkt t

$T =$ Periodendauer

Einheit

Die Einheit des Gleichrichtwerts der Spannung ist Volt.

$[\hat{u}] = 1 V$

Gleichrichtwert – Strom + Spannung (Näherungsverfahren)

Für den Fall, dass man den Verlauf der Kurven nur mit höchsten Aufwand mathematisch beschreiben kann, lässt sich alternativ das wesentlich einfachere Näherungsverfahren nutzen.

Strom – Näherungsverfahren

$|\overline{i}| \aprox \frac{1}{n} \sum_{j=1}^n |i_j| = \frac{1}{n} (|i_1| + |i_2| + |i_3| + |i_4| +..... |i_n|)$

Spannung – Näherungsverfahren

$|\overline{u}| \aprox \frac{1}{n} \sum_{j=1}^n |i_j| = \frac{1}{n} (|i_1| + |i_2| + |i_3| + |i_4| +..... |i_n|)$

Wechselgrößen – Effektivwert

Der Effektivwert, nicht selten auch RMS-Wert (root mean square) genannt, ist der quadratische Mittelwert eines periodischen Signals. Wie der Name es eigentlich schon verrät, ist er der leistungswirksamste Wert eines periodischen Signals und somit die wichtigste Kenngröße eines Wechselstroms und einer Wechselspannung.

Im Normalfall werden alle Ströme und Spannungen in der Wechselstromtechnik als Effektivwerte angegeben.

Wenn beispielsweise die Netzwechselspannung den Wert 230 V aufweist, dann ist damit der Effektivwert der Netzwechselspannung gemeint.

Wie muss ich mir das vorstellen?…

Um ein Gefühl dafür zu bekommen, was den Effektivwert überhaupt auszeichnet, merke dir die folgende Definition:

Der Effektivwert eines Wechselstroms ist der Wechselstrom, welcher in einem Ohmschen Widerstand die gleiche Stromwärme bewirkt, wie ein Gleichstrom mit dem gleichen Betrag!

So ist die elektrische Leistung das Produkt aus Spannung und Strom. In unseren Diagrammen verläuft die Leistungskurve für symmetrische Sinuskurven von Wechselstrom und Wechselspannung nur im positiven Bereich.

Dabei liegt eine doppelte Frequenz vor. Aus mathematischer Sicht berechnet sich der Effektivwert aus der Quadratwurzel des Mittelwerts der Leistungskurve über eine Periode $T$ . Die Höhe des Effektivwerts richtet sich nach dem Scheitelwert und der Kurvenform.

Effektivwert – Leistung (Formel + Einheit)

$P = U \cdot I$

Kennzahlen:

$P =$ Leistung,

$u(t) =$ Augenblickswert zum Zeitpunkt t,

$T =$ Periodendauer.

Einheit

Die Einheit der Leistung ist Watt.

$[W] = 1 W$

Effektivwert – Strom (Formel + Einheit + Zeitfunktion)

$I = I_{eff} = \sqrt{ \frac{1}{T} \int_{0}^{T} i(t)^2 dt}$

Kennzahlen:

$I =$ Effektivwert des Stroms

$i(t) =$ Augenblickswert zum Zeitpunkt t

$T =$ Periodendauer

Einheit

Die Einheit des Effektivwerts des Stroms ist Ampere.

$[I] = 1 A$

Zeitfunktion

Die Zeitfunktion des Sinusstroms $i$ berechnet sich mit folgender Gleichung:

$i = \hat{i} sin \omega t$

Effektivwert mit Zeitfunktion

Der Effektivwert des Sinusstroms ist gegeben durch folgende Gleichung:

$I = \frac{\hat{i}}{\sqrt{2}} = 0,707 \hat{i}$

Hier wurde die Zeitfunktion des Stroms eingesetzt.

Effektivwert – Spannung (Formel + Einheit + Zeitfunktion)

$U = U_{eff} = \sqrt{ \frac{1}{T} \int_{0}^{T} u(t)^2 dt}$

Kennzahlen:

$I =$ Effektivwert der Spannung

$u(t) =$ Augenblickswert zum Zeitpunkt t

$T =$ Periodendauer

Einheit

Die Einheit des Effektivwerts des Stroms ist Volt.

$[I] = 1 V$

Zeitfunktion

Die Zeitfunktion der Sinusspannung $u$ berechnet sich mit folgender Gleichung:

$u = \hat{u} sin \omega t$

Effektivwert mit Zeitfunktion

Der Effektivwert der Sinusspannung ist gegeben durch folgende Gleichung:

$U = \frac{\hat{u}}{\sqrt{2}} = 0,707 \hat{u}$

Hier wurde die Zeitfunktion der Spannung eingesetzt.

Merk’s dir!

Als Formelzeichen schreibt man $I$ oder $I_{eff}$ , sowie $U$ oder $U_{eff}$ wobei der Index meistens nicht geschrieben wird.

Man benennt die Wechselgrößen nach den Effektivwerten. Messen kann man diese jeweils mit einem Strommesser, Spannungsmesser oder gleich beide zusammen mit einem Multimeter.

Die Augenblickwerte $i(t)$ und $u(t)$ hingegen können mit Hilfe eines Oszilloskops visualisiert werden.

Wechselgrößen – Faktoren

Jetzt stellen wir dir noch 2 Faktoren aus der Wechselstromtechnik vor.

Wechselgrößen – Crestfaktor

Als vorletzte Größe im Zusammenhang mit Wechselgrößen möchten wir dir nun den Crestfaktor vorstellen. Dieser gibt das Verhältnis von Scheitelwert zu Effektivwert an. Der Wert des Faktors wird von der Signalform bestimmt und ist größer oder gleich 1.

Angegeben wird der Crestfaktor immer mit dem Formelzeichen $\xi$ , hierbei handelt es sich um den kleingeschriebenen griechischen Buchstaben [Xi].

Bei Sinussignalen nimmt er den Wert $\xi = \sqrt{2} = 1,414$ an.

Crestfaktor – Strom (Formel + Einheit)

$\xi = \frac{\hat{i}}{I_{eff}}$

Kennzahlen:

$\xi =$ Crestfaktor des Stroms

$\hat{i} =$ Scheitelwert des Stroms

$I_{eff} =$ Effektivwert des Stroms

Einheit

Dieser Faktor ist dimensionslos.

Crestfaktor – Spannung (Formel + Einheit)

$\xi = \frac{\hat{u}}{U_{eff}}$

Kennzahlen:

$\xi =$ Crestfaktor des Stroms

$\hat{i} =$ Scheitelwert der Spannung

$I_{eff} =$ Effektivwert der Spannung

Einheit

Dieser Faktor ist dimensionslos.

Wechselgrößen – Formfaktor

Als letzte Größe im Zusammenhang mit Wechselgrößen möchten wir dir nun den Formfaktor vorstellen. Dieser gibt das Verhältnis von Effektivwert zu Gleichrichtwert an. Der Wert des Faktors wird von der Kurvenform bestimmt und ist größer oder gleich 1.

Angeben wird der Formfaktor immer mit dem Formelzeichen $F$ .

Bei Sinussignalen nimmt er den Wert $F = 1,11$ an.

Formfaktor – Strom (Formel + Einheit)

$F = \frac{I_{eff}}{|\overline{i}|}$

Kennzahlen:

$F =$ Formfaktor des Stroms

$I_{eff} =$ Effektivwert des Stroms

$|\overline{i}| =$ Gleichrichtwert des Stroms

Einheit

Dieser Faktor ist dimensionslos.

Formfaktor – Strom (Formel + Einheit)

$F = \frac{U_{eff}}{|\overline{u}|}$

Kennzahlen:

$F =$ Formfaktor des Stroms

$U_{eff} =$ Effektivwert des Stroms

$|\overline{u}| =$ Gleichrichtwert des Stroms

Einheit

Dieser Faktor ist dimensionslos.

Was kommt als Nächstes?

Nachdem du jetzt die Wechselgrößen und die meisten Kennwerte der Wechselstromtechnik kennengelernt hast, stellen wir dir im nächsten Kurstext die Nullphasenwinkel vor und erklären dir was du hierzu beachten musst.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++