ET4-27 – Induktion – Bewegungsinduktion

Nachdem du bereits die Ruheinduktion als Variante der Induktion kennengelernt hast, möchten wir dir in diesem Kurstext ausführlich die Bewegungsinduktion oder anders ausgedrückt das Generatorprinzip vorstellen.

Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET5-Magnetische Felder

Merk’s dir!

“Bei der Bewegungsinduktion wird ein elektrischer Leiter durch ein Magnetfeld bewegt, dabei kommt es zu einer Spannungsinduktion in den Leiter und in den meisten Fällen daraufhin zu einem “elektrischen Stromfluss”.

Bewegungsinduktion - Generatoren — Bewegungsinduktion – Generatoren

Bewegungsinduktion – Generatorprinzip – Grundlagen

Anders als bei der Ruheinduktion wird bei der Bewegungsinduktion ein beweglicher Leiter in einem homogenen Magnetfeld bewegt. Infolge dieser Bewegung wird dem Leiter eine elektrische Spannung $U_{in} = U_q$ induziert.

Alles irgendwie anders…

Die Bewegungsinduktion findest du am ehesten in Generatoren zur Stromerzeugung (Windkrafträder) wieder. Denn hier wird eine Leiterschleife (bzw. Vielzahl von Spulen) in einem magnetischen Feld gedreht, um eine Spannung zu induzieren und damit auch einen elektrischen Strom zu erzeugen.

Es liegt das umgekehrte Wirkprinzip eines Gleichstrommotors vor.

Bewegungsinduktion - Windkraftanlage — Bewegungsinduktion – Windkraftanlage

Merk’s dir!

Hier wird mechanische Energie in elektrische Energie umgewandelt. Aus diesem Grund spricht man bei dieser Art der Induktion auch vom dem Generatorprinzip. Die dabei induzierte Spannung, also infolge der Rotation, ist eine Wechselspannung.

Bewegungsinduktion – Prinzip (Generatorprinzip)

In der nachfolgenden Abbildung siehst du das Prinzip der Bewegungsinduktion nochmals verdeutlicht. Während die magnetischen Feldlinien horizontal verlaufen, bewegt sich der im Magnetfeld befindliche Leiterteil mit der Länge $l_s$ um den Weg $x$ nach unten.

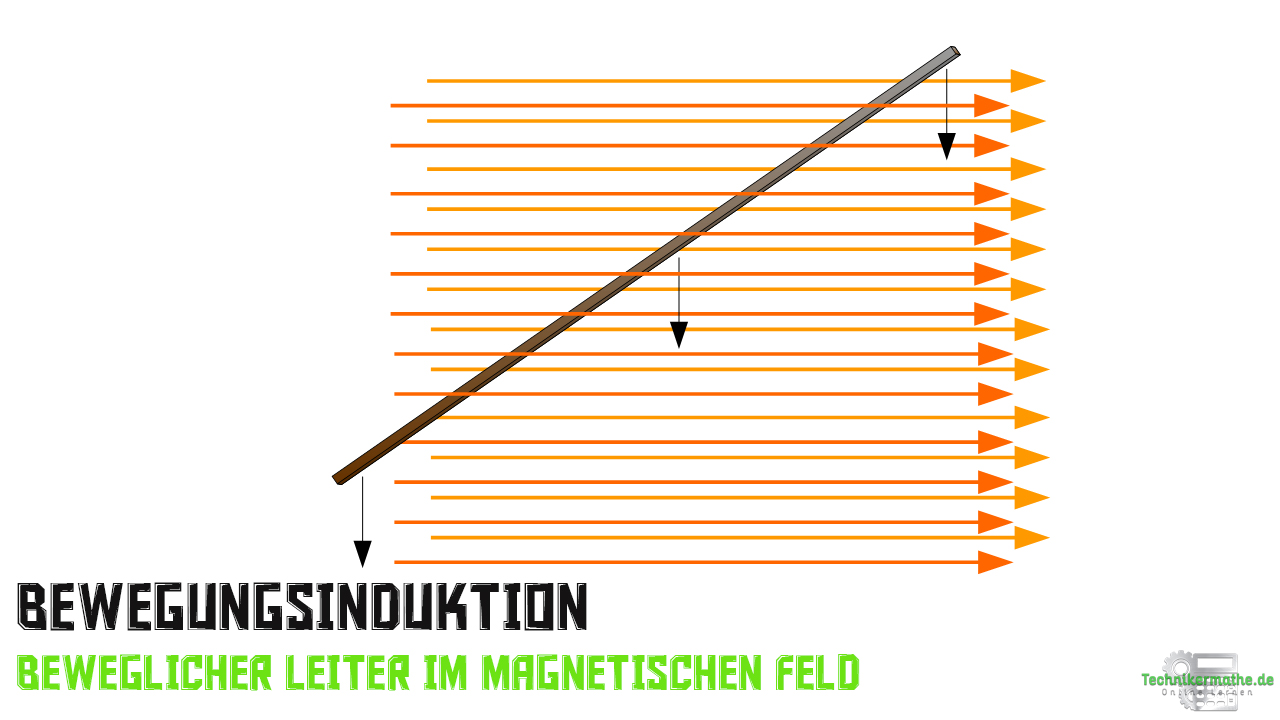
In der nächsten Abbildung siehst du Vorgang in zwei Schritten.

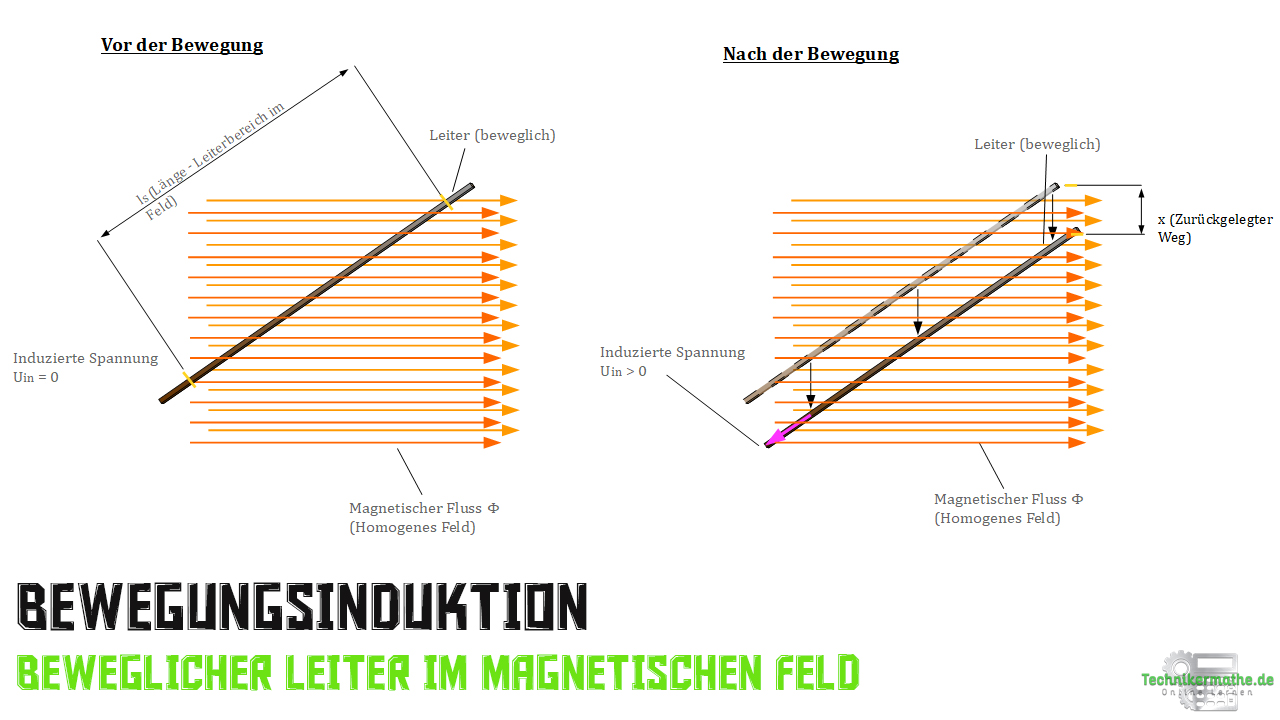
Bewegungsinduktion - Ablauf — Bewegungsinduktion – Ablauf

Bewegungsinduktion – Formeln – Berechnungen

Jetzt wollen wir die Gleichungen und Formeln näher betrachten, die es uns erlauben Aussagen bezüglich

induzierte Spannung

sowie

magnetischem Fluss

sowie

elektrischen Feldstärke

zu treffen.

Berechnung – Induzierte Spannung

Bei der Berechnung der Spannung greifen wir auf unsere bekannte Gleichung aus einem vorherigen Text zurück.

Leiterschleife, Leiter

Wird lediglich ein Leiter oder eine Leiterschleife mit lediglich einer Windung $N = 1$ in das Magnetfeld geführt, so bestimmt sich die induzierte Spannung mit:

$U_{in} = \frac{\Delta \Phi}{\Delta t}$ Leiterschleife

Kennzahlen:

$U_{in} =$ Induzierte Spannung

$\Phi =$ Magnetischer Fluss

$\frac{\Delta \Phi}{\Delta t} =$ Zeitliche Änderung des magnetischen Flusses

Spule

Wird hingegen nicht nur ein Leiter, bzw. eine Leiterschleife, sondern eine aus mehreren Leiterschleifen bestehende Spule $N > 1$ durch das homogene Magnetfeld bewegt, ergänzen wir die Gleichung um die Anzahl der Windungen $N$ .

$U_{in}= \frac{\Delta \Phi}{\Delta t} \cdot N$ Spule

Kennzahlen:

$U_{in} =$ Induzierte Spannung

$\Phi =$ Magnetischer Fluss

$\frac{\Delta \Phi}{\Delta t} =$ Zeitliche Änderung des magnetischen Flusses

$N =$ Windungszahl

Berechnung – Magnetischer Fluss

In den Gleichungen zur Berechnung der Spannungen für die Leiterschleife und der Spule ist die Zeit abhängige Veränderung des Magnetischen Flusses die zentrale Größe. Der Magnetische Fluss errechnet sich nach der bekannten Gleichung:

$\Phi = B \cdot A$

Kennzahlen:

$\Phi =$ Magnetischer Fluss

$B =$ Magnetische Flussdichte

$A =$ Fläche (aufgespannt)

Es kommt auf die Fläche an…

Entscheidend für die Berechnung des magnetischen Flusses ist nicht die magnetische Flussdichte (wie bei der Ruheinduktion), sondern die aufgespannte Fläche von Leiterbereich im Feld $l_s$ multipliziert mit dem Weg $x$ den der Leiter im Magnetfeld zurücklegt.

Formal sieht das dann so aus:

$A = l_s \cdot x$

Kennzahlen:

$A =$ Aufgespannte Fläche

$l_s =$ Leiterbereich im Feld

$x =$ Zurückgelegter Weg

Herleitung – Induzierte Spannung

Jetzt gehen wir den ganzen Weg wieder zurück.

Einsetzen der Gleichung für die Fläche A in die Gleichung für den Magnetischen Fluss

$\Phi = B \cdot A = B \cdot l_s \cdot x$

Diese Gleichung setzen wir wiederum in die Gleichung für die induzierte Spannung ein.

$U_{in} = \frac{\Delta \Phi}{\Delta t} = \frac{\Delta (B \cdot l_s \cdot x)}{ \Delta t}$

So sieht die Gleichung aber sehr unelegant aus. Daher sollten wir jetzt überlegen, welche Größe hier letztlich zeitabhängig ist. Da sich die Flussdichte und auch der Bereich des Leiters nicht verändern, ist es lediglich der Weg, der eine Zeitabhängigkeit besitzt. Oder umfassender betrachtet, es gut um die Bewegung die der Leiter absolviert – Demnach: Bewegungsinduktion.

Aus diesem Grund formulieren wir die Gleichung in der neuen Form:

$U_{in} = \frac{\Delta \Phi}{\Delta t} = B \cdot l_s \cdot \frac{\Delta x}{\Delta t}$

Bewegungsgeschwindigkeit des Leiters

Es kommt auf die Geschwindigkeit an…

Wenn du dich jetzt an den Physikunterricht erinnerst, dann sollte dir einfallen, dass die Geschwindigkeit eines Körpers immer Weg pro Zeit ist.

$\Delta x}{\Delta t} = \frac{x}{t} = v$

Kennzahlen:

$x =$ Weg

$t =$ Zeit

$v =$ Geschwindigkeit

Finale Gleichung der induzierten Spannung

Jetzt kommen wir zur finalen und angepassten Gleichung zur Bestimmung der Bewegungsinduktion im bewegten Leiter in Abhängigkeit von der Bewegungsgeschwindigkeit.

$U_{in} = B \cdot l_s \cdot v$

Kennzahlen:

$U_{in} =$ Induzierte Spannung

$B =$ Magnetische Flussdichte

$l_s =$ Leiterbereich im Feld

$v =$ Geschwindigkeit des Leiters im Feld

Bestimmung der Elektrischen Feldstärke

Wenn man jetzt noch die Elektrische Feldstärke $E$ ermitteln möchte, so kann man sich ganz einfach unserer finalen Gleichung bedienen.

Hierzu dividieren wir die Gleichung durch $l_s$ und haben dann auf der linken Seite der Gleichung stehen:

$\frac{U_{in}}{l_s} = ….$

Das Entspricht formal $E$

$\frac{U_{in}}{l_s} = E$

Die Elektrische Feldstärke lässt sich also mit dem Produkt aus magnetischer Flussdichte und der Bewegungsgeschwindigkeit des elektrischen Leiters ermitteln.

$E = B \cdot v$

Kennzahlen:

$E =$ Elektrische Feldstärke

$B =$ Magnetische Flussdichte

$v =$ Bewegungsgeschwindigkeit des Leiters im magnetischen Feld.

Was kommt als Nächstes?

Nachdem wir nun ausführlich über die Bewegungsinduktion (Generatorprinzip) und die damit verbundenen Gleichungen und Größen gesprochen haben, gehen wir im nächsten Kurstext auf der Thema Hysterese detailliert ein.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++