ET4-22 – Magnetisches Feld – Durchflutungsgesetz

In diesem Kurstext erklären wir dir ausführlich das Durchflutungsgesetz für magnetische Felder und stellen wir dabei die wichtigen Formeln zur Berechnung der Durchflutung vor.

Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET5-Magnetische Felder

Merk’s dir!

“Das Durchflutungsgesetz besagt, dass ein elektrischer Strom ein zu seiner Stärke proportionales Magnetfeld erzeugt und die Richtung des Magnetfeldes zusammen mit dem Strom eine rechtsdrehende Schraube erzeugt.”

Durchflutungsgesetz - Zusammenhang von Strömen und Magnetfeldern — Durchflutungsgesetz – Zusammenhang von Strömen und Magnetfeldern

Durchflutungsgesetz – Grundlagen

Es beschreibt, einfach gesprochen, den Zusammenhang zwischen dem Strom und der von ihm erzeugten magnetischen Feldstärke.

Moment mal, das heißt doch ganz anders…

Richtig! Das Durchflutungsgesetz hat wie viele andere Gesetze in der Elektrotechnik nicht nur einen Namen, sondern gleich mehrere. So wirst du je nach Fachliteratur auch Begriffe wie

Durchflutungssatz

sowie

Ampèresches Gesetz

finden.

Wofür braucht man das?…

Unabhängig von der Namensgebung handelt es sich um ein Gesetz aus der Elektrodynamik und gleichzeitig um eine der insgesamt vier bekannten maxwell’schen Gleichungen.

Der Entdecker und Namensgeber Andre-Marie Ampere formulierte damit ein Gesetz für den Magnetismus welches im Gegensatz zum Induktionsgesetz steht. Letzteres erklären wir dir in einem der nächsten Kurstexte. James Clerk Maxwell erkannte jedoch die Unvollständigkeit des Gesetzes und erweiterte es.

Bevor wir uns dem Durchflutungsgesetz zuwenden, überlegen wir zunächst was überhaupt mit der Durchflutung gemeint ist.

Durchflutung

“Die Summe der Ströme die einen festgelegten Bereich (Fläche) durchlaufen, nennt man Durchflutung $\eta$ .”

Wir unterscheiden bei der Durchflutung zwei Ausprägungen.

Fläche $A$ wird von verschiedenen voneinander unabhängigen Leitern durchzogen
Fläche $A$ wird von einer Spule, als ein einziger Leiter durchflossen.

Wir stellen uns im ersten Schritt eine Fläche $A$ vor, durch welche Ladungsträger fließen. Die Ladungsträger verhalten sich aber nicht homogen miteinander, sondern haben zueinander eine unterschiedliche Richtung und auch in Hinblick auf deren Intensität gleichen sich diese nicht.

Die Antriebskraft der Ladungsträger ist ein Magnetfeld.

Anderer Name gefällig?…

Im Rahmen dieses Kurses haben wir, wenn es sich um Ladungsträger gehandelt hat, immer von einem Strom gesprochen. Mit dieser „Tradition“ brechen wir an dieser Stelle und werden ab jetzt von einer Durchflutung sprechen.

Durchflutung – Formel und Berechnung mit mehreren Leitern

Das Kurzzeichen für die Durchflutung ist der griechische Buchstabe $\eta$ [Eta]. Formal bestimmt sich die Durchflutung mit dem Produkt aus Stromdichte $\vec{J}$ und Flächenintegral $\vec{A}$ :

$\eta = \int_{A} \vec{J} d \vec{A}$

Merk’s dir!

Kleiner Hinweis: Wir verwenden bei der Gleichung Vektoren, da die Stromdichten unterschiedliche Positionen und Richtungen aufweisen.

Jetzt liegen uns aber nicht nur ein elektrischer Leiter mit Ladungsträgerbewegung von, die die Fläche $A$ passieren, sondern eine Vielzahl mit unterschiedlichen Intensität und Richtung, wie in der nächsten Abbildung dargestellt.

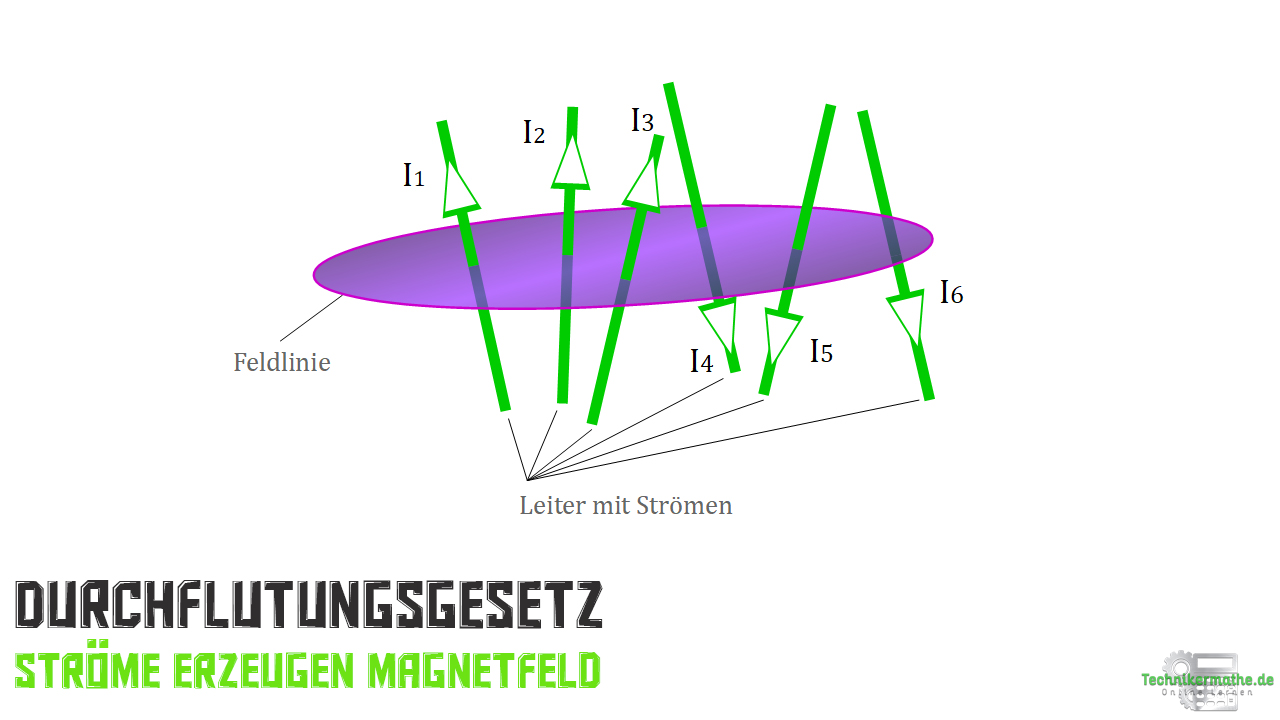
Durchflutungsgesetz , Ampere'sches Gesetz — Durchflutungsgesetz , Ampere’sches Gesetz

Nun können wir die Durchflutung der Fläche $A$ durch die Summe der einzelnen Stromstärken bestimmen. Denn es gilt ja:

$I = J \cdot A$

Formal sieht das dann so aus:

$\eta = I_1 + I_2 + I_3 + I_4 + I_5 + ….. + I_n$

Aufstellen der angepassten Gleichung

Schauen wir uns nach mal die obige Abbildung an, so fällt uns sehr schnell auf, dass einige Ströme von oben nach unten verlaufen sowie anderen Ströme die entgegengesetzte Richtung aufweisen. Dies müssen wir selbstverständlich in unserer Gleichung berücksichtigen. Angepasst steht dann da:

$\eta = - I_1 - I_2 - I_3 + I_4 + I_5$

Um die Durchflutung auf den Wert $\eta = 0$ zusetzen, so muss man die Ströme aufeinander abstimmen.

$\eta = 0 = - I_1 - I_2 - I_3 + I_4 + I_5$

Umgestellt ergibt sich ein Gleichgewicht zwischen den gleichgerichteten Strömen und denen die entgegensetzt verlaufen.

$I_1 + I_2 + I_3 = I_4 + I_5$

Sind nun alle Werte auf einer Seite gegeben, so weißt du wie die Stromdichten auf der anderen Seite der Gleichung angepasst werden müssen, damit die Durchflutung auf den Wert $\eta = 0$ fällt.

Hä??? Da fehlt doch was!…

Ist dir eigentlich aufgefallen, dass wir den Strom $I_6$ gar nicht berücksichtigt haben? – Warum auch? Dieser liegt nicht in der von uns zuvor festgelegten Fläche uns ist daher uninteressant für uns.

Durchflutung – Formel und Berechnung mit einer Spule

Liegt uns ein einzelner Leiter vor, der die Fläche $A$ mehrfach passiert, so sprechen wir von einer Spule.

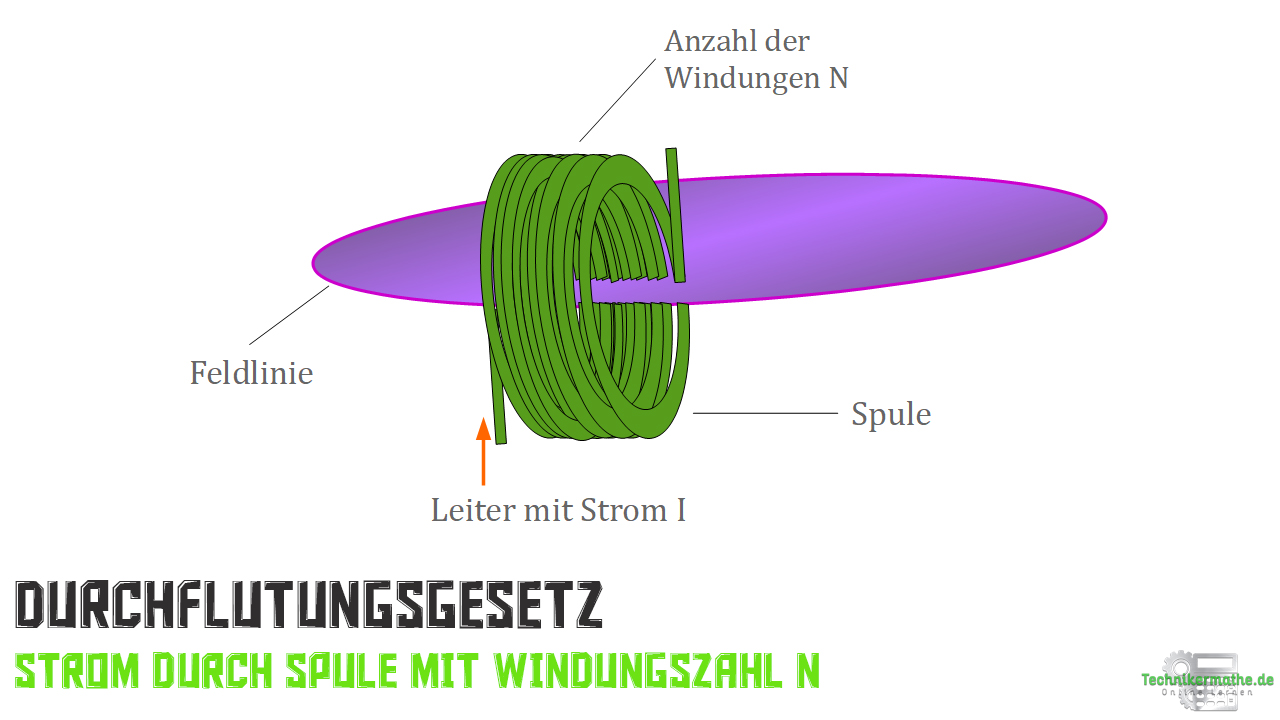
Durchflutungsgesetz - Durchflutung mit einer Spule — Durchflutungsgesetz – Durchflutung mit einer Spule

Das vereinfacht unsere Berechnung erheblich, denn nun haben wir lediglich eine Stromdichte J und somit auch nur einen Strom I. Interessant ist für uns jetzt nur noch die Windungszahl N, also die Anzahl der Kontakte zwischen Leiter und Fläche (Durchläufe):

$\eta = \int_A \vec{S} d \vec{A} = N \cdot I$

Merk’s dir!

Aufgepasst:

Die Angabe der Durchflutung erfolgt bei Spulen in der Einheit Amperewindungen. Nicht in der Einheit Ampere.

Durchflutungsgesetz – Formel und Berechnung

Das Durchflutungsgesetz beinhaltet die magnetische Feldstärke $\vec{H}$ sowie den Weg $\vec{s}$ als Größen und wird formal dargestellt mit einen Kreisintegral.

Wir wählen ein Kreisintegral da im Magnetfeld alle Feldlinien geschlossen sind. Außerdem ist es zweckmäßig, dass wir das Integral über den geschlossenen Weg einer Feldlinie bilden.

$\oint \vec{H} \cdot \vec{s} = \eta = \int_A \vec{J} d \vec{A} = I$

Merk’s dir!

Wenn du jetzt genau hinschaust, so erkennst du, dass du mit jedem Umlauf (Kreisintegral) am Ende auf der rechten Seite der Gleichung als Ergebnis die Stromstärke $I$ erhältst.

Was kommt als Nächstes?

Im kommenden Kurstext erfährst du wie sich die magnetische Feldstärke bei Leitern und Spulen berechnen lässt.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++