ET4-13 – Kondensatoren – Reihenschaltung

Nachdem du bereits viel über den Sinn und Zweck von Kondensatoren erfahren hast und weißt, wie du mit den zugehörigen Größen umzugehen hast, betrachten wir nun das Verhalten von einem Kondensatoren in Reihenschaltung. Alternativ spricht man auch von der Serienschaltung von Kondensatoren.

Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET4-Elektrische Felder

Kondensatoren in Reihenschaltung – Definition

Merk’s dir!

“Kondensatoren in Reihenschaltung bewirken eine Verringerung der Gesamtkapazität um Spannungsdurchschlägen entgegenzuwirken. Der Effekt ist der gleiche, wie als wenn man den Plattenabstand der einzelnen Kondensatoren vergrößert. Die Plattenflächen bleiben in Summe unverändert.”

Kommt mir bekannt vor…

Wir kennen das Verhalten von Ohm’schen Widerständen in Parallelschaltungen (nicht Reihenschaltungen) und werden gleich sehr schnell merken, dass sich in Reihe geschaltete Kondensatoren doch sehr ähnlich verhalten.

Kondensatoren in Reihenschaltung – Grundlegendes

Wenn eine Reihenschaltung von Kondensatoren in einem Netzwerk gegeben ist, so weist jeder Kondensator eine Einzelkapazität auf. Diese kennzeichnen wir immer mit dem Großbuchstaben C.

Sind es insgesamt 5 Kondensatoren, so haben wir mit $C_1, C_2, C_3, C_4, C_5$ genau 5 unterschiedliche Einzelkapazitäten. Diese können alle Betragsmäßig unterschiedlich sowie identisch sein.

Gemein haben Kondensatoren aber auf jeden Fall, dass durch alle Kondensatoren bei der Reihenschaltung der gleiche Strom $I$ fließt, unabhängig von der Anzahl der Kondensatoren sowie unabhängig davon ob es sich um Gleichstrom oder Wechselstrom handelt.

Kondensatoren in Reihenschaltung – Schaltplan

In der kommenden Abbildung siehst du wie eine Reihenschaltung von Kondensatoren aussieht.

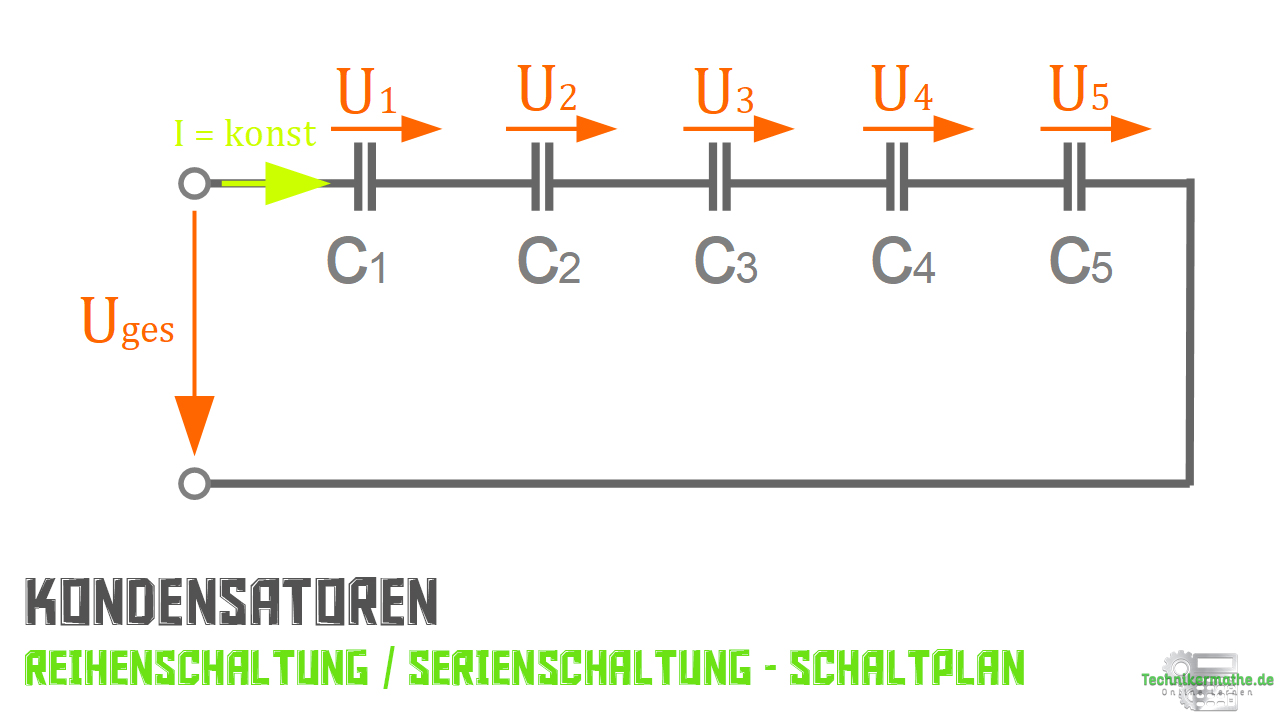
Kondensatoren in Reihenschaltung – Spannung, Ladung, Kapazität – Gleichungen + Formeln

Sind Kondensatoren in Reihe geschaltet, so sammeln sich beim Vorhandensein eines elektrischen Stroms auf allen Platten (Elektroden) die gleiche Ladung Q an.

Grundgleichung

Ausgehend von der bekannten Gleichung

$Q = U \cdot C$

Ergibt sich nach Umstellen für die Spannung folgende Gleichung

$U = \frac{Q}{C}$

Diese Gleichung verdeutlicht, dass jede Spannung an einem Kondensator von der örtlichen Kapazität C abhängt.

Gesamtspannung – Einzelspannung

Die Gesamtspannung $U_{ges}$ ergibt sich aus der Summe der Einzelspannungen:

$U_{ges} = \sum_{i=1}^{n} U_i = U_1 + U_2 + U_3 + U_4$

Gesamtladung – Einzelladung

Die Gesamtladung $Q_{ges}$ entspricht immer dem Wert der einzelnen Ladungen:

$Q_{ges} = Q_1 = Q_2 = Q_3 = Q_4 = Q_n$

Gesamtspannung mit Kapazität und Ladung

Aus diesen beiden Gleichungen und unter Hinzunahme der obigen Gleichung können wir für die Gesamtspannung $U_{ges}$ ableiten

$U_{ges} = U_1 + U_2 + U_3 + U_4 + U_5 + ….. + U_n = \frac{Q}{C_1} + \frac{Q}{C_2} + \frac{Q}{C_3} +\frac{Q}{C_4} +\frac{Q}{C_5} + ….. + \frac{Q}{C_n}$

verkürzt

$U_{ges} = \sum_{i = 1}^{n} U_i = \frac{Q}{\sum_{i = 1}^{n} C_i}$

Gesamtkapazität – Einzelkapazität

Wenn wir jetzt jeden Einzelspannungswert durch die Ladung Q dividieren, so erhalten wir einen passenderen Ausdruck der Gleichung. in dieser Gleichung zur Bestimmung der Gesamtkapazität der Kondensatoren tauchen nur noch Einzelkapazitäten auf:

$\frac{1}{C_{ges}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \frac{1}{C_4} + \frac{1}{C_5} + …. \frac{1}{C_n}$

Gesamtkapazität von zwei Kondensatoren

Liegen nur zwei Kondensatoren vor, so errechnet sich die Kapazität, ähnlich wie im gleichen Fall bei Widerständen mit

$\frac{1}{C_{ges}} = \frac{1}{C_1} + \frac{1}{C_2} = \frac{C_1 + C_2}{C_1 \cdot C_2}$

jetzt einfach noch den Kehrwert bilden:

$C_{ges} = \frac{C_1 \cdot C_2}{C_1 + C_2}$

Fazit zu Kondensatoren in Reihe

Die verbundenen Platten zweier in Reihe geschalteten Kondensatoren bilden gemeinsam ein isoliertes System, weshalb sich die Ladungsträger trennen lassen, ein Abfluss dieser aber nicht möglich ist.

Alle Kondensatoren haben die gleiche Ladung, wenn ein Gleichgewichtszustand vorliegt. Dieser wird erreicht, wenn in jedem Kondensator auf beiden Elektroden die exakt gleiche Anzahl von Ladungsträger mit jeweils unterschiedlicher Polarität vorliegen.

Kaum zu glauben…

Denn in einer Reihenschaltung von Kondensatoren ist die Gesamtkapazität immer kleiner als die kleinste Einzelkapazität. Daher muss der Kondensator mit der kleinsten Einzelkapazität auch die größte Spannung aufnehmen.

Verwendung für Kondensatoren in Reihe – [Zusatz-Infos]

Du hast bereits in einem vorherigen Kurstext von der Durchschlagfestigkeit gehört. Dieser Wert gibt uns das Maximum der Elektrischen Feldstärke an, bei welchem kein Spannungsdurchschlag auftritt. Ein Problem ist, dass diese unter Umständen geringer ausfallen kann als die Gesamtspannung. Daher setzt man die Reihenschaltung ein.

Würde man in diesem Fall auf eine Reihenschaltung verzichten, würde sich die Überschreitung durch Lichtbögen oder Funkenschläge bemerkbar machen. Am Ende führt dieser Umstand dann zu einer Beschädigung der Kondensatoren.

Es wird kritisch…

Es ist immer wichtig auf die Strom- und Spannungsbegrenzung beim Einsatz von Kondensatoren zu achten, da es ansonsten zu Schäden an den Kondensatoren und schlimmstenfalls der gesamten Anlagen kommen kann.

Und besonders wichtig: Geht ein Kondensator infolge eines Kurzschlusses kaputt, dann ist die Wirkung auf die anderen Kondensatoren umso höher. – Eine verstärkende Kettenreaktion tritt auf.

Beispiel! Selbsthilfe-Kondensatoren

Selbstheilende Kondensatoren können Durchschlägen zumindest teilweise entgegenwirken, indem ein Teil der Metallfolie in Folge der Hitze verdampft und so die Kapazität schwach reduziert.

Was kommt als Nächstes?

Nachdem wir ausführlich über das Thema Kondensator in Reihe gesprochen haben, erklären wir dir Im kommenden Kurstext ausführlich die Parallelschaltung von Kondensatoren inklusive der zugehörigen Berechnungen für Strom, Spannung sowie Kapazität.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++