ET4-12 – Kondensatoren – Dielektrikum

Im vorherigen Kurstext tauchten mit der Influenzkonstanten $\epsilon_0$ und der relativen Dielektrizitätskonstanten $\epsilon_r$ zwei noch nicht näher definierte Größen auf. Diese möchten wir dir in diesem Kurstext als Dielektrikum näher erklären.

Für ein optimales Verständnis helfen dir in diesem Kursabschnitt drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET4-Elektrische Felder

Dielektrikum - Kondensatoren — Dielektrikum – Kondensatoren

Dielektrikum – Grundlagen

Wenn wir von dem Bereich zwischen zwei Elektroden im Zusammenhang mit Elektroden sprechen, so müssen wir im ersten Schritt folgende Größen und Begriffe unterscheiden:

$\epsilon_0$ = Elektrische Feldkonstante oder Influenzkonstante

sowie

$\epsilon_r$ = Relative Permittivität oder Dielektrizitätskonstante

sowie

$\epsilon = \epsilon_0 \cdot \epsilon_r$ = Permittivität oder Dielektrizitätskonstante

Diese bauen wir in unsere Gleichung als Materialeinfluss des Nichtleiters ein. Es handelt sich aber um eine sehr kleine Größe.

Merk’s dir!

Um das Verhalten der unterschiedlichen Nichtleiter im elektrischen Feld ordentlich zu unterscheiden, bezieht man sich mit allen Werten auf den Wert von $\epsilon_0$ des leeren Raumes.

Dielektrikum – Elektrische Feldkonstante

Die elektrische Feldkonstante oder auch Influenzkonstante ist der kleinste Wert von $\epsilon$ .

Merk’s dir!

Denn im leeren Raum gibt es keine Wechselwirkungen zwischen elektrischem Feld und Molekülen.

Die elektrische Feldkonstante hat den Wert:

Elektrische Feldkonstante – Formel

$\epsilon_0 = 8,84519 \cdot 10^{-12} \frac{A \cdot s}{Vm}$

Bei allen anderen Nichtleitern gilt immer

$\epsilon = \epsilon_0 \cdot \epsilon_r$

Dielektrikum – Dielektrizitätskonstante

Die Dielektrizitätskonstante oder auch Dielektrizitätszahl (sowie relative Permittivität), ist eine Verhältniszahl.

In der nachfolgenden Liste findest du eine Auswahl von Angaben zu unterschiedlichen Nichtleiter-Materialien.

Beispiele! Nichtleiter-Materialien

Glas: $\epsilon_r = 3 -12$

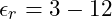
sowie

Wasser: $\epsilon_r = 80$

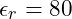
sowie

Polystyrol: $\epsilon_r = 2,3$

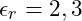
sowie

Porzellan: $\epsilon_r = 6$

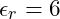
sowie

Luft: $\epsilon_r = 1,00058$

Einfluss des Dielektrikum

Um den Einfluss unterschiedlicher Dielektrika besser verstehen zu können, schauen wir uns drei herkömmliche Fälle genauer an:

1. Fall: Grenzfläche steht senkrecht zum Feldlinienverlauf

2. Fall: Grenzfläche verläuft parallel zum Feldlinienverlauf

3. Fall: Grenzfläche steht in einem freigewählten Winkel zum Feldlinienverlauf.

Und als nächstes?…

Jeden dieser Fälle betrachten wir nun im Einzelnen.

Fall 1: Grenzfläche steht senkrecht zum Feldlinienverlauf

Dabei gehen wir von einem Bereich zwischen den Elektroden (Platten) aus, der nun nicht mehr aus einem Dielektrikum besteht, sondern aus zwei unterschiedlichen Dielektrika mit ungleichen Werten. Die Fläche, die diese beiden Bereiche trennt, bezeichnet man als Äquipotentialfläche.

Merk’s dir!

Die beiden Dielektrika bilden 2 Kondensatoren, welche wir hier mit $C_1$ und $C_2$ bezeichnen.

In der nächsten Abbildung ist dieser Vorgang verbildlicht.

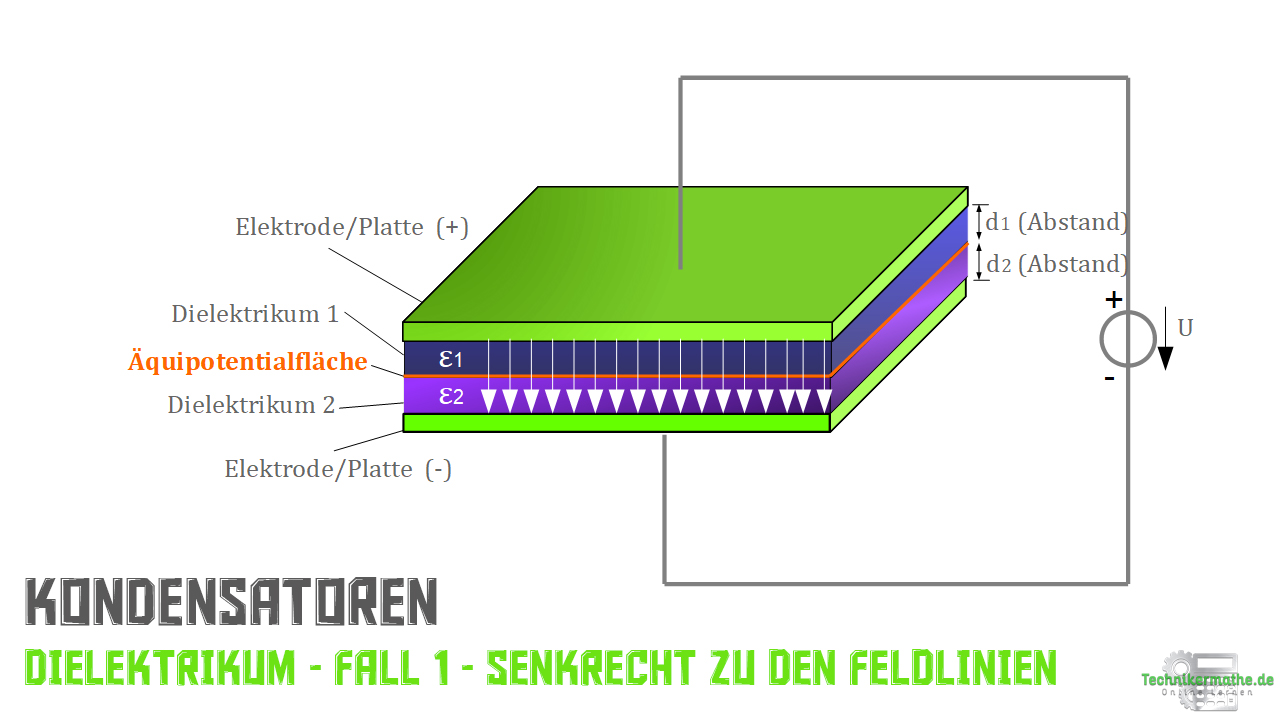
Fall 1 - Senkrecht zu den Feldlinien — Fall 1 – Senkrecht zu den Feldlinien

Merk’s dir!

In beiden Kondensatoren liegt die identische Verschiebungsdichte D vor, da die Äquipotentialfläche für beide Kondensatoren als Elektrode wirkt. Zudem gilt, dass jeder Kondensator die gleiche Ladung bei einer gleichen Fläche besitzt.

Deshalb gilt auch für beide Kondensatoren der Gleiche Wert für D:

$D = \frac{Q}{A} = \text{konstant} = \epsilon_0 \cdot \epsilon_{r_1} \cdot E_1 = \epsilon_0 \cdot \epsilon_{r_2} \cdot E_2$ Verschiebungsdichte

Jeweils nach den Feldstärken $E_1$ und $E_2$ aufgelöst bedeutet dies:

Elektrische Feldstärken – Formel

$E_1 = \frac{1}{\epsilon_0 \cdot \epsilon_{r_1}} \cdot D$ Feldstärke 1

sowie

$E_2 = \frac{1}{\epsilon_0 \cdot \epsilon_{r_2}} \cdot D$ Feldstärke 1

Vergleicht man diese beiden Gleichungen nun miteinander, so fällt uns direkt ins Auge, dass das Verhältnis der Feldstärken $E_1$ und $E_2$ umgekehrt proportional zu ihren jeweiligen Dielektrizitätszahlen verläuft. ( $D$ und $\epsilon_0$ kürzen sich heraus)

$\frac{E_1}{E_2} = \frac{\epsilon_{r2}}{\epsilon_{r1}}$ Verhältnis der Feldstärken

Fall 2: Grenzfläche verläuft parallel zum Feldlinienverlauf

“Jetzt verläuft die Grenzfläche parallel zum Feldlinienverlauf.”

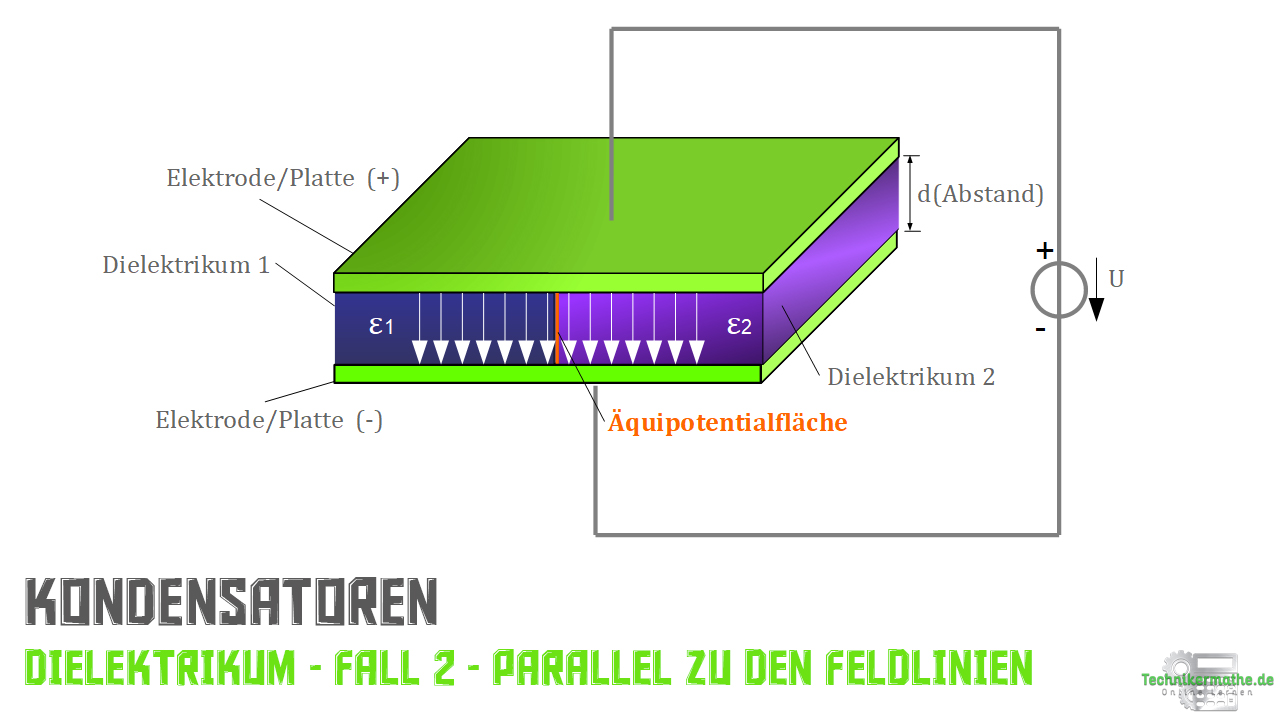
Fall 2 - Parallel zu den Feldlinien — Fall 2 – Parallel zu den Feldlinien

Merk’s dir!

Die beiden Dielektrika bilden erneut 2 Kondensatoren, welche wir hier mit $C_1$ und $C_2$ bezeichnen. Jedoch mit dem Unterschied, dass Sie nun parallel geschaltet sind.

Die Dielektrika haben die gleiche Feldstärke, besitzen jedoch unterschiedliche Verschiebungsdichten.

Für die Feldstärke gilt jeweils der gleiche Wert:

$E = \frac{U}{D}$ Feldstärke

Die Verschiebungsdichten unterscheiden sich jedoch

Elektrische Verschiebungsdichten – Formel

$D_1 = \epsilon_0 \cdot \epsilon_{r1} \cdot \frac{U}{d}$ Verschiebungsdichte 1

sowie

$D_2 = \epsilon_0 \cdot \epsilon_{r2} \cdot \frac{U}{d}$ Verschiebungsdichte 2

Diese beiden Gleichungen können wir nun in unsere Gleichung für die Gesamtladung einbauen:

Elektrische Gesamtladung – Formel

$Q = C_{ges} \cdot U$

Ausgeschrieben bedeutet das

$Q = Q_1 + Q_2 = D_1 \cdot A_1 + D_2 \cdot A_2$

Das bedeutet dann letztlich für die Kapazität:

Elektrische Kapazität – Formel

$C_{ges} = \frac{\epsilon_0}{d} \cdot (\epsilon_{r1} \cdot A_1 + \epsilon_{r2} \cdot A_2)$

sowie

$C_{ges} = C_1 + C_2$

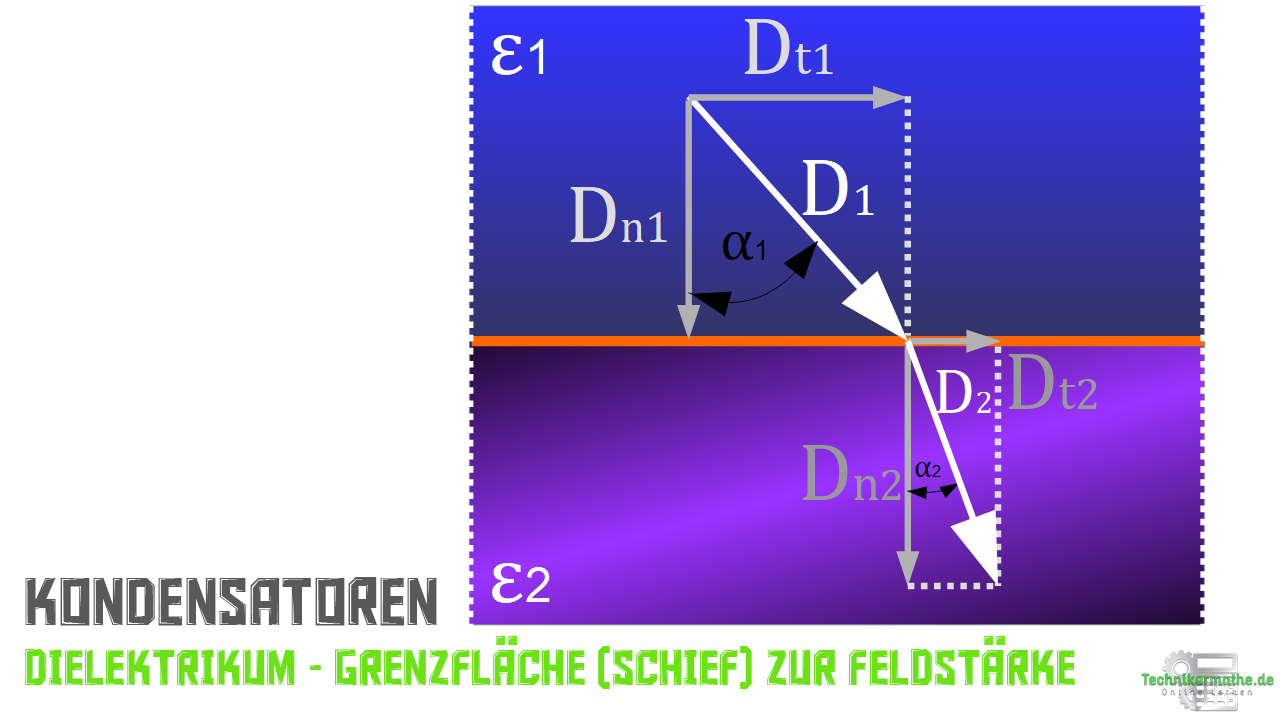
Fall 3: Grenzfläche steht in einem freigewählten Winkel zum Feldlinienverlauf

“Jetzt betrachten wir abschließend noch mal den Fall in dem die Grenzfläche zwischen den Dielektrika in einem beliebigen Winkel zum Feldlinienverlauf stehen.”

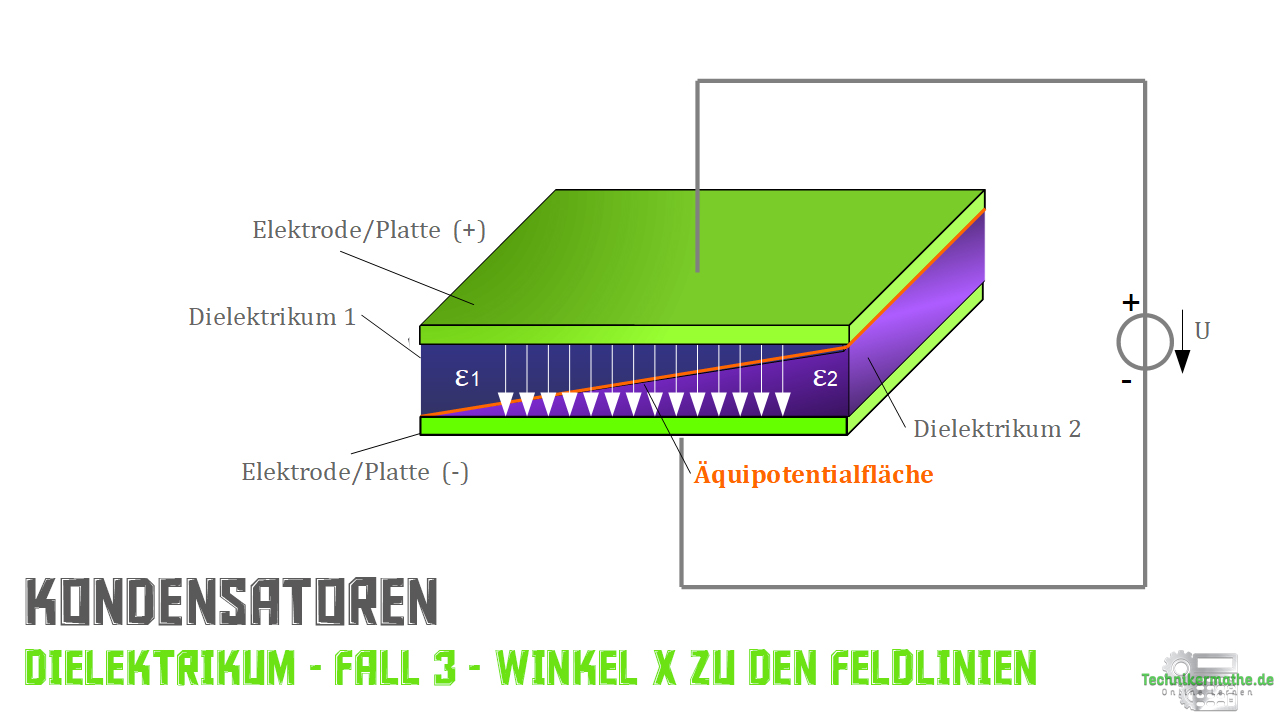
Fall 3 - Beliebiger Winkel - Dielektrikum — Fall 3 – Beliebiger Winkel – Dielektrikum

Dabei gilt:

$\epsilon_1 > \epsilon_2$

Zudem nehmen wir an, dass die Normalkomponenten der Verschiebungsdichte und die Tangentialkomponenten der Feldstärken an der Grenzfläche gleich sind. Daraus ergeben sich folgende Beziehungen:

$D_{n,1} = D_{n,2}$ Normalkomponente der Verschiebungsdichte

sowie

$E_{t,1} = E_{t,2}$ Tangentialkomponente der Verschiebungsdichte

Unter Hinzunahme der Dielektrika gelten für die Tangentialkomponenten der Verschiebungsdichte und die Normalkomponenten der Feldstärke folgende Verhältnisse:

$\frac{D_{t,1}}{D_{t,2}} = \frac{\epsilon_1}{\epsilon_2 }$ – proportionales Verhältnis

sowie

$\frac{E_{n,1}}{E_{n,2}} = \frac{\epsilon_2}{\epsilon_1}$ – umgekehrt proportionales Verhältnis

In der nächsten Abbildung siehst du, dass die Verschiebungslinien an der Grenzfläche gebrochen werden. Der Winkel in Bezug zur Grenzflächennormalen beim Übergang von einem Dielektrikum zum anderen Dielektrikum wird kleiner. Das liegt daran, dass beim oberen Dielektrikum die Dielektrizitätszahl höher ist als beim unteren Dielektrikum.

Dielektrikum - Grenzfläche schief zur Feldstärke — Dielektrikum – Grenzfläche schief zur Feldstärke

Was kommt als Nächstes?

Im nächsten Kurstext erklären wir dir wie sich Kondensatoren in der Schaltungen verhalten sowie die Berechnung der Kapazitäten. Es macht dabei Sinn, dass wir zuerst die Reihenschaltung und anschließend die Parallelschaltung behandeln.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++