ET4-11 – Kondensatoren – Kapazität

In diesem Kurstext stellen wir dir die Kapazität von Kondensatoren als Größe der Elektrotechnik im Detail vor. Hierbei betrachten wir den Fall für das homogene Feld sowie das inhomogene Feld.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET4-Elektrische Felder

Merk’s dir!

“Die Kapazität gibt das Verhältnis von elektrischer Ladung zu elektrischer Spannung an.”

Kapazität - Kondensatoren — Kapazität – Kondensatoren

Kapazität – Grundlagen

Mit der Kenntnis dieser Größe kann der Techniker eine Aussage bezüglich der gespeicherten Ladung in einem Kondensator pro elektrische Ladung angeben.

Einfach gesprochen…

Einfach gesprochen erfahren wir so wie viele Ladungsträger sich an den Elektroden ansammeln, sobald eine Spannung anliegt.

Grundgleichung und Einheit

Die Gleichung ist dann wie folgt:

$C = \frac{Q}{U}$

Die Einheit der Kapazität ist entsprechend:

$[C] = 1 F = 1 \frac{A \cdot s}{V}$ = 1 Farad

In technischen Anwendungen unterteilt man diese Grundeinheit in:

$1 F = 10^6 \mu F = 19^9 nF = 10^12 pF$

Kapazität – homogenes elektrisches Feld – Plattenkondensator

Zur Berechnung der Kapazität betrachten wir erneut eine Anordnung von zwei parallelen Platten (Elektroden), zwischen denen ein homogenes elektrisches Feld vorliegt. So wie in der nächsten Abbildung verdeutlicht.

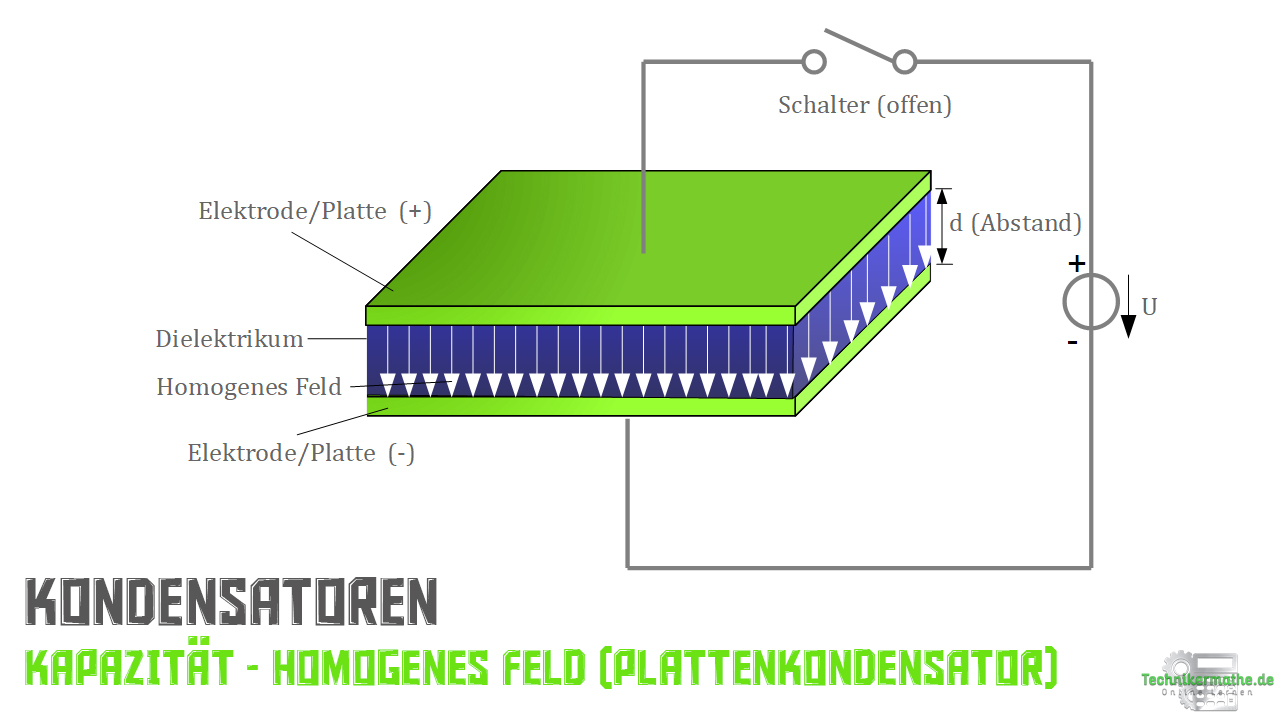
Kapazität - Homogenes Feld — Kapazität – Homogenes Feld

Hier siehst du einen Aufbau in einem Stromkreis, der einen Schalter beinhaltet. Wir sehen, dass dieser offen ist.

Wie du bereits weißt liegt zwischen diesen beiden Platten ein Dielektrikum vor.

Den Abstand der beiden Platten (Elektroden) zueinander geben wir immer mit d an und die Fläche der Platten mit einem großen A.

Der Betrag der Ladungen kann, ab dem Zeitpunkt, zu dem der Schalter geschlossen ist, gemessen werden und steht in direkter Abhängigkeit zu

der Spannung U,

sowie

der Fläche der Elektroden A,

sowie

dem Elektrodenabstand d,

sowie

der Art des Dielektrikums mit 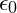$\epsilon_0$ und $\epsilon_r$ .

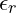Aus diesen Größen können wir nun eine Gleichung aufstellen, die wie folgt aussieht.

$Q = \epsilon \cdot \frac{A}{d} \cdot U = C \cdot U$

Das $C$ stellt die Kapazität dar. Durch Kürzen von $U$ erhalten wir eine Gleichung in der C allein auf einer Seite steht mit:

$C = \epsilon \cdot \frac{A}{d} = \epsilon_0 \epsilon_r \cdot \frac{A}{d}$

Dies ist nun die Gleichung zur Bestimmung der Kapazität eines Plattenkondensators.

Kapazität – inhomogenes Feld – Konzentrische Kugel (koaxial)

In vielen technischen Anordnung findet sich anstelle eines homogenen Feldes ein inhomogenes Feld wie bei der koaxialen Anordnung.

Kapazitäten - Koaxiale Anordnung — Kapazitäten – Koaxiale Anordnung

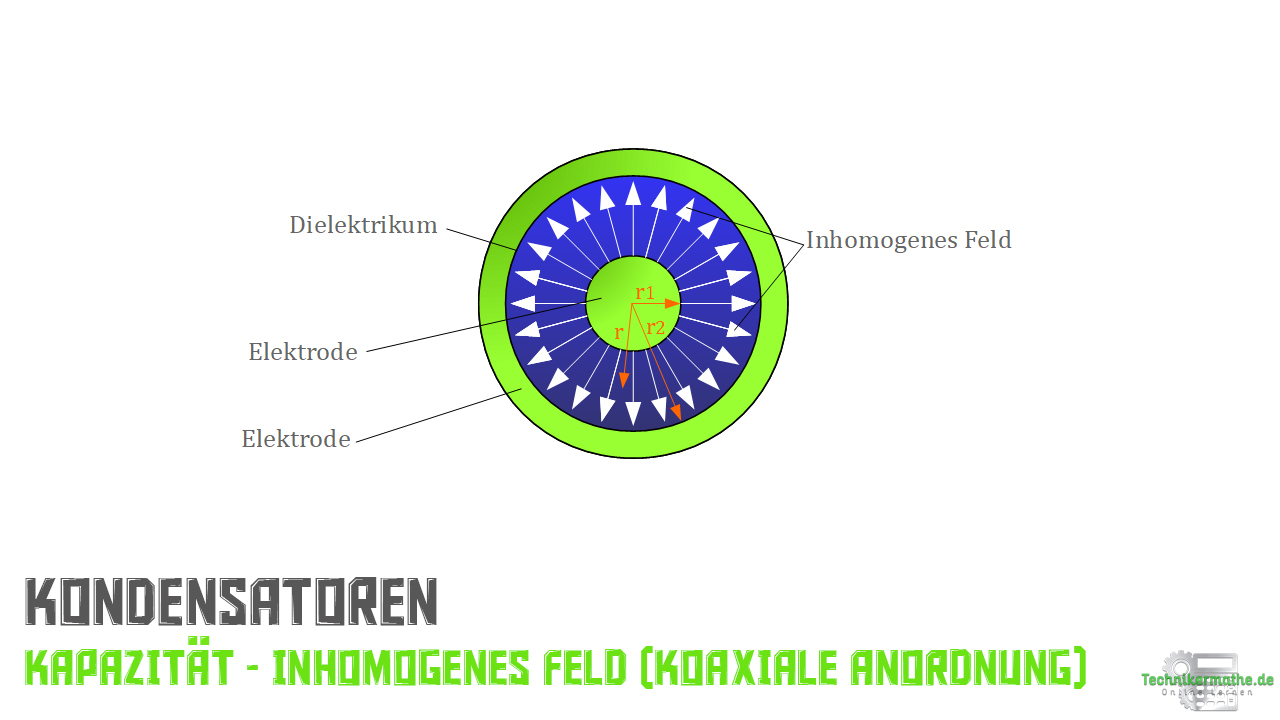
Hierzu benötigen wir eine andere Ausgangsgleichungen:

$Q = \oint_A \vec{D} \cdot d \cdot \vec{A}$

sowie

$A = 2 \cdot \pi \cdot r \cdot l$

Daraus bilden wir eine Gleichung für die elektrische Feldstärke:

$E( r ) = \frac{Q}{2\cdot \pi \cdot r \cdot l \cdot \epsilon_0 \cdot \epsilon_r }$

Zwischen den Leitern, also Hülle sowie Kern, ergibt sich eine Spannung U in Höhe von

$U = \int_{r_1}^{r_2} E( r) \cdot dr = \frac{Q}{2\cdot \pi \cdot r \cdot l \cdot \epsilon_0 \cdot \epsilon_r } \cdot ln \frac{r_2}{r_1}$

Wir wissen, dass immer noch die Beziehung

$C = \frac{Q}{U}$

gilt, erhalten wir somit für die Kapazität der Koaxialen Anordnung folgende Gleichung:

$C = \frac{2 \cdot \pi \cdot r \cdot l \cdot \epsilon_0 \cdot \epsilon_r }{ ln \frac{r_2}{r_1}}$

Für eine konzentrische Kugel gilt, dass

$C = 4 \cdot \pi \cdot \epsilon_0 \cdot \epsilon_r \cdot \frac{r_1 \cdot r_2}{r_2 - r_1}$

ist.

Messmöglichkeiten

Die Messung der Kapazität kann auf unterschiedliche Arten erfolgen. Dabei nutzen auch andere Sensoren das Prinzip der Kapazitätsmessung um beispielsweise Drücke, Feuchtigkeiten oder Gaskonzentrationen zu ermitteln.

In der Vergangenheit haben sich nachfolgende Methoden als besonders effizient erwiesen:

Laden des Kondensators mit einem konstanten elektrischen Strom und anschließender Messung der Spannungsanstiegsgeschwindigkeit.

sowie

Messen der Resonanzfrequenz von einem LC-Schwingkreis, der durch eine Kapazität gebildet wurde

sowie

Anlegen einer Wechselspannung sowie anschließendes Messen des Verlaufs des elektrischen Stroms.

Merk’s dir!

Speziell die letzte Variante gibt Rückschlüsse auf die Impedanz, den Verlustwinkel sowie den Gütefaktor des Kondensators und wird daher in Kapazitätsmessgeräten eingesetzt.

Was kommt als Nächstes?

Im kommenden Kurstext betrachten wir die Dielektrizität sowie die Dielektrizitätskonstanten im Detail, bevor wir mit der Anordnung von Kondensatoren in Reihen- und Parallelschaltungen starten.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++