(ET3-12) Netzwerkberechnung – Zweipoltheorie [Beispielaufgabe auf Klausurniveau]

Nach der ganzen Theorie folgt nun für dich eine Beispielaufgabe zur Zweipoltheorie. Diese Beispielaufgabe könnte dir in der nächsten Klausur begegnen.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET3-Netzwerkberechnung

Beispielaufgabe – Zweipoltheorie

Beispiel!

In der nächsten Abbildung ist das Netzwerk dargestellt, welches wir nun betrachten möchten. In diesem Netzwerk befinden sich insgesamt 7 Widerstände und eine Spannungsquelle. Deine Aufgabe besteht jetzt darin, die anliegende Spannung $U_4$ am Widerstand $R_4$ zu bestimmen. Die Lösung der Aufgabe erfolgt in insgesamt 8 Schritten.

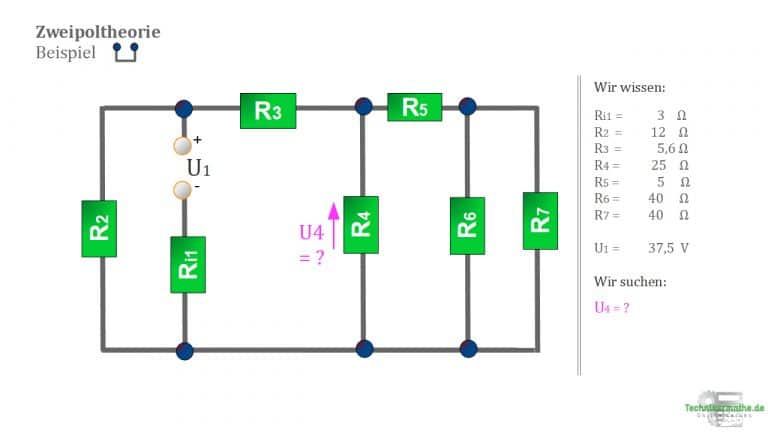
Unsere Aufgabe sei die Spannung U_4 am Widerstand R_4 zu berechnen.

Gegeben sind

Teilspannung:
$U_1 = 37,5 V$

Teilwiderstände:
$R_{i1} = 3 \Omega$

sowie

$R_{2} = 12 \Omega$

sowie

$R_{3} = 5,6 \Omega$

sowie

$R_{4} = 25 \Omega$

sowie

$R_{5} = 5 \Omega$

sowie

$R_{6} = 40 \Omega$

sowie

$R_{7} = 40 \Omega$

Lösung der Aufgabe – Zweipoltheorie

1. Lesen der Aufgabenstellung (Vorarbeit)
Deine Aufgabe besteht darin, dass du nun die Spannung $UI_4$ berechnen musst.

2. Sichten der Skizze (Vorarbeit)
Es ist immer sinnvoll, dass du der notwendigen Größe in der Abbildung kennzeichnest. Hast du dies gemacht, kannst du mit der Berechnung starten.

Beispielaufgabe - Zweipoltheorie — Beispielaufgabe – Zweipoltheorie

3. Auftrennen der Schaltung
Wie in der nächsten Abbildung sichtbar, solltest du die Schaltung auftrennen. Denn dieses Vorgehen vereinfacht unsere Berechnung.

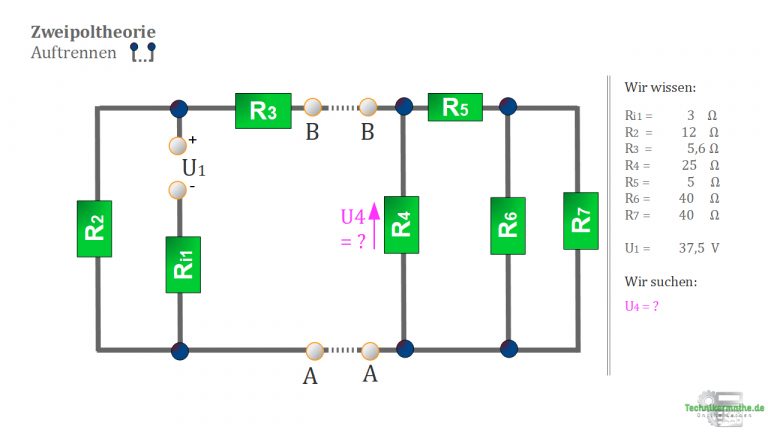
Zweipoltheorie - Auftrennen der Schaltung — Zweipoltheorie – Auftrennen der Schaltung

4. Zweipole festlegen
4.1 Jetzt führen wir den aktiven Zweipol auf eine Spannungsquellenersatzschaltung zurück. Darin befinden sich $U_1$ und $R_{i ers}$

4.2 Den passiven Zweipol hingegen führen wir auf den Ersatzwiderstand $R_a$ zurück.

4.3 Aus 4.1 und 4.2 entwickeln wir nun eine weitere Ersatzschaltung wie nachfolgend dargestellt:

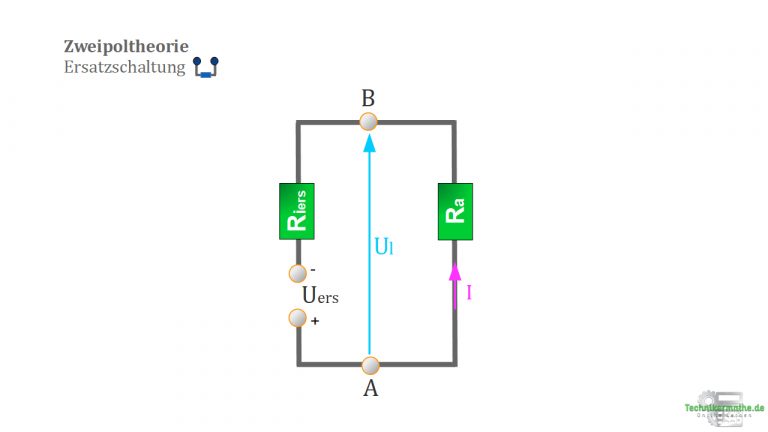
Zweipoltheorie - Ersatzschaltung — Zweipoltheorie – Ersatzschaltung

5. Berechnung des Ersatzwiderstandes $R_a$ :

$R_a = R_4 || (R_5 + R_6 || R7)$

$R_a = 25 \Omega|| (5 \Omega + 40 \Omega || 40 \Omega)$

somit ist

$R_a = 25 \Omega || (5 \Omega + 20 \Omega)$

$R_a = 12,5 \Omega$

6. Berechnung des Ersatzinnenwiderstandes $R_{i ers} }$ :

$R_{i ers} = R_3 + R_{i1} || R_2$

$= (5,6 \Omega \cdot \frac{3 \Omega \cdot 12 \Omega}{3 \Omega + 12 \Omega})$

Somit ist

$R_{i ers} = 8 \Omega$

Berechnung der Spannung

7. Berechnung der Spannung $U_4$ (Variante 1)

7.1 Hier nutzt du die Spannungsteilerregel

Der Teilwiderstand $R_3$ ist stromlos und $U_1$ liegt zwischen den Knotenpunkten $A'$ und $B'$ .

Zudem gilt, dass du aufgrund des letzten Punktes $R_3$ nicht in der Berechnung berücksichtigen musst.

$U_1 = U_1 \cdot \frac{R_2}{R_{i1} + R_2} = 37,5 V \cdot \frac{12}{3 + 12} = 37,5 V \cdot \frac{12}{15} = 30 V$

7.2 Berechnung des Stroms $I$ :

Gehen wir von der letzten Gleichung aus, dann solltest du diese einfach nach $I$ auflösen.

$I = \frac{U_1}{R_{i ers} + R_a} = \frac{30 V}{20,5 \Omega} = 1,46 A$

7.3 Berechnung der gesuchten Größe (Spannung $U_4$ )

$U_4 = I \cdot R_4 = 1,46 A \cdot 12,5 \Omega = 18,25 V}$

Alternativ kannst du $U_4$ auch über die Spannungsteilerregel bestimmen, die Gleichung ist dir ja bekannt:

$U_4 = U_1 \cdot \frac{ R_a}{R_a + R_{i ers}}$

$= 30 V \cdot \frac{12, 5 \Omega}{20,5 \Omega} = 18,25 V$

8. Formuliere den Antwortsatz:

Somit hat die gesuchte Spannung einen Wert von $U_4 = 18,25 V$

Was kommt als Nächstes?

Nachdem du jetzt ein Beispiel zur Zweipoltheorie kennengelernt hast und nun auch weißt welche Größen sich hier berechnen lassen, starten wir im kommenden Kurstext mit dem neuen Thema Strommesser. Dabei thematisieren wir die direkte und indirekte Strommessung.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++