(ET3-11) Netzwerkberechnung – Zweipoltheorie – Erklärung – Einfach gut erklärt

In diesem Kurstext erklären wir die ausführlich was die Zweipoltheorie ist und verschaffen wir einen Überblick zu aktiven und passiven Zweipolen.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET3-Netzwerkberechnung

Zweipoltheorie – Überblick

Im Rahmen der Zweipoltheorie zerlegen wir für die Berechnung von einem Netzwerk, letzteres in einen aktiven und einen passiven Zweipol.

Dadurch erhalten wir eine Ersatzschaltung, die einem Grundstromkreis sehr ähnlich und somit leicht zu berechnen ist.

Zweipoltheorie – Anwendungsbereiche

Anwendbar ist die Zweipoltheorie für Netzwerke in denen sich ausschließlich Schaltelemente mit linearer Kennlinie befinden.

Zweipoltheorie – Aktive Pole – Auswahl

Die aktiven Zweipole können mit folgenden Verfahren berechnet werden:

1. Kirchhoff’sche Sätze
2. Überlagerungssatz
3. Maschenstromverfahren
4. Knotenspannungsverfahren

Zweipoltheorie – Passive Pole – Auswahl

Die passiven Zweipole errechnen sich mit nachfolgenden Verfahren:

1. Spannungsteilerverfahren
2. Stromteilerverfahren
3. Brückenschaltung
4. Stern-Dreieck-Transformation
5. Dreieck-Stern-Transformation

Zweipoltheorie – Lösungsweg – Lösungsverfahren

Insgesamt kann du dich als Techniker an dem nachfolgenden Lösungsverfahren orientieren:

1. Trenne das Netzwerk an den Stellen der gesuchten Größe so auf, dass ein aktiver und ein passiver Zweipol vorliegt. → Nicht selten ist der passive Pol ein Widerstand, der der unbekannten Größe entspricht.

2. Berechne den Ersatzwiderstand $R_a$ des passive Pol

3. Berechne den Ersatzinnenwiderstand $R_{i ers}$ des aktiven Pol

→ ersetze hierzu alle Quellenspannungen durch Kurzschlüsse und alle Einströmungen durch Unterbrechungen.

sowie

→ Berechne den Gesamtwiderstand der verbliebenen Schaltung.

4.1. Wählst du Spannungsquellenersatzschaltung aus, so musst du die Leerlaufspannung $U_1$ aus.
Dafür stehen dir die Kirchhoff’schen Sätze, der Überlagerungssatz, der Maschenstromsatz, der Knotenpunktsatz und die Strom- und Spannungsteilerregel zur Verfügung.

Um die gesuchte Größe zu bestimmen, nutzt du folgende, dir bereits bekannte, Gleichung:

$U_1}{R_a + R_{i ers}}$

5.1 Wählst du die Stromquellenersatzschaltung aus, so musst du den Kurzschlussstrom $I_K$ bestimmen.

Um diese gesuchte Größe zu bestimmen, kannst du die nächste, dir auch bekannte, Gleichung benutzen:

$I = I_K \cdot \frac{R_{i ers}}{R_a + R_{i_ers}}$

Übungsbeispiel: Berechnung eines Stroms

Beispiel!

Genug trockene Theorie! Jetzt möchten wir unser Wissen zu dem Berechnungsverfahren am nachfolgenden Netzwerk überprüfen:

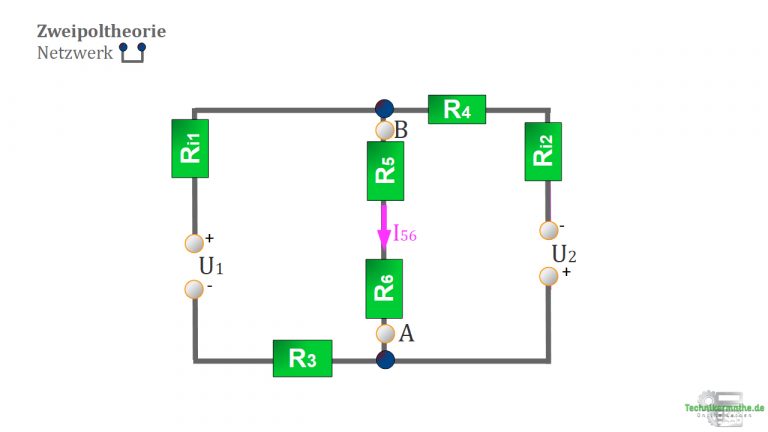
Zweipoltheorie - Netzwerk — Zweipoltheorie – Netzwerk

Unsere Aufgabe besteht darin, den Strom durch die Widerstände $R_5 R,$ $R_6$ zu bestimmen. Bei $R_6$ liegt der Strom $I_{56}$ vor.

Lösungsweg

1. Auftrennen des Netzwerks
Das Netzwerk trennen wir an den Stellen mit A und B auf. In der nächsten Abbildung hat diese Auftrennung bereits stattgefunden:

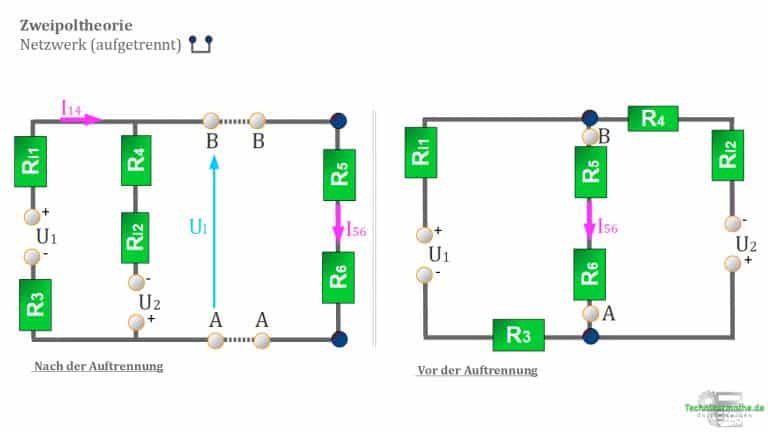
Zweipoltheorie - Auftrennung — Zweipoltheorie – Auftrennung

Links entdeckst du den aktiven Zweipol und rechts den passiven Pol.
Jetzt entspricht der Strom durch den passiven Pol dem gesuchten Strom $I_{56}$ .

2. Ersatzwiderstand des passiven Zweipols

Der Ersatzwiderstand des passiven Zweipols errechnet sich aus

$R_a = R_5 + R_6$

3. Ersatzinnenwiderstand des aktiven Zweipols
Der Ersatzwiderstand des aktiven Zweipols errechnet sich aus

$R_{i ers} = (R_{i1} + R_3) || (R_{i2} + R_4)$

Ab hier betrachten wir zwei mögliche Varianten:

Variante 1 – Benutzung der Spannungsquellenersatzschaltung:

4. Anwendung der Kirchhoff’schen Gesetze
Liegt uns eine Spannungsquellenersatzschaltung vor, so können wir die Spannung $U_1$ mit den Kirchhoff’schen Gesetzen ermitteln.

Dazu betrachten wir den Zweig auf dem sich $R_4$ und $R_{i2}$ wie im nächsten Bild dargestellt.

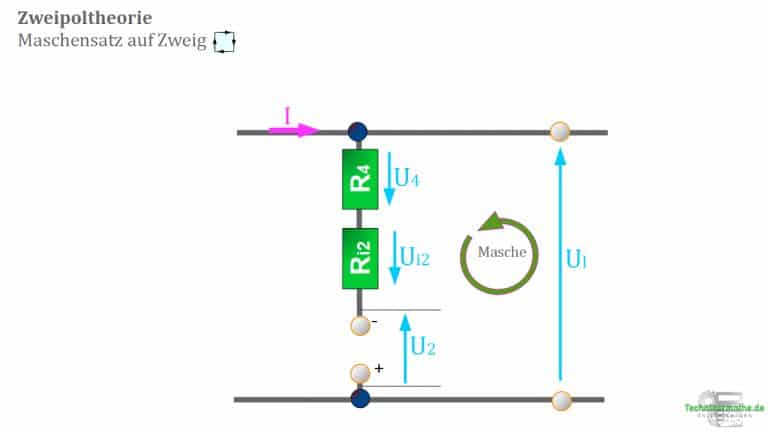
Zweipoltheorie - Maschensatz auf Zweig — Zweipoltheorie – Maschensatz auf Zweig

Auf Grundlage dieser Grafik wenden wir die Maschengleichung um $U_1$ zu ermitteln:

$U_1 + U_4 + U_{i2} - U_2 = 0$

nach $U_1$ auflösen:

$U_1 = U_2 - U_{i2} - U_4$

sowie

$U_1 = U_2 - I \cdot (R_{i2} + R_4)$

5. Ermittlung des Stroms

Bei der gegebenen Schaltung kann der Strom nur in der Masche mit den Widerständen $R_{i1}$ , $R_3$ , $R_{i2}$ und $R_{4}$ fließen.

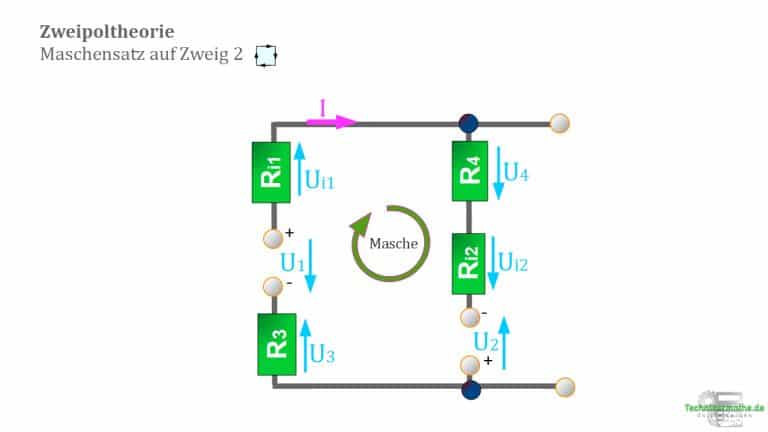
Dazu stellen wir eine passende Maschengleichung auf:

$U_{i1} + U_4 + U_{i2} - U_2 + U_3 - U_1 = 0$

sowie

$I (R_{i1} + R_4 + R_{i2} + R_3) = U_1 + U_2$

sowie

$I = \frac{U_1 + U_2}{R_{i1} + R_{i2} + R_3 + R-4}$

Somit wird $U_1$ bestimmt und anschließend können, den Strom I_{56} nach folgender Gleichung errechnen:

$I_{56} = \frac{U_1}{R_{i ers} + R_a}$

Variante 2 – Benutzung der Stromquellenersatzschaltung:

4. Anwendung des Überlagungssatzes
Liegt uns die Stromquellenersatzschaltung vor, so können wir $I_K$ nach dem Überlagerungssatz ermitteln.

Hierzu schließen wir den aktiven Pol kurz, so wie in der Abbildung dargestellt:

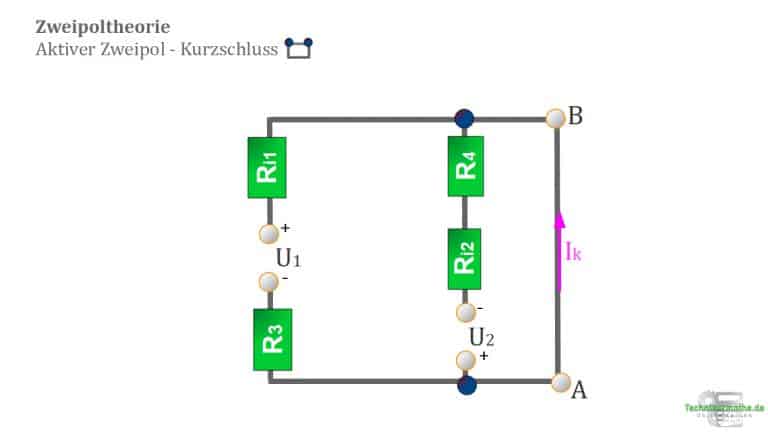
Aktiver Zweipol - Kurzschluss — Aktiver Zweipol – Kurzschluss

$I_K = I_{K2} - I_{K1}$

mit

$I_{K1} = \frac{U_1}{R_{i1} + R_3}$

sowie

$I_{K2} = \frac{U_2}{R_{i2} + R_4}$

5. Ermittlung des Stroms

Unter Benutzung der Gleichung:

$I = \frac{U_1}{R_a + R_{i ers}}$

erhalten wir für $I_{56}$

$I_{56} = I_K \frac{R_{i ers}}{R_{i ers} + R_a}$

Was kommt als Nächstes?

Damit du auch sicher bei der Anwendung dieser Rechenweise wirst, folgt im nächsten Kurstext ein ausführliches Beispiel mit Zahlenwerten.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++