(ET3-07) Knotenspannungsverfahren – Beispiel auf Klausurniveau [Musterlösung]

Damit du später als Techniker auch das Verfahren mit Knotenspannungen ganz einfach verstehst, folgt nun für dich ein ausführliches Übungsbeispiel zu diesem Thema.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET3-Netzwerkberechnung

Beispiel: Knotenspannungen – Lösen mit dem Gaußschen Algorithmus

Aufgabenstellung: Knotenspannungen

Im nächsten Bild siehst du ein Netzwerk.

Darin sind unterschiedliche Quellenspannungen $U_1, U_2, U_3$ sowie mehrere Widerstände $R_{i1}, R_{i2}, R_{i3}, R_4, R_5, R_6$ und Ströme $I_1, I_2, I_3, I_4, I_5, I_6, I_7, I_8, I_9$ eingezeichnet.

Zudem befinden sich in der Abbildung die Knotenpunkte A, B, C.

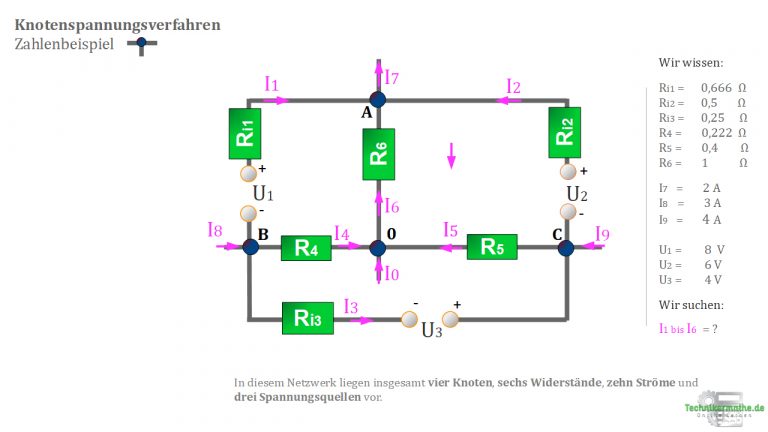
Knotenspannungen, Knotenspannungsverfahren - Zahlenbeispiel — Knotenspannungen, Knotenspannungsverfahren – Zahlenbeispiel

Die vorgegebenen Werte sind:

$U_1 = 8 V$

sowie

$U_2 = 6 V$

sowie

$U_3 = 4 V$

außerdem

$R_{i1} = 0,666 \Omega$

sowie

$R_{i2} = 0,5 \Omega$

sowie

$R_{i3} = 0,25 \Omega$

sowie

$R_4 = 0,222 \Omega$

sowie

$R_5 = 0,4 \Omega$

und

$R_6 = 1 \Omega$

Hinzukommen

$I_7 = 2 A$

sowie

$I_8 = 3 A$

und

$I_9 = 4 A$

Deine Aufgabe besteht nun darin alle unbekannten Ströme des Netzwerks mit dem Knotenspannungsverfahren zu lösen.

Merk’s dir!

Der einfachste Weg wird für dich die Verwendung des Gaußschen Algorithmus sein.

1. Berechnung der Leitwerte – Knotenspannungen

Im ersten Schritt bestimmen wir die einzelnen Leitwerte für diese Netzwerk.

1.1

$G_{i1} = \frac{1}{R_{i1}} = \frac{1}{0,666 \Omega} = 1,5 S$

|| S ist die Einheit für den Leitwert – $1 S = \text{1 Siemens} = \frac{1}{\Omega}$

1.2

$G_{i2} = \frac{1}{R_{i2}} = \frac{1}{0,5 \Omega} = 2 S$

sowie

1.3

$G_{i3} = \frac{1}{R_{i3}} = \frac{1}{0,25 \Omega} = 4 S$

sowie

1.4

$G_{4} = \frac{1}{R_{4}} = \frac{1}{0,222 \Omega} = 4,5 S$

sowie

1.5

$G_{5} = \frac{1}{R_{5}} = \frac{1}{0,4 \Omega} = 2,5 S$

sowie

1.6

$G_{6} = \frac{1}{R_{6}} = \frac{1}{1 \Omega} = 1 S$

2. Aufstellen der Knotenpunktgleichungen – Knotenspannungen

Im zweiten Schritt stellen wir die drei Knotenpunktgleichungen für die Punkte A,B,C auf.

2.1

$A: 0 = - I_7 + I_1 + I_2 + I_6$

sowie

2.2

$B: 0 = + I_8 - I_1 - I_3 - I_4$

sowie

2.3

$C: 0 = + I_9 - I_2 + I_3 - I_5$

3. Aufstellen der Zweigstromgleichungen:

Jetzt stellen wir die 6 Zweigstromgleichungen $I_1 - I_6$ auf.

3.1

$I_1 = G_{i1} \cdot (\varphi_B - \varphi_A + U_1)$

sowie

3.2

$I_2 = G_{i2} \cdot (\varphi_C - \varphi_A + U_2)$

sowie

3.3

$I_3 = G_{i3} \cdot (\varphi_B - \varphi_C + U_3)$

sowie

3.4

$I_4 = G_{4} \cdot (\varphi_B - 0) = G_{4} \cdot \varphi_B$

sowie

3.5

$I_5 = G_{5} \cdot (\varphi_C - 0) = G_{5} \cdot \varphi_C$

sowie

3.6

$I_6 = G_{6} \cdot (0 - \varphi_A) = - G_{6} \cdot \varphi_A$

4. Einsetzen in die Knotenpunktgleichungen

In diesem Schritt musst du die Zweigstromgleichungen in die Knotenpunktgleichungen einsetzen:

4.1 Einsetzen von 3.1, 3.2 und 3.6 in 2.1:

$0 = 0 = - I_7 + G_{i1} \cdot (\varphi_B - \varphi_A + U_1) + G_{i2} \cdot (\varphi_C - \varphi_A + U_2) - G_{6} \cdot \varphi_A$

sowie

4.2 Einsetzen von 3.1, 3.3 und 3.4 in 2.2:

$0 = + I_8 - G_{i1} \cdot (\varphi_B - \varphi_A + U_1) - G_{i3} \cdot (\varphi_B - \varphi_C + U_3) - G_{4} \cdot \varphi_B }$

sowie

4.3 Einsetzen von 3.1, 3.2 und 3.6 in 2.1:

$0 = + I_9 - G_{i2} \cdot (\varphi_C - \varphi_A + U_2) + G_{i3} \cdot (\varphi_B - \varphi_C + U_3) - G_{5} \cdot \varphi_C$

5. „Aufräumen“ der Knotenpunktgleichungen 4.1, 4.2 & 4.3:

Nun musst du das Gleichungssystem nach Knotenpotentialen ordnen und die zufließenden Ströme und bekannte Quellenspannungen auf eine Seite der Gleichung überführen. Für letzteres wählen wir einfach die linke Gleichungsseite.

5.1 Anpassen von 4.1:

$I_7 - G_{i1} \cdot U_1 - G_{i2} \cdot U_2 = \varphi_A \cdot (- G_{i1} - G_{i2} - G_6) + \varphi_B \cdot (G_{i1}) + \varphi_C \cdot (G_{i2})$

sowie

5.2 Anpassen von 4.2:

$- I_8 + G_{i1} \cdot U_1 - G_{i3} \cdot U_3= \varphi_A \cdot (G_{i1}) - \varphi_B \cdot (G_{i1} + G_{i3} + G_4) + \varphi_C \cdot (G_{i3})$

sowie

5.3 Anpassen von 4.3:
$- I_9 - G_{i2} \cdot U_2 - G_{i3} \cdot U_3 = \varphi_A \cdot ( G_{i2}) + \varphi_B \cdot (G_{i3}) - \varphi_C \cdot (G_{i2} + G_{i3} + G_5)$

6. Einsetzen der bekannten Zahlenwerte für die Spannungen (in V), Ströme (in $A = V \cdot S$ ) und Leitwerte (in S)

6.1 Anpassen von 5.1:

$2 A - 12 VS - 12 VS = 2 A - 12 A - 12 A = \varphi_A \cdot (4,5 S) + \varphi_B \cdot (1,5 S) + \varphi_C \cdot (2 S)$

sowie

6.2 Anpassen von 5.2:

$- 3 A + + 12 VS + 16 VS = 2 A - 12 A - 12 A = \varphi_A \cdot (1,5 S) - \varphi_B \cdot (10 S) + \varphi_C \cdot (4 S)$

sowie

6.3 Anpassen von 5.3:
$- 4 A - 12 VS - 16 VS = - 4 A - 12 A - 16 A = \varphi_A \cdot (- 2) + \varphi_B \cdot 4 - \varphi_C \cdot (8,5)$

7. Zusammenfassen der gleichen Größen – Knotenspannungen

7.1 Zusammenfassen von 6.1:
$4,5 S \cdot \varphi_A - 1,5 S \cdot \varphi B - 2 S \cdot \varphi C = + 22 A$

sowie

7.2 Zusammenfassen von 6.2:
$1,5 S \cdot \varphi_A - 10 S \cdot \varphi B + 4 S \cdot \varphi C = + 25 A$

sowie

7.3 Zusammenfassen von 6.3:
$2 S \cdot \varphi_A - 4 S \cdot \varphi B - 8,5 S \cdot \varphi C = + 22 A$

8. Anwendung des Gaußschen Algorithmus – Knotenspannungen

8.1 Wir erstellen wieder eine Matrix; Alle Werte unterhalb der Matrix müssen nun mit Hilfe der elementaren Umformungen zu Nullen überführt werden.

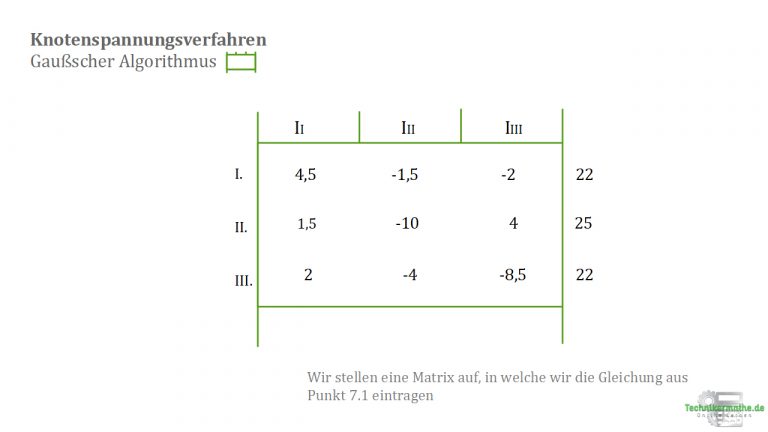
Knotenspannungen - Gauß'scher Algorithmus — Knotenspannungen – Gauß’scher Algorithmus

Ausgehend von unserer bisherigen Vorgehensweise passen wir ganz easy die Matrix an:

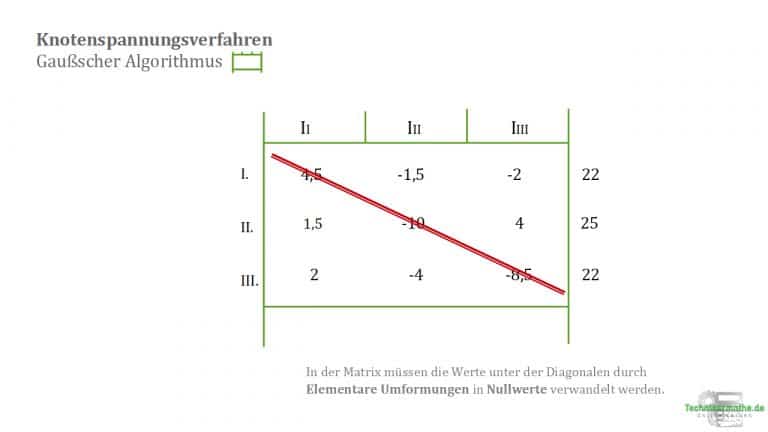
8.2 Wir beginnen mit dem ersten Wert aus der II. Indem wir die II.-Zeile mit 3 multiplizieren und anschließend I. abziehen wird $1,5 \varphi_A$ zu 0

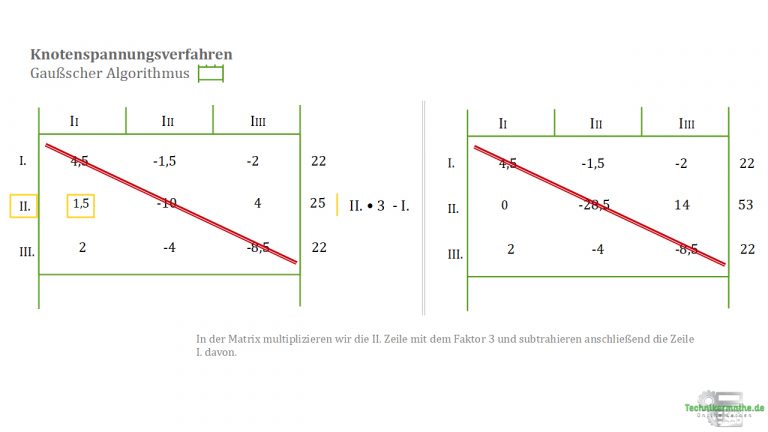
8.3 Den ersten Wert aus III eliminieren wir als Nächstes. Dazu multiplizieren wir III. mit 2,25 und subtrahieren anschließend von I. Somit wird $2 \varphi_A$ zu 0.

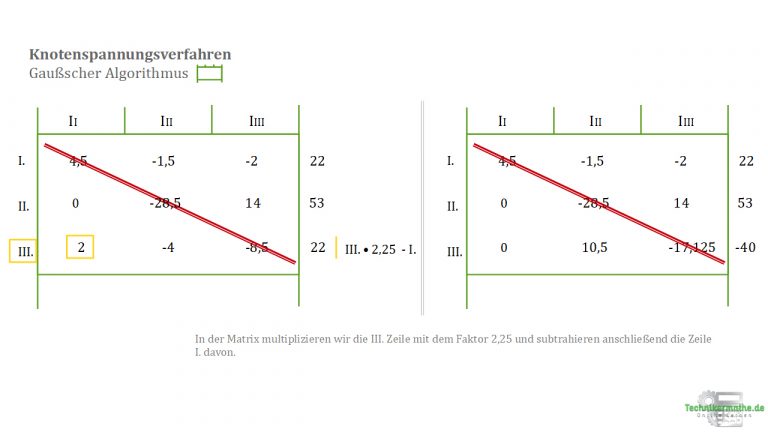
8.4 Nun nehmen wir die beiden neuen Gleichungen aus II. und III. Die Gleichung aus Zeile III. multiplizieren wir mit $\frac{19}{7}$ . und addieren diese mit Gleichung II.

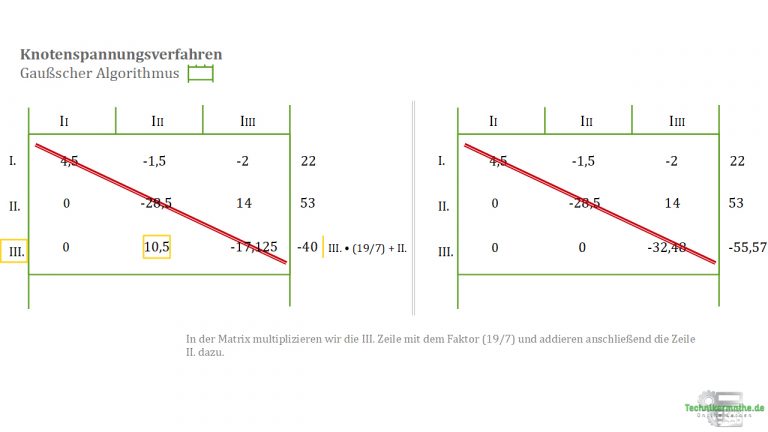
8.5 Jetzt haben wir alle Werte unterhalb der Diagonalen eliminiert und können nach $\varphi_C$ auflösen:

$\varphi_C = 1,71 V$

8.6 Den Wert für $\varphi_C$ setzen wir nun wiederum in die Gleichung II (neu) ein und lösen anschließend nach $\varphi_B$ auf.

$9,5 \varphi_B - 4,66 \cdot 1,71 = -17,66$

$\varphi_B = - 1,26 V$

8.7 Zu guter Letzt bestimmen wir nun noch $\varphi_A$ indem wir die Ergebnisse aus 8.5 und 8.6 in die Gleichung I einsetzen.

$4,5 \varphi_A - 1.5 \cdot (-1,26) - 2 \cdot (1,71) = 22$

$\varphi_A = 5,23 V$

9. Bestimmen der einzelnen Ströme!

Im allerletzten Schritt bestimmen wir die einzelnen Ströme indem wir unsere errechneten und die vorgegebenen Werte einfach in die Zweigstromgleichungen einsetzen. Zur Vereinfachung runden wir $\varphi_A = 5,23 V$ auf $\varphi_A = 5,30 V$ auf.

9.1

$I_1 = 1,5 S \cdot (-1 V - 5,3 V + 8 V) = 2,55 A$

sowie

9.2

$I_2 = 2 S \cdot (1,75 V - 5,3 V + 6 V) = 4,9 A$

sowie

9.3

$I_3 = 4 S \cdot (-1 V - 1,75 V + 4 V) = 5 A$

sowie

9.4

$I_4 = 4,5 S \cdot (-1 V) = -4,5 A$

sowie

9.5

$I_5 = 2,5 S \cdot (1,75) = 4,38 A$

sowie

9.6

$I_6 = - 1 S \cdot (5,3 V) = -5,3 A$

Merk’s dir!

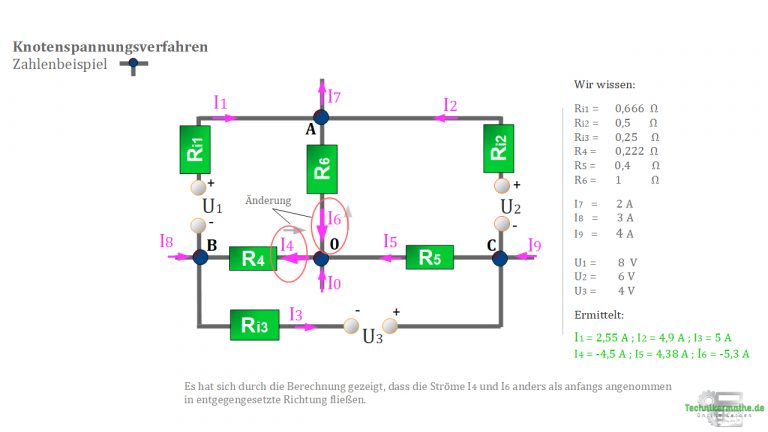
Es fällt dir vielleicht auf, dass 9,4 und 9.6 im Gegensatz zu den anderen Werten negativ ist. Keine Panik!

Das bedeutet einfach nur, dass die Ströme in die entgegensetzte Richtung fließen als wie in der Zeichnung angenommen.

10. Anpassung der Anfangszeichnung aufgrund der ermittelten Werte.

Knotenspannungen - Knotenspannungsverfahren — Knotenspannungen – Knotenspannungsverfahren

Was kommt als Nächstes?

Im nächsten Kurstext setzen wir uns intensiv mit der Zweipoltheorie auseinander.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++