(ET3-06) Knotenspannungsverfahren – Erklärung – einfach erklärt

In diesem Kurstext stellen wir dir als angehenden Techniker ausführlich das Knotenspannungsverfahren vor.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET3-Netzwerkberechnung

Knotenspannungsverfahren – Überblick

“Das Knotenspannungsverfahren, manchmal auch Knotenpotentialverfahren genannt, ist ein Verfahren zur Berechnung von elektrischen Größen in linearen Netzwerken.”

Knotenspannungsverfahren - Netzwerkkabel — Knotenspannungsverfahren – Netzwerkkabel

Die Mischung macht’s…

Das Knotenspannungsverfahren ist ein Mix aus Knotenpunktsatz sowie Ohm’schem Gesetz.

Knotenspannungsverfahren – Sinn und Zweck

Das Ziel ist die Bestimmung der Spannungen zwischen den Knotenpunkten (Knotenspannungen) ausgehend von den Potentialen $\varphi$ der einzelnen Knotenpunkte.

Dabei wählt man einen Knotenpunkt frei aus und setzt dessen Potential auf den Wert $\varphi = 0$ .

Wenn du die Knotenspannungen kennst, dann kannst du die Zweigströme einfach berechnen.

Knotenspannungsverfahren – Vorgehensweise zur Lösung:

Zur Anwendung des Knotenspannungsverfahrens sollte folgende Punkte auf der Merkliste bearbeitet bzw. berücksichtigt werden:

1. Kennzeichne alle Knotenpunkte

2. Wähle einen Knotenpunkt, kennzeichne ihn mit 0 und setze den Wert für dessen Potential auf 0.

3. Stelle die Gleichung für die Knotenspannung $U_{\nu \mu}$ auf:
$U_{\nu \mu} = \varphi_{\nu} - \varphi_{\mu}$ .

4. Stelle die Gleichung zur Bestimmung der Zweigströme $I_{\nu \mu}$ nach dem Ohm’schen Gesetz auf, welche die Gleichungen für die Knotenspannungen beinhaltet:
$I_{\nu \mu} = G_{\nu \mu} \cdot U_{\nu \mu}$

5. Beachte bei 4. die gegebene Quellenspannung.

6. Stelle die unabhängigen Knotenpunktgleichungen der Ströme nach dem Knotenpunktsatz auf.

7. Löse das sich ergebende Gleichungssystem.

Beispiel: Berechnung mit dem Knotenspannungsverfahren

Damit dir das Verständnis auf dieses Verfahren vereinfacht wird, spielen wir nun die Vorgehensweise einfach einmal durch.

Beispiel: Knotenspannungsverfahren!

Im nächsten Bild siehst du ein Netzwerk, welches drei Knotenpunkte (A,B,C) besitzt. Auch die Zählpfeile für die Quellenspannung und die Zweigströme finden sich in der Zeichnung wieder.

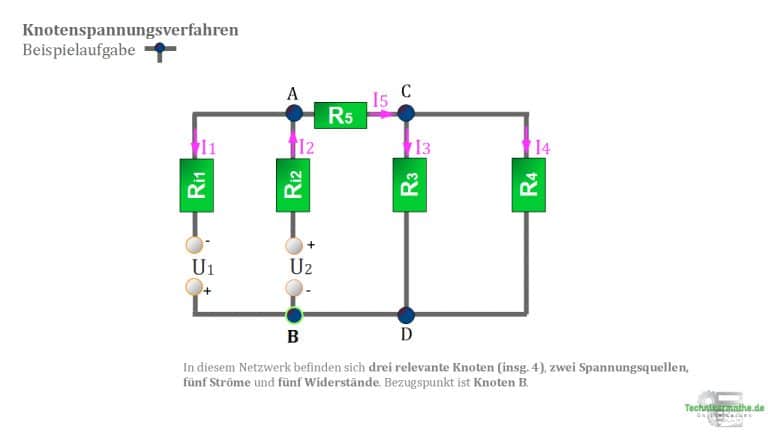
Knotenspannungsverfahren - Beispielaufgabe — Knotenspannungsverfahren – Beispielaufgabe

Wir wählen zufällig den Knotenpunkt B aus als Bezugspunkt.
Somit wird das Potential von Knotenpunkt B → $\varphi_B = 0$

Aufstellen der Gleichungen

Mit dem Maschensatz stellen wir nun die Gleichungen für die Zweigströme auf.

Zum besseren Verständnis schaue dir die nächste Abbildung an. Hier ist der Umlaufsinn festgelegt.

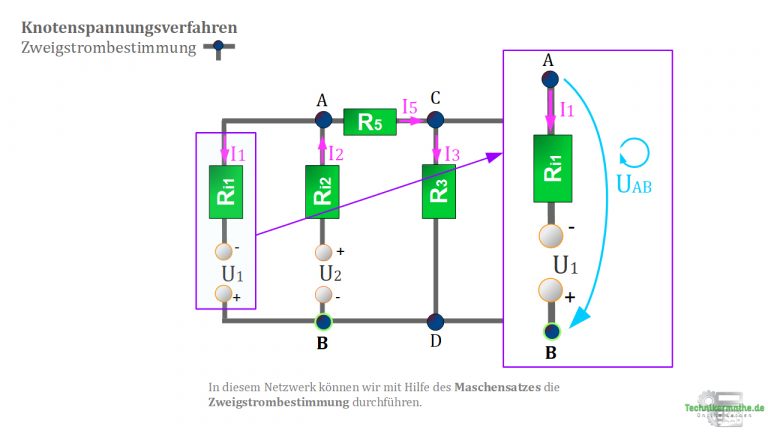
Zweigstrombestimmung - Knotenspannungsverfahren — Zweigstrombestimmung – Knotenspannungsverfahren

Gleichung des Zweigstroms aus der letzten Abbildung:

$I_1 \cdot R_{i1} - U_1 - U_{AB} = 0$

Auflösen der Gleichung nach $I_1$

$I_1 = \frac{ U_1 + U_{AB}}{R_{i1}}$

sowie

$I_1 = \frac{1}{R_{i1}} \cdot (U_1 + U_{AB})$

Mit $U_{AB} = \varphi_A - \varphi_B)$

Angabe mit Leitwerten

$I_1 = G_{i1} \cdot ( U_1 + \varphi_A - \varphi_B)$

Die andere Polung der Spannungsquelle muss von dir berücksichtigt werden.

Ohne Fleiß, kein…. Ergebnis!

Jetzt beginnt die wirkliche Arbeit für dich. Du musst nun das Gleichungssystem zu unserem Netzwerk aufstellen.

Dieses umfasst 2 Gleichungen für die Knotenspannungen und 5 Gleichungen für die Zweigströme:

Knotenspannungsverfahren – Gleichungssystem

Jetzt stellen wir zwei Gleichungssysteme für die Knotenspannungen und die Zweigströme auf.

Knotenspannungen:

$K1: U_{AB} = \varphi_A - \varphi_B = \varphi_A , \text{weil} \varphi_B = 0$

sowie

$K2: U_{CB} = \varphi_C - \varphi_B = \varphi_C ,\text{weil} \varphi_B = 0$

Zweigströme

$Z1: I_1 = G_{i1} \cdot ( U_{AB} + U_1) = G_{i1} \cdot ( \varphi_A + U_1)$

sowie

$Z2: I_2 = G_{i2} \cdot (- U_{AB} + U_2) = G_{i2} \cdot (- \varphi_A + U_2)$

sowie

$Z3: I_3 = G_{3} \cdot U_{CB} = G_{3} \cdot \varphi_C$

sowie

$Z4: I_4 = G_{4} \cdot U_{CB} = G_{4} \cdot \varphi_C$

sowie

$Z5: I_5 = G_{5} \cdot U_{AC} = G_{5} \cdot (\varphi_A - \varphi_C$

Aufstellen der Knotenpunktgleichungen der Ströme

$A: I_2 - I_1 - I_5 = 0$

sowie

$B: I_5 - I_3 - I_4 = 0$

Im nächsten Schritt lösen wir das Gleichungssystem nach den unbekannten Größen

$\varphi_A$ und $\varphi_B$ auf und können die Zweigströme bestimmen

Was kommt als Nächstes?

Nachdem du nun die Vorgehensweise beim Knotenspannungsverfahren kennst, möchten wir dieses Thema nochmals vertiefen. Deshalb folgt im nächsten Kurstext ein ausführliches Zahlenbeispiel zum Thema. Außerdem findest du im Ordner Webinar ein umfangreiches Live-Meeting von 100 Minuten zu diesem Thema.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++