(ET3-05) Maschenstromverfahren – Beispiel auf Klausurniveau [Musterlösung]

Wie das Maschenstromverfahren funktioniert hast du ja bereits im vorherigen Kurstext erlernt nun betrachten wir eine typische Aufgabe in derer man Maschenströme nutzt, um eine gesuchte Größe berechnen zu können.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET3-Netzwerkberechnung

Genau nach dem Schema wie dir das Maschenstromverfahren in deiner Prüfung zum Techniker begegnen könnte. Die verwendete Rechenart ist der Gauß’sche Algorithmus.

Videoclip – Maschenstromverfahren

Im nächsten Video findest ein ausführliches Beispiel zum Maschenstromverfahren.

Maschenstromverfahren

Zum Nachlesen.

Beispiel: Maschenströme – Lösen mit dem Gaußschen Algorithmus

Aufgabenstellung: Maschenströme

Maschenströme im Verfahren nutzen um unbekannte Größe zu ermitteln.

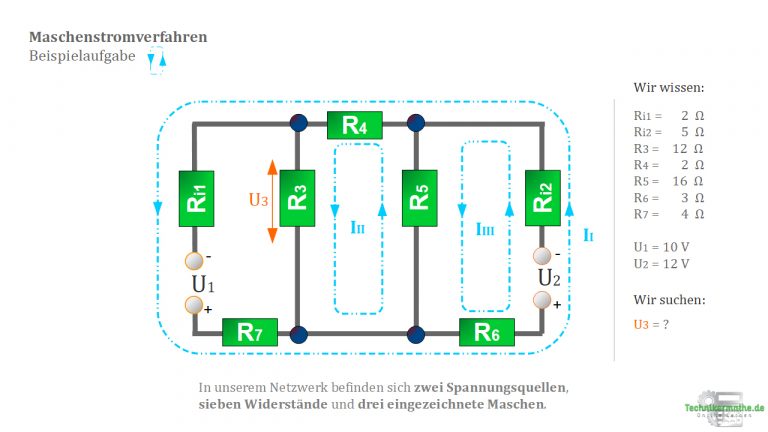
Wir haben ein Netzwerk gegeben wie in der nächsten Abbildung dargestellt.

Die Elemente des Netzwerks weisen folgende Zahlenwerte auf.
Die Teilspannungen sind: $U_1 = 10 V, U_2 = 12 V$

Die Teilwiderstände sind: $R_{i1} = 2 \Omega, R_{i2} =2 \Omega, R_3 = 12 \Omega, R_4 = 2 \Omega, R_5 = 16 \Omega, R_6 = 3 \Omega, R_7 = 4 \Omega }$

Deine Aufgabe besteht nun darin die Teilspannung $U_3$ am Widerstand $R_3$ zu berechnen.

1. Lesen der Aufgabenstellung (Vorarbeit) – Maschenströme

Du musst nun die Teilspannung $U_3$ berechnen.

2. Sichten der Skizze (Vorarbeit) – Maschenströme

Markieren/Einzeichnen der notwendigen Größe

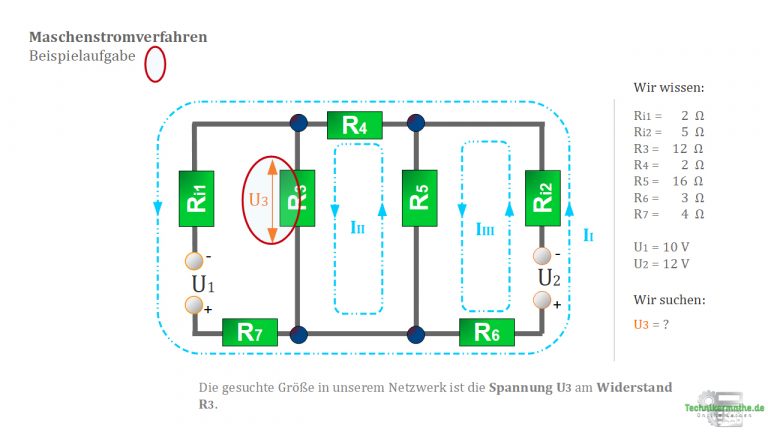
Maschenströme - Beispielaufgabe — Maschenströme – Beispielaufgabe

3. Aufstellen der Maschengleichungen – Maschenströme

3.1 Masche mit Maschenstrom $I_I$

$- U_1 + U_2 + I_I \cdot (R_{i1} + R_7 + R_6 + R_{i2} + R_4) - I_{II} R_4 - I_{III} \cdot (R_{i2} + R_6) = 0$

3.2 Masche mit Maschenstrom $I_{II}$
$- I_I \cdot R_4 + I_{II} \cdot (R_3 + R_4 + R_5) - I_{III} \cdot R_5 = 0$

3.3 Masche mit Maschenstrom $I_{III}$
$- I_I \cdot (R_{i2} + R_6) - I_{II} \cdot R_5 + I_{III} (R_5 + R_6 + R_{i2}) - U_2 = 0$

4. Umstellen der Gleichung 3.1 nach $(U_1 - U_2)$

$I_I \cdot (R_{i1} + R_7 + R_6 +R_{i2} + R_4) - I_{II} \cdot R_4 - I_{III} \cdot (R_{i2} + R_6) = U_1 - U_2$

5. Umstellen der Gleichung 3.3 nach (U_2)

$- I_I \cdot (R_{i2} + R_6) - I_{II} \cdot R_5 + I_{III} (R_5 + R_6 + R_{i2}) = U_2$

6. Einsetzen der Zahlenwerte in die Gleichungen 4., 3.2 und 5

6.1 Zahlenwerte in 4. einsetzen:
$I_I \cdot (2 \Omega + 3 \Omega + 4\Omega + 5 \Omega+ 2 \Omega) - I_{II} \cdot 2 \Omega- I_{III} \cdot ( 5 \Omega+ 3 \Omega) = 10 V - 12 V$

6.2 Zahlenwerte in 3.2 einsetzen:
$- I_I \cdot 2 \Omega+ I_{II} (12 \Omega+ 2 \Omega+ 16 \Omega) - I_{III} \cdot 16 \Omega= 0$

6.3 Zahlenwerte in 5. einsetzen:
$- I_I \cdot (5 \Omega+ 3 \Omega) - I_{II} \cdot 16 \Omega+ I_{III} \cdot (16 \Omega+ 3 \Omega+ 5 \Omega) = 12 V$

7. Zusammenfassen der Gleichungen unter 6.

7.1 Zusammenfassen der Gleichung 6.1:

$16 \Omega \cdot I_I - 2 \Omega \cdot I_{II} - 8 \Omega \cdot I_{III} = - 2 V$

7.2 Zusammenfassen der Gleichung 6.2:
$- 2 \Omega \cdot I_I + 30 \Omega \cdot I_{II} - 16 \Omega \cdot I_{III} = 0$

7.3 Zusammenfassen der Gleichung 6.3:
$- 8 \Omega \cdot I_I - 16 \Omega \cdot I_{II} + 24 \Omega \cdot I_{III} = 12 V$

8. Anwendung des Gaußschen Algorithmus

Mit Hilfe des Gaußschen Algorithmus lösen wir nun dieses Gleichungssystem. In der nächsten Abbildung siehst du eine Matrix, die es nun von uns zu bearbeiten gilt.

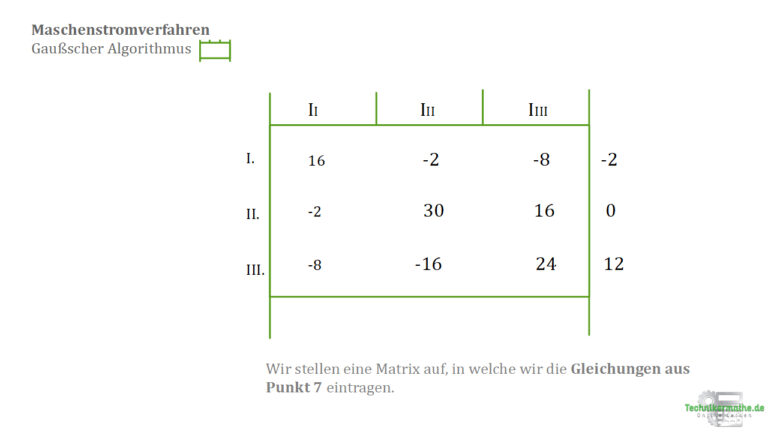
Maschenströme - Algorithmus nach Gauß — Maschenströme – Algorithmus nach Gauß

Die Matrix kennzeichnet eine Diagonale (rot).

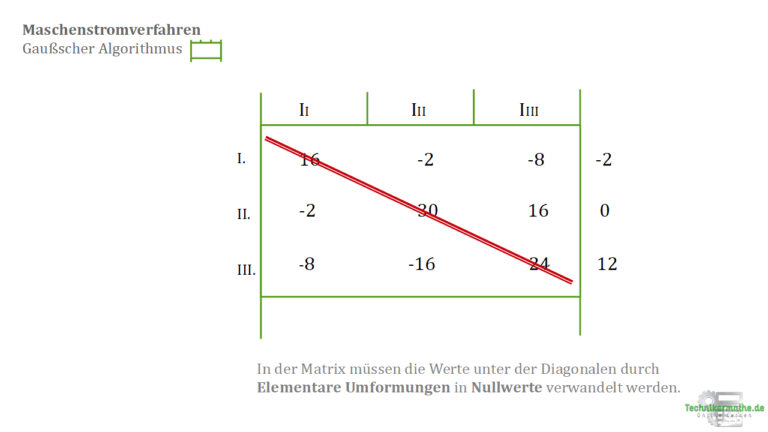
Maschenstromverfahren - Gaußscher Algorithmus — Maschenstromverfahren – Gaußscher Algorithmus

Die Werte unter der Diagonalen (-2, -8, -16) müssen wir nun mit „elementaren Umformungen“ in mehreren Schritten in Nullwerte verwandeln.

8.1 Start Zeile II.
Wir multiplizieren die Gleichung (und alle Werte) in Zeile II mit dem Faktor 8 und addieren sie zur Gleichung I in Zeile 1.

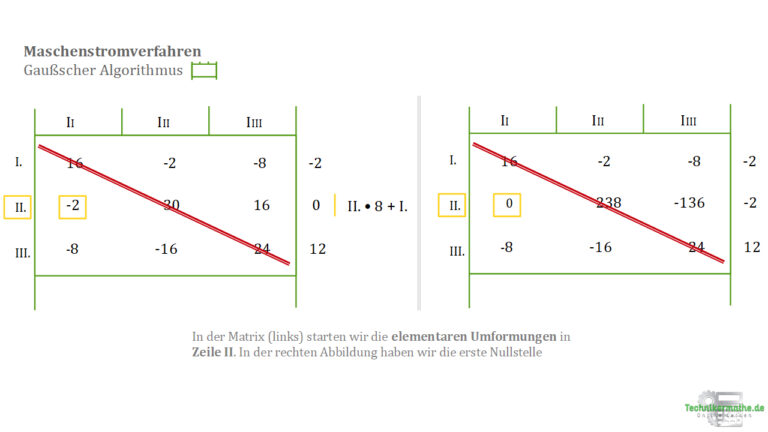
In der neuen Matrix konnten wir somit bereits aus der -2 eine 0 erzeugen.

8.2 Weiter mit Zeile III
Jetzt wollen wir die -8 eliminieren. Dazu multiplizieren wir die Gleichung in Zeile 3 mit dem Faktor 2 und addieren sie zu Gleichung I

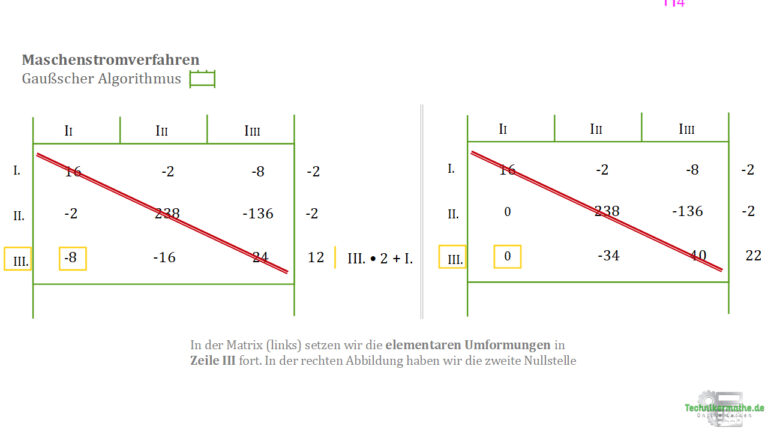
Mit diesem Schritt haben wir nun die – 8 in eine Null überführt.

8.3 Nun geht es erneut weiter mit Zeile III
Es fehlt uns lediglich die -34, die in eine Null verwandelt werden soll. Dieser Schritt gelingt, indem wir die Zeile 3 mit 7 multiplizieren und die Zeile 2 dazu addieren.

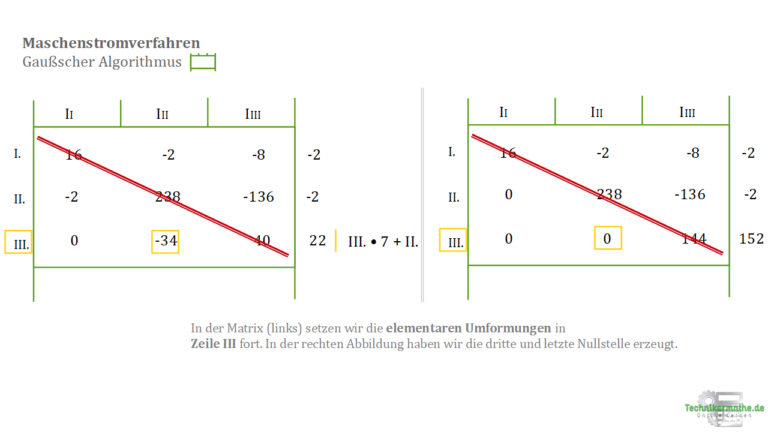
Maschenstromverfahren - Gaußscher Algorithmus 2 — Maschenstromverfahren – Gaußscher Algorithmus 2

8.4 Alles Zahlenwerte unterhalb der Diagonalen der Matrix konnten eliminiert und in eine Null umgewandelt werden.

9. Transformierte Gleichungen auflösen

9.1 Gleichung, Zeile III:
Wir nehmen nun die Letzte Zeile aus der Matrix und stellen die erste Gleichung auf. Hier ist unser Vorteil, dass lediglich $I_{III}$ auftritt:

$0 \cdot I_I + 0 \cdot I_{II} + 144 \cdot I_{III} = 152$

Einsetzen:

$+ 144 \cdot I_{III} = 152 | : 144$

Auflösen:

$I_{III} = 1,06 A$

9.2 Gleichung, Zeile II:
Wir schreiben die Gleichung auf und setzen den gerade ermittelten Wert für $I_{III}$ ein:

$0 \cdot I_I + 238 \cdot I_{II} - 136 \cdot I_{III} = - 2$

Einsetzen:

$+ 238 \cdot I_{II} - 136 \cdot 1,06 = - 2$

anschließend

$+ 238 \cdot I_{II} - 144,16 = -2 | + 144,16$

und

$+ 238 \cdot I_{II} = 142,16 | : 238$

Auflösen:

$I_{II} = 0,597 A$

9.3 Letzter Lösungsschritt:
Für die Lösung benötigen wir $I_{I}$ nicht und können mit unserem Zwischenergebnis aus 9.2 ganz locker $U_3$ bestimmen:

$U_{3} = I_{II} \cdot R_3 = 0,597 A \cdot 12 \Omega = 7,16 V$

10. Formuliere den Antwortsatz – Maschenströme

Somit hat der gesuchte Strom einen Wert von

$U_{3} = 7,16 V$ .

Was kommt als Nächstes?

Im nächsten Kurstext stellen wir dir das Knotenspannungsverfahren im Detail vor.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++