(ET3-04) Maschenstromverfahren – [Erklärung, Formeln, Beispielaufgabe, Lernclip]

In diesem Kurstext erklären wir dir als angehenden Techniker ausführlich und einfach das Maschenstromverfahren. Dabei stellen wir dir auch ein ausführliches Lösungsschema vor.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET3-Netzwerkberechnung

Maschenstromverfahren – Überblick

“Das Maschenstromverfahren dient dem Techniker zur Berechnung von Netzwerken sowie Strömen und Spannungen.”

Maschenstromverfahren - Verteilerkasten in Osnabrück — Maschenstromverfahren – Verteilerkasten in Osnabrück

Hier wird jeder unabhängigen Masche ein geschlossener Maschenstrom zugeordnet. Ein Maschenstrom ist lediglich eine Hilfsgröße. Mit Hilfe eines linearen Gleichungssystems kannst du die Maschenströme lösen und anschließend die gesuchten Größen ermitteln.

Verfahren – Tipps und Tricks

Das solltest du dir auf jeden Fall merken..

Hier gilt es folgendes zu beachten:

1. Dort wo ein Zweig lediglich von einer Masche berührt wird, ist der Maschenstrom gleich dem Zweigstrom.

$I_1 = I_I$

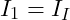
sowie

2. Dort wo ein Zweig von zwei Maschen berührt wird, überlagern sich die Maschenströme. Dann ist der Zweigstrom die Summe der beiden einzelnen Maschenströme, sofern beide Maschen einen umgekehrten Umlaufsinn aufweisen.

$I_2 = I_I + I_{II}$

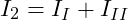
sowie

3. Besitzen die beiden Maschen hingegen den gleichen Umlaufsinn, so entspricht der Zweigstrom der Differenz der beiden einzelnen Maschenströme.

$I_2 = I_I - I_{II}$

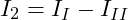
Die Stromrichtung wird willkürlich gewählt und geht positiv in eine Berechnung ein.

Merk’s dir!

Der Maschenstrom (bspw. $I_I$ ) muss dabei nicht zwangsläufig dem Zweigstrom (bspw. $I_1$ ) entsprechen. Aber beachte immer die tiefergestellten Zeichen!!

undefiniert

Problemfall - Stromquelle

Eigentlich kann man mit der Berechnung der Maschenströme direkt starten, gäbe es da nicht auch Netzwerke in denen neben den Spannungsquellen auch noch eine Stromquelle auftaucht. Letztere musst du dann vor dem Start der Berechnung in eine Spannungsquelle umwandeln.

In der nächsten Abbildung entdeckst du ein Netzwerk mit drei voneinander unabhängigen Maschen mit ihren jeweiligen Maschenströmen $I_I, I_{II}, I_{III}$ .

Maschenstromverfahren - 3 Maschen — Maschenstromverfahren – 3 Maschen

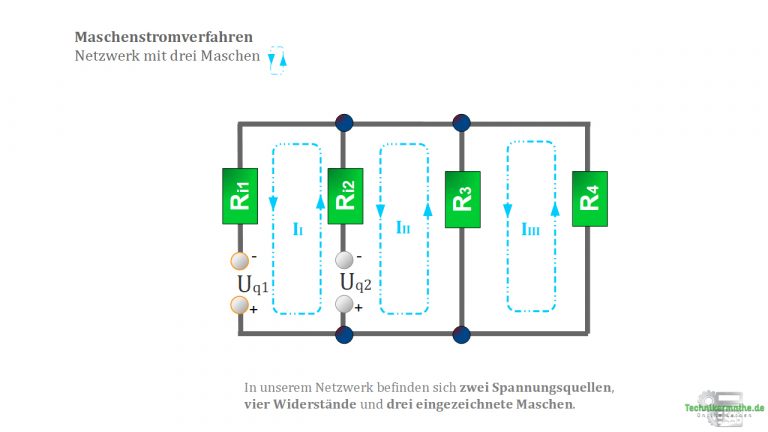
Die Zweige $R_{i2}$ und $R_{4}$ haben eine Besonderheit, denn sie gehören im Gegensatz zu den anderen Zweigen jeweils zwei Maschen an.

Somit überlagern sich hier die Maschenströme und ihre Summe entspricht dem wirklich fließenden Zweigstrom.

Maschenstromverfahren – Überlegungen und Hinweise

Daraus leiten wir dann ab.

1. Im Widerstand $R_{i2}$ ist der Zweigstrom $I_2$ gleich der Summe von den Maschenströmen $I_I + I_{II}$

2. Im Widerstand $R_{3}$ ist der Zweigstrom $I_3$ gleich der Summe von den Maschenströmen $I_{II} - I_{III}$ – Aber vorausgesetzt: Die Richtung des Zweigstroms $I_3$ stimmt mit der Richtung des Maschenstroms $I_{II}$ durch $R_3$ überein.

3. Der Strom durch $R_{i1}$ ist gleich dem Maschenstrom $I_I$ .

4. Der Strom durch $R_4$ ist gleich dem Maschenstrom $I_{III}$

Berechnung der Zweigströme

Mit dieser Vorgehensweise erhältst du so viele unbekannte Maschenströme, wie unabhängige Maschen verfügbar sind.

Somit können ganz einfach die Zweigströme

– direkt (Vergleich von $R_{i1}$ und $R_4$ )

durch

– simple Addition ( $R_{i2}$ )

oder

– simple Subtraktion ( $R_{3}$ )
bestimmt werden.

Merk’s dir!

Obwohl die allgemeine Netzwerkberechnung mit den Kirchhoff’schen Sätzen häufig genutzt wird, hat das Verfahren den Vorteil, dass keine Knotenpunktgleichungen aufgestellt werden müssten. So vereinfacht sich die Berechnung und wir werden wesentlich schneller mit einer Berechnung fertig.

Mega gut!…

Ein weiterer Vorteil besteht darin, dass wir Maschenströme so wählen können, dass sie durch den uns interessierenden Zweig nur ein Maschenstrom fließen.

Beispiel: Berechnung mit dem Maschenstromverfahren

Ausgehend von unserer Abbildung möchten wir nun direkt den Strom durch $R_{i2}$ berechnen.

Maschenstromverfahren – Variante 1

Hierzu passen wir unsere Abbildung dahingehend an, dass wir

eine neue Masche mit dem Maschenstrom 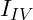$I_{IV}$ einführen ( 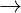$\rightarrow$ Diese umläuft das Netzwerk)

sowie

die Masche mit dem Maschenstrom 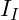$I_{I}$ entfernen.

Maschenstromverfahren – Variante 2

eine neue Masche mit dem Maschenstrom 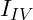$I_{IV}$ einführen ( 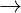$\rightarrow$ Diese umläuft das Netzwerk)

sowie

die Masche mit dem Maschenstrom 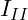$I_{II}$ entfernen.

Maschenstromverfahren – Vorgehensweise zur Lösung

Zur Anwendung des Verfahren sollte folgende Merkliste bearbeitet bzw. berücksichtigt werden.

1. Jeder unabhängigen Masche ordnest du einen Maschenstrom zu.

2. Die Richtung des Maschenstroms kannst du frei wählen.

3. Du musst die Richtung des Maschenstroms immer positiv angeben.

4. Wähle die Masche so aus, dass immer nur ein Maschenstrom durch den interessanten Zweig fließt.

5. Stelle die Gleichungen für die ausgewählten Maschen nach dem Maschensatz nach Kirchhoff auf.

6. Berechne aus dem Gleichungssystem der Maschensätze den/die gesuchten Strom/Ströme.

Übungsbeispiel: Maschenstromverfahren – Durchführung

Maschenstromverfahren - Netzwerk — Maschenstromverfahren – Netzwerk

Aufgabenstellung und bekannte Größen

Beispiel: Maschenstromverfahren

In dem vorliegenden Netzwerk soll der Teilstrom $I_I$ durch den Widerstand $R_{i1}$ berechnet werden.

Gegeben sind die Teilspannungen $U_1 = 75 V$ und $U_2 = 90 V$ , sowie die Teilwiderstände $R_{i1} = 2,1 \Omega$ , $R_{i2} = 2,8 \Omega$ , $R_3 = 140 \Omega$ und $R_4 = 120 \Omega$

1. Lesen der Aufgabenstellung (Vorarbeit)

Du musst nun den Teilstrom $I_I$ berechnen.

2. Sichten der Skizze (Vorarbeit)

Einzeichnen der notwendigen Größe

3. Aufstellen der Maschengleichungen nach dem Maschensatz (rechnerisch)

3.1. – Masche mit dem Maschenstrom $I_I$

$- U_1 + U_2 + I_I \cdot ( R_{i1} + R_{i2}) +I_{II} \cdot R_{i2} = 0$

3.2. – Masche mit dem Maschenstrom $I_{II}$

$+ U_2 + I_I \cdot R_{i2} +I_{II} \cdot ( R_{i2} + R_3) +I_{III} \cdot R_{3} = 0$

3.3. – Masche mit dem Maschenstrom $I_{III}$

$- I_{II} \cdot R_3 +I_{III} \cdot ( R_3 + R_4) = 0$

4. Einsetzen der bekannten Größen in die Maschengleichungen (rechnerisch)

4.1. – Masche mit dem Maschenstrom $I_I$

$- 75 V + 90 V + I_I \cdot ( 2,1 \Omega+ 2,8 \Omega) +I_{II} \cdot 2,8 \Omega= 0$

4.2. – Masche mit dem Maschenstrom $I_{II}$

$+ 90 V + I_I \cdot 2,8 \Omega +I_{II} \cdot (2,8 \Omega + 140 \Omega) +I_{III} \cdot 140 \Omega = 0$

4.3. – Masche mit dem Maschenstrom $I_{III}$

$- I_{II} \cdot 140 \Omega + I_{III} \cdot ( 140 \Omega + 120 \Omega ) = 0$

5. Optional – Umstellen und Zusammenfassen der Maschengleichungen (rechnerisch)

Trennung von Spannung und (Stromstärke + Widerstand)

5.1. – Masche mit dem Maschenstrom $I_I$

$- 15 V = 4,9 \Omega \cdot I_I + 2,8 \Omega \cdot I_{II}$

5.2. – Masche mit dem Maschenstrom $I_{II}$

$- 90 V = 2,8 \Omega \cdot I_I + 142,8 \Omega \cdot I_{II} + 140 \Omega \cdot I_{III}$

5.3. – Masche mit dem Maschenstrom $I_{III}$

$0 = -140 \Omega \cdot I_{II} + 260 \Omega \cdot I_{III}$

6. – Überführung der Gleichungen ineinander (rechnerisch)

Letztlich auflösen nach $I_I$ – Beachte bei den Einheiten: $\frac{V}{\Omega } = A$

6.1 – Gleichung 5.1 nach $I_{II}$ auflösen

$I_{II} = - \frac{15 V}{2,8 \Omega } - {4,9 \Omega \cdot I_I}{2,8 \Omega } = - 5,36 A - 1,75 I_I$

6.2 – Gleichung 5.2 nach $I_{III}$ auflösen

$-90 V = 2,8 \Omega \cdot I_I - 142,8 \Omega \cdot I_{II} = -140 \Omega \cdot I_{III} | : -140$

$I_{III} = 0,643 A + 0,02 I_I + 1,02 I_{II}$

6.3 – Einsetzen von 6.1 in 6.2

$0,643 A + 0,02 I_I +1,02 (-5,36 A - 1,75 I_I) = I_{III}$

$0,643 A + 0,02 I_I - 5,4672 A - 1,785 I_I = I_{III}$

6.4 – Einsetzen von 6.3 und 6.1 in 5.3

$0 = -140 \Omega \cdot (-5,36 A - 1,75 I_I) + 260 \Omega \cdot (0,643 A + 0,02 I_I - 5,4672 A - 1,785 I_I)$

6.5 – Zusammenfassen und Auflösen von 6.4 nach $I_I$

$0 = 750,4 \Omega A + 245 \Omega \cdot I_I + 167,18 \Omega A + 5,2 \Omega I_I - 1421,47 \Omega A - 464,1 \Omega \cdot I_I$

$- 750 \Omega A - 167,18 \Omega A + 1421,47 \Omega A = 245 \Omega \cdot I_I + 5,2 \Omega \cdot I_I - 464,1 \Omega \cdot I_I$

folglich

$503,89 \Omega A = -213,9 \Omega \cdot I_I$

Beide Seiten der Gleichung durch $- \Omega$ dividieren.

aufgelöst ergibt

$-2,356 A =I_I$

7. Formuliere den Antwortsatz:

Somit hat der gesuchte Strom einen Wert von $I_I = -2,36 A$ +

8. Video zum Maschenstromverfahren

Im nächsten Video findest du noch mal eine Zusammenfassung des Kurstextes und zusätzliche Informationen zum Verfahren.

Maschenstromverfahren

Was kommt als Nächstes?

Im nächsten Kurstext folgt ein ausführliches Beispiel mit Zahlenwerten zu diesem Verfahren.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++