(ET3-03) Überlagerungssatz – einfach erklärt [Erklärung, Lernclip, Beurteilung]

In diesem Kurstext erklären wir dir als angehender Techniker/ Ingenieur ausführlich den Überlagerungssatz.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET3-Netzwerkberechnung

Überlagerungssatz – Erklärung

“Der Überlagerungssatz besagt, dass die Berechnung für jede elektrische Quelle getrennt erfolgen kann, wobei alle anderen idealen Quellen auf den Wert Null gesetzt werden.”

Überlagerungssatz – Grundlegendes

Wir stellen uns ein Netzwerk vor mit lediglich linearen Widerständen und mehreren Spannungsquellen vor.

Merk’s dir!

Der Überlagerungssatz besagt:
Für ein solches Netzwerk wie oben beschrieben gilt, dass sich der Strom eines Maschenzweiges aus einer von Summe von Teilströmen zusammensetzt. Dabei erzeugt jede Spannungsquelle in jedem Zweig einen Teilstrom.

Diese Überlagerung der Teilströme ist vorzeichenbehaftet, was bedeutet, dass die einzelnen Vorzeichen beachtet werden müssen. Letztlich ergibt die Überlagerung den Gesamtstrom in diesem Zweig.

Merk’s dir!

Beim Überlagerungssatz erhalten Ströme, die entgegensetzt fließen ein negatives Vorzeichen und sind in der Berechnung auch so halten.

Überlagerungssatz – Vorgehensweise zur Lösung

Zur Anwendung des Überlagerungssatzes sollte folgende Merkliste bearbeitet bzw. berücksichtigt werden.

1. Es gilt alles Spannungsquellen bis auf eine auszuschalten. Stichwort: Kursschluss!

2. Jeder Innenwiderstand einer Spannungsquelle besteht weiterhin in der Schaltung.

3. Berechne die unbekannten Teilströme in den Zweigen, aber gehe dabei von der verbliebenen Spannungsquelle aus.

4. Wiederhole den Vorgang für die weiteren Teilströme ausgehend von den anderen Spannungsquellen.

5. Die ermittelten Teilströme der Zweige müssen entsprechend ihrer Vorzeichen überlagert werden.

Wo brauche ich das?..

Der Überlagerungssatz findet auch Anwendung bei Schaltungen mit Spannungsquellen (unterschiedliche Frequenz) in der Wechselstromtechnik.

Übungsbeispiel: Überlagerungssatz anwenden

Beispiel: Überlagerungssatz

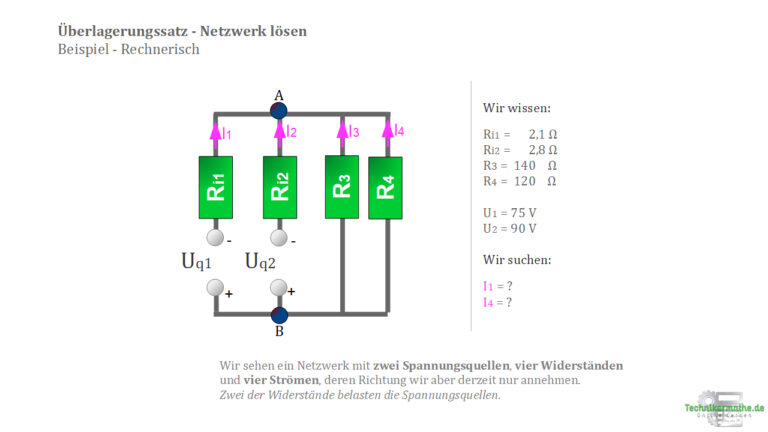
Überlagerungssatz - Netzwerk lösen — Überlagerungssatz – Netzwerk lösen

Wie haben hier ein Netzwerk gegeben, welches aus zwei parallelen Spannungsquellen besteht und vier Teilwiderständen von denen zwei Widerstände die Spannungsquellen belasten. Zudem liegen uns 4 Teilströme $I_1, I_2, I_3, I_4$ vor , sowie die Knoten A und B.

Aufgabenstellung und gegebene Größen

Aufgabenstellung

Die Spannungswerte sind angegeben mit

$U_1 = 75 V$

sowie

$U_2 = 90 V$

Die Werte für die Widerstände sind

$R_1 = 2,1 \Omega$

sowie

$R_2 = 2,8 \Omega$

sowie

$R_3 = 140 \Omega$

sowie

$R_4 = 120 \Omega$

Die Aufgabe für dich als angehender Techniker/ Ingenieur besteht nun darin, die Ströme $I_2$ und $I_4$ zu bestimmen.

Jetzt folgt der Lösungsweg nach dem obigen Schema in 9 Schritten.

Lösung

1. Lesen der Aufgabenstellung (Vorarbeit) – Überlagerungssatz

Du musst nun die beiden Teilströme berechnen.

2. Sichten der Skizze (Vorarbeit) – Überlagerungssatz

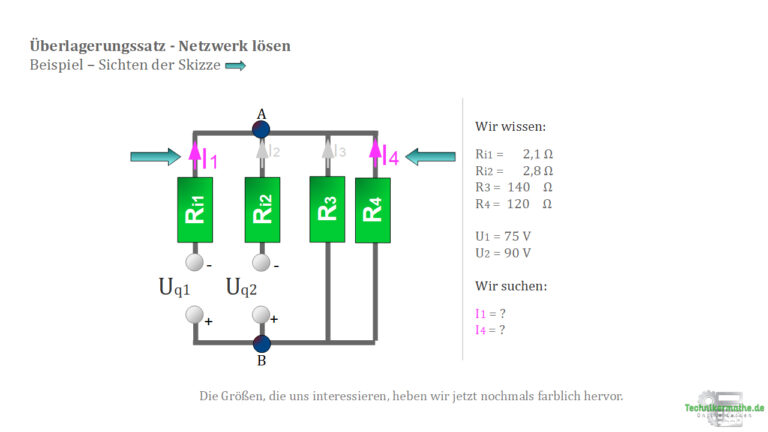
3. Kurzschließen der Quellenspannung 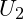$U_2$ und Eintragen der Teilspannungen $I'_2$ und $I'_4$ (Zeichnerisch)

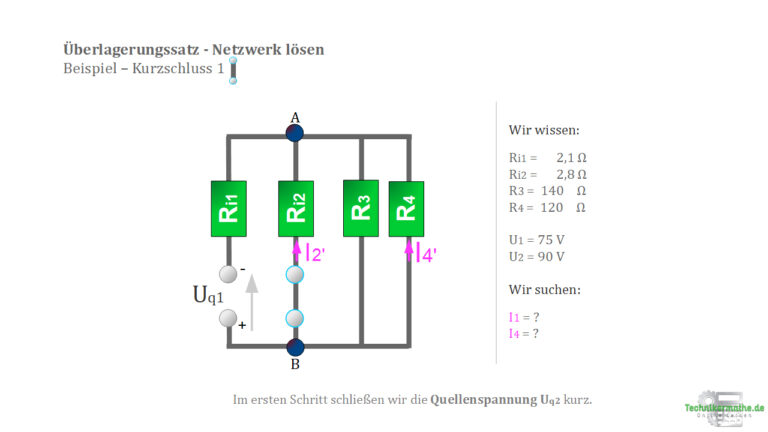
Überlagerungssatz - Kurzschluss erzeugen — Überlagerungssatz – Kurzschluss erzeugen

4. Anwendung der Spannungsteilerregel zur Berechnung der nicht kurzgeschlossenen Quellenspannung (Rechnerisch)

$U'_{BA} = U_1 \frac{ R_2 || R_3 || R_4}{ R_1 + (R_2 || R_3 || R_4)}$

mit
$R_3 || R_4 = \frac{140 \Omega \cdot 120 \Omega}{260 \Omega} = 64,6 \Omega$

sowie

$R_2 || R_3 || R_4 = \frac{ 64,6 \Omega \cdot 2,8 \Omega}{67,4 \Omega} = 2,69 \Omega$

sowie

$U'_{BA} = 75 V \cdot \frac{2,69 \Omega}{(2,1 \Omega + 2,69 \Omega} = 75 V \cdot \frac{2,69}{4,79} = 42,1 V$

5. Bestimmung der Teilströme $I'_2$ und $I'_4$ :

$I'_2 = \frac{U_{BA}}{R_2} = \frac{42,1 V}{2,8 \Omega} = 15,05 A$

sowie

$I'_4 = \frac{U'_{BA}}{R_4} = \frac{42,1 V}{120 \Omega} = 0,3505 A$

6. Kurzschließen der Quellenspannung 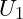$U_1$ und Eintragen der Teilspannungen $I''_2$ und $I''_4$ (Zeichnerisch)

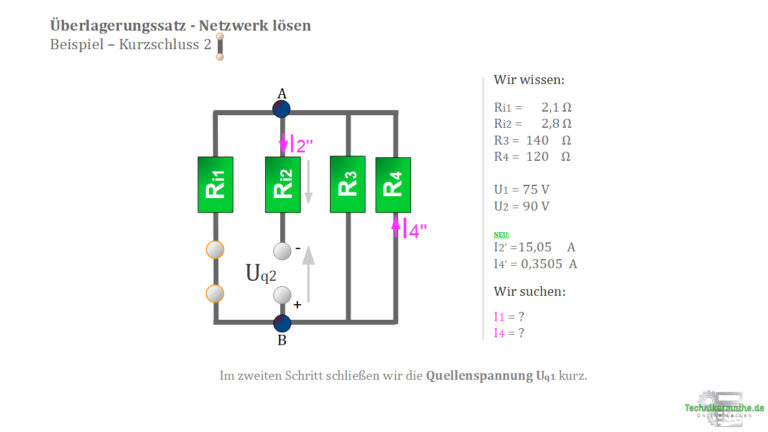
7. Anwendung des Ohm’schen-Gesetzes und des Maschensatzes zur Berechnung der Teilströme $I''_2$ und $I''_4$ der nicht kurzgeschlossenen Quellenspannung (Rechnerisch)

$I''_2 = \frac{U_2}{R_{12} + (R_1 || R_3 || R_4)}$

mit

$R_3 || R_4 = 64,6 \Omega$

sowie

$R_1 || R_3 || R_4 = \frac{2,1 \Omega \cdot 64,6 \Omega}{2,1 \Omega + 64,6 \Omega} = \frac{ 135,66 \Omega}{66,7 \Omega} = 2,04 \Omega$

sowie

$I''_2 = \frac{90 V}{2,8 \Omega + 2,04 \Omega} = \frac{90 V}{4,84 \Omega} = 18,6 A$

sowie

$U''_{AB} = U_2 - I''_2 \cdot R_2 = 90 V - 18,6 \cdot 2,8 V = 90 V - 52,1 V = 37,9 V$

sowie

$I''_4 = \frac{U''_{BA}}{R_4} = \frac{37,9 V}{120 \Omega} = 0,316 A$

8. Bestimmung der Zweigströme aus den Teilströmen unter Berücksichtigung der Richtung (Rechnerisch)

$I_2 = I''_2 - I'_2 = 18,6 A - 15,05 A = 3,65 A$

sowie

$I_4 = I''_4 - I'_4 = 0,3505 A + 0,316 A = 0,6665 A$

9. Verfassen der Antwort

Die gesuchten Ströme haben jeweils einen Wert von

$I_2 = 3,65 A$ (3,65 Ampere)

sowie

$I_4 = 0,6665 A$ (0,6665 Ampere)

Überlagerungssatz – Beurteilung

Vorteil:
1. Für Eine Spannungsquelle muss die Stromverteilung ermittelt werden und lediglich Widerstände werden genutzt.

2. Man verwendet mehrfach die Spannungsteilerregel oder ggf. die Stromteilerregel.

3. Eine Gruppenbildung der Spannungsquellen im Vorfeld ist möglich, wodurch die Wirkung gemeinsam überlagert werden kann.

Nachteil:
Liegen im Netzwerk mehrere Quellen vor, steigt auch der Berechnungsaufwand.

Was kommt als Nächstes?

Nachdem du jetzt den Überlagerungssatz kennengelernt hast, folgt im nächsten Kurstext mit dem Maschenstromverfahren, das nächste Verfahren zur Berechnung von Netzwerkgrößen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++