(ET2-28) Dreieck-Stern-Umformung [Prüfungsbeispiel]

Nachdem du die Dreieck-Stern-Umformung bereits erklärt bekommen hast, wollen wir nun gemeinsam eine typische Aufgabe zur Dreieck-Stern-Umformung berechnen, wie du sie als Techniker in deiner Prüfung vorfinden könntest. Dein Aufgabe ist, dass du dir hierzu die Abbildung anschaust und die gesuchte Größe mit Dreieck-Stern der Aufgabenstellung ermittelst.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zur Dreieck-Stern-Umformung und der Elektrotechnik findest du im Kurs: ET2-Gleichstromtechnik

Anschauungsbeispiel: Dreieck-Stern-Umformung

Beispiel: Dreieck-Stern-Umformung!

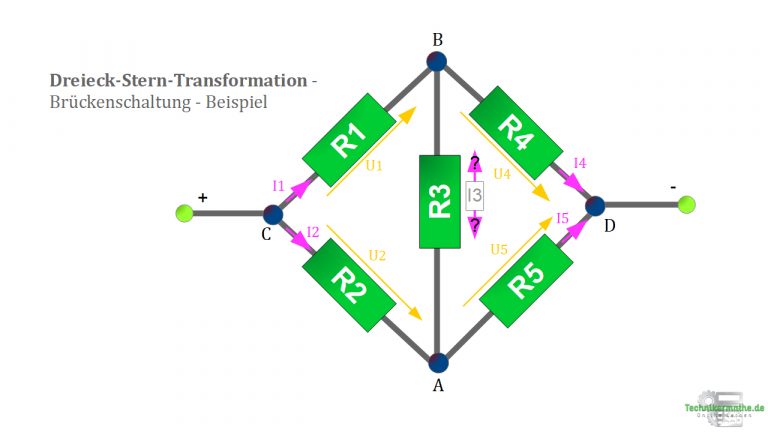
In der Abbildung findest du eine Brückenschaltung mit folgenden Widerständen inkl. Werten:

$R_1 = 20 k\Omega$

sowie

$R_2 = 50 k\Omega$

sowie

$R_3 = 30 k\Omega$

sowie

$R_4 = 15 k\Omega$

sowie

$R_5 = 25 k\Omega$

Die Spannung hat einen Wert von $U = 20 V$

Wir wollen nun wissen welchen Wert der Strom $I_3$ aufweist. Also $I_3 = ?$

Lösungsweg: Dreieck-Stern-Umformung

Die Lösung mit Hilfe der Dreieck-Stern-Umformung erfolgt in unserem Beispiel in 6 aufeinanderfolgenden Schritten.

1. Berechnen der Widerstände der äquivalenten Sternschaltung nach der bekannten Gleichung:

$\R'_3 = \frac{R_1 \cdot R_2}{R_1 + R_2 + R_3} = \frac{20 k\Omega \cdot 50 k\Omega}{(20 + 50 + 30) k\Omega} = 10 k\Omega$

sowie

$R'_2 = \frac{R_3 \cdot R_1}{R_3 + R_1 + R_2} = \frac{30 k\Omega \cdot 20 k\Omega}{(30 + 20 + 50) k\Omega} = 6 k\Omega$

sowie

$R'_1 = \frac{R_2 \cdot R_3}{R_2 + R_3 + R_1} = \frac{50 k\Omega \cdot 30 k\Omega}{(50 + 30 + 20) k\Omega} = 15 k\Omega$

2. Berechnen des Gesamtwiderstandes 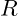$R$ vorliegenden Schaltung (inkl. $R_4$ & $R_5$ ):

$R = R'_3 + (R'_2 + R_4) || (R'_1 + R_5) = 10 k\Omega + \frac{21 k\Omega \cdot 40 k\Omega}{61 k\Omega} = 23,77 k\Omega$

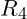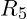3. Berechne den Gesamtstrom 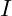$I$ , der den Widerstand $R'_3$ durchfließt nach Ohm’schem Gesetz:

$I = \frac{U}{R}= \frac{20 V}{23,77 k\Omega} = 0,842 mA$

4. Berechnung der Teilströme 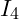$I_4$ und $I_5$ der Stern-Dreieck-Umformung:

Merk’s dir!

Warum? – Der Gesamtstrom verzweigt sich in die Zweige $R'_2 + R_4$ und $R'_1 + R_5$ .

Es gelten die Regeln der Stromverzweigung (Stromteilerregel) – Denn ein Teilstrom verhält sich zum Gesamtstrom, wie der von Teilstrom nicht durchflossene Widerstand zur Summe der Einzelwiderstände.

Wir müssen also die Teilströme durch $R'_2 + R_4$ und $R'_1 + R_5$ berechnen. Denn sie entsprechen den Strömen $I_4$ und $I_5$ , die in der vorliegenden Schaltung auch wirklich fließen.

$I_4 = I \frac{R'_1 + R_5}{R'_2 + R_4 + R'_1 + R_5} = 0,842 mA \cdot \frac{ (15 + 25) k\Omega}{(6 + 15 + 15 + 25) k\Omega}$

also

$I_4 = 0,552 mA$

sowie

$I_5 = I \frac{R'_2 + R_4}{R'_2 + R_4 + R'_1 + R_5} = 0,842 mA \cdot \frac{ (6 + 15) k\Omega}{(6 + 15 + 15 + 25) k\Omega}$

also

$I_5 = 0,29 mA$

5. Berechnen der Spannungen an 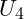$U_4$ und $U_5$ der Stern-Dreieck-Umformung:

Mit den beiden Strömen $I_4$ und $I_5$ lassen sich die Spannungen an den Widerständen $R_4$ und $R_5$ berechnen, nach dem Ohm’schen Gesetz:

$U_4 = I_4 \cdot R_4 = 0,552 mA \cdot 15 k\Omega = 0,552 \cdot 10^{-3} A \cdot 15 \cdot 10^{3} \Omega$

also

$U_4 = 8,28 V$

sowie

$U_5 = I_5 \cdot R_5 = 0,29 mA \cdot 25 k\Omega = 0,29 \cdot 10^{-3} A \cdot 25 \cdot 10^3 \Omega$

also

$U_5 = 7,25 V$

6. Berechnen des gesuchten Stroms 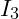$I_3$ nach der Dreieck-Stern-Umformung:

Mit dem Ohm’schen Gesetz können wir nun den gesuchten Strom bestimmen. Uns ist der Widerstand $R_3$ bekannt und die Spannung an diesem Widerstand ergibt sich aus der Differenz von $U_4 - U_5$ :

$I_3 = \frac{U_4 - U_5}{R_3} = \frac{(8,28 - 7,25) V}{30 \cdot 10^3 \Omega} = 34,4 \muA$

Es gilt, dass der Strom vom Knotenpunkt B hin zum Knotenpunkt A fließt .

Jetzt kennst du den ganzen Ablauf der Dreieck-Stern-Transformation.

Was kommt als Nächstes?

Nachdem wir nun ausreichend Erfahrung mit der Dreieck-Stern-Umformung haben, betrachten wir im nächsten Kurstext zuerst die Definition der Stern-Dreieck-Transformation. Anschließend folgt wieder ein ausführliches Beispiel zu diesem Thema!

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++