(ET2-27) Dreieck-Stern-Transformation [Grundlagen, Videoclips, Beispiele]

In diesem Kurstext stellen wir dir als angehenden Techniker / Ingenieur die Dreieck-Stern-Transformation detailliert vor.

Für ein optimales Verständnis helfen dir in diesem Kapitel drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET2-Gleichstromtechnik

Dreieck-Stern-Transformation – Überblick

Du hast ja bisher nur die Sternschaltung und die Dreieckschaltung als einzelne Schaltungsvarianten in einer Brückenschaltung und einem Drehstrommotor kennengelernt.

Jetzt erfährst du von uns wie man aus einer Dreieckschaltung eine Sternschaltung erzeugt.

Die Transformation ist immer dann sinnvoll, wenn dadurch die Schaltung am Ende so beschaffen ist, dass die Größen in Reihen– und Parallelschaltungen vorliegen. So können wir sie dann ganz einfach nach den bekannten Regeln lösen.

Jetzt wird es international…

Im internationalen Raum spricht man nicht selten von einer Delta-Star-Transformation oder vom Kennelly Theorem. Wenn du also zukünftig von diesen Begriffen liest, dann weißt du sofort, dass damit die Dreieck-Stern-Transformation gemeint ist.

Liegen gleiche Kennverhältnisse von äquivalenten Stern- und Dreieckschaltungen vor, so gilt dass der Widerstand zwischen einander entsprechenden Klemmenpaaren der Schaltungen wie im Bild dargestellt identisch sein muss.

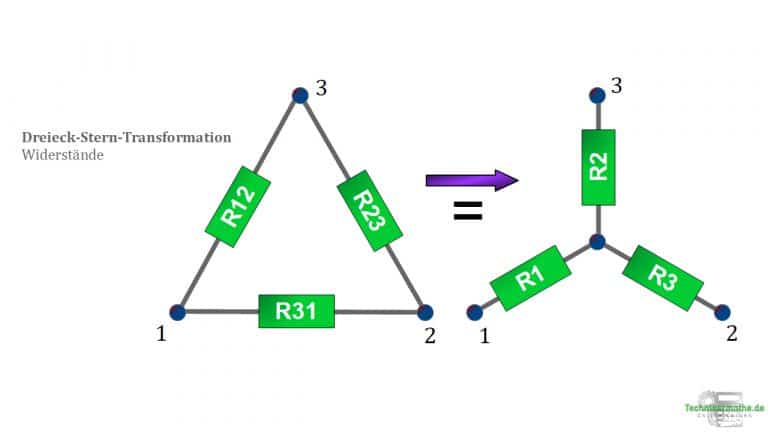
Wie sich das formal äußert, dass zeigt uns die nächste Tabelle:

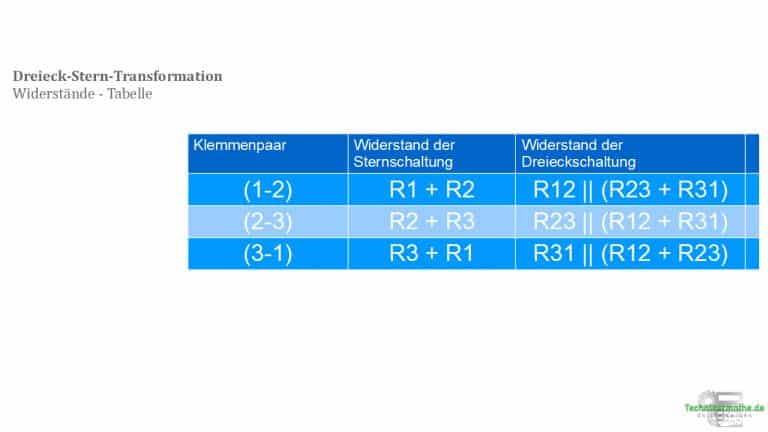
Widerstände – Gleichungen zur Transformation

Hier haben wir dir die Widerstände zwischen den Klemmenpaaren Zeile für Zeile bei Stern- und Dreieckschaltungen mit entsprechenden Gleichungen aufgeführt.

Jede Zeile in der Tabelle entspricht einer Gleichung. Wenn man nun zwei dieser Gleichungen miteinander addiert sowie dann die dritte Gleichung abzieht, so erhält man die Gleichungen zur Bestimmung der Widerstände der Sternschaltung:

$R_1 = \frac{R_{31} \cdot R_{12}}{R_{12} + R_{23} + R_{31}}$

sowie

$R_2 = \frac{R_{12} \cdot R_{23}}{R_{23} + R_{31} + R_{12}}$

sowie

$R_3 = \frac{R_{23} \cdot R_{31}}{R_{31} + R_{12} + R_{23}}$

Moment mal…

Als angehender Techniker hast du bestimmt schon gemerkt, dass die Nenner aller drei Gleichungen identisch sind.

Merkregel zur Dreieck-Stern-Transformation

Beziehen wir uns nun gedanklich wieder auf die Abbildung von Dreieck– und Sternschaltung, so können wir daraus eine Merkregel aufstellen:

Bitte nicht vergessen!…

$Sternwiderstand = \frac{\text{ Multiplizieren der am Knoten liegenden Dreieckswiderstände}}{\text{Addieren aller Dreieckswiderstände}}$

Leitwerte – Gleichungen zur Dreieck-Stern-Transformation:

Um die zugehörigen Leitwerte $G_1 , G_2 , G_3$ bestimmen zu können, bilden wir einfach den Kehrwert der obigen Gleichungen.

$G_1 = \frac{R_{12} + R_{23} + R_{31}}{R_{31} \cdot R_{12}} = \frac{1}{R_{31}} + \frac{R_{23}}{R_{12} \cdot R_{31}} + \frac{1}{R_{12}} = G_{31} + G_{12} + \frac{G_{31} \cdot G_{12}}{G_{23}}$

sowie

$G_2 = \frac{R_{23} + R_{31} + R_{12}}{R_{12} \cdot R_{23}} = \frac{1}{R_{12}}+ \frac{R_{31}}{R_{23} \cdot R_{12}} + \frac{1}{R_{23}} = G_{12} + G_{23} + \frac{G_{12} \cdot G_{23}}{G_{31}}$

sowie

$G_3 = \frac{R_{31} + R_{12} + R_{23}}{R_{23} \cdot R_{31}} = \frac{1}{R_{23}} + \frac{R_{12}}{R_{31} \cdot R_{23}} + \frac{1}{R_{31}} = G_{23} + G_{31} + \frac{G_{23} \cdot G_{31}}{G_{12}}$

Zyklusmuster der Indizes der Gleichungen

Merk’s dir!

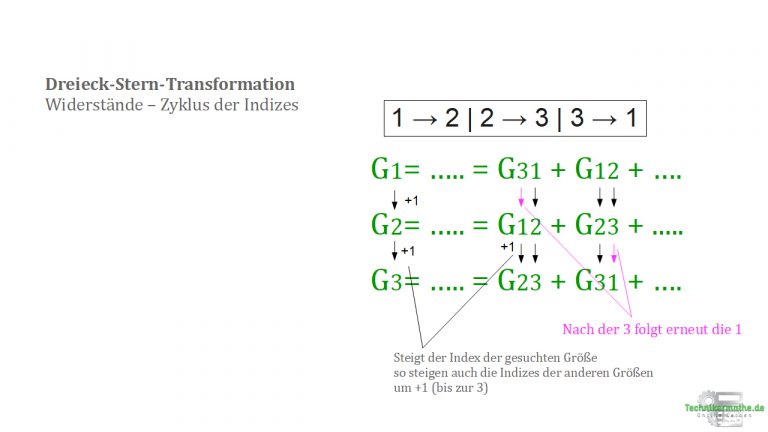
Wenn du die Indizes (die tiefgestellten Zahlen) alle Werte zyklisch vertauscht, so kannst du die jeweils Gleichungen für die Widerstände untereinander und jeweils die Gleichungen für die Leitwerte untereinander ineinander überführen.

Das Zyklusmuster der Indizes ist: 1 → 2 | 2 → 3 | 3 → 1

Dreieck-Stern-Transformation - Zyklus — Dreieck-Stern-Transformation – Zyklus

Was kommt als Nächstes?

Nachdem du diese Schaltungsart nun kennengelernt hast, stellen wir dir im nächsten Kurstext ein Beispiel zu dieser Schaltungsart im Detail vor und behandeln im übernächsten Kurstext den umgekehrten Fall und betrachten die Stern-Dreieck-Transformation.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++