(ET2-22) Brückenschaltung – Wheatstonesche Brücke [Grundlagen, Lernclips, Beispiele]

In diesem Kursabschnitt betrachten wir ausführlich die Wheatstonesche Brückenschaltung . In den Folgetexten stellen wir dir die spannungsgespeiste sowie stromgespeiste Brücke getrennt nacheinander vor. Ferner erklären wir dir die Schering-Brücke und Thomson-Brücke. 

Für ein optimales Verständnis helfen dir in diesem Kapitel drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema. 

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET2-Gleichstromtechnik

 

Brückenschaltung – Definition

 

Wheatstonesche Brückenschaltung – Grundlagen

Die Brückenschaltung nach Wheatstone, besser bekannt unter dem Namen Wheatstone’sche Brückenschaltung, ist eine Stromverzweigungsschaltung der besonderen Art.

 

Eine Brückenschaltung ist eine elektrische Schaltung. Die Besonderheit dieser Schaltung liegt darin, dass fünf Zweipole zusammengeschaltet sind. Die Form dieser Zusammenschaltung erinnert stark an ein groß geschriebenes H.

 

“Die horizontale Linie des H’s ist die Querverbindung und wird als Brückenzweig bezeichnet.”

 

Die Brückenschaltung besteht aus fünf Widerständen (Zweipolen) und aufgrund der Anordnung kann man auch von einer Parallelschaltung zweier Spannungsteiler sprechen, die über den Brückenzweig miteinander verbunden sind.

 

Kernaussage der Brückenschaltung

Ferner liegt die Besonderheit dieser Schaltung liegt darin, dass das Netzwerk  fünf Widerständen besteht, die einen Ring bilden wie in der nächsten Abbildung dargestellt.

 

“Die Brücke wird häufig von Technikern gewählt, da sie gegenüber einem einzelnen Spannungsteiler, den Vorteil birgt, dass im Brückenzweig sowohl die Spannung sowie den Strom durch Einstellung der Widerstände beeinflussen kann und sich zusätzlich die Polarität ändern lässt.”

 

Der Techniker unterscheidet:

• Viertelbrücken : Ein Widerstand ist variable.

sowie

• Halbbrücken: Zwei Widerstände sind variable.

sowie

• Vollbrücken: Vier Widerstände sind variable.

 

Der Strom , welcher durch fließt ist abhängig von den Spannungen an und , bzw. von den Spannungen an und .

Folglich sind die Größe und die Richtung des Stroms durch die Größe der Widerstände und festgelegt.

 

Gesetzmäßigkeiten der Brückenschaltung – Übersicht

Zur Bestimmung einzelner Größen einer Brücke empfehlen wir dir als Techniker folgende Liste zu berücksichtigen:

Dabei gilt:

• Wenn die Spannung an 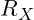größer als die an 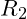ist, so fließt der Strom 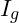in der obigen Schaltung sozusagen nach oben.

sowie

• Wenn die Spannung an 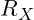kleiner als die an 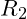ist, so fließt der Strom 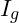entsprechend nach unten.

sowie

• Verändern wir nun die Widerstände 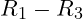um bestimmte Werte, so führt dies dazu dass die Spannung an Widerstand 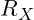der Spannung am Widerstand 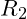entspricht.

sowie

• Daraus resultiert wiederum, dass jetzt auch die Spannung am Widerstand 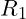der Spannung am Widerstand 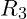entspricht.

und

• Somit ist der Strom 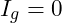und die Brücke ist abgeglichen, bzw. es liegt ein Abgleich vor.

 

“Der Widerstand ist unser Widerstand am Galvanometer. Hier solltest du die merken, dass ein Galvanometer den Nullpunkt in der Skalenmitte aufweist und sich somit einstellen lässt.”

 

Durch die angegebene Spannungsgleichheit von sowie gilt für .

 

Wheatstonesche Brücke – Formeln & Abgleichbedingung

Nehmen wir nun in Gedanken das Ohm’sche-Gesetz ( ) hinzu, so können wir die Gleichungen direkt umformulieren zu:

 

Nun verbinden wir die beiden Gleichungen indem wir einfach die erste Gleichung durch die 2. Gleichung dividieren und erhalten danach die Beziehung:

 

Wenn nun der Strom ist, so gilt und .

Somit kürzen sich die Spannungen aus der obigen Gleichung komplett heraus und es verbleibt die Abgleichbedingung:

          Abgleichbedingung 

 

Abgleichbedingung: Nach aufgelöst →

          Abgleichbedingung – abgeglichene Brücke ( nach aufgelöst)

 

Mit der letzten Gleichung haben wir eine Gleichung für eine abgeglichene Brücke verfasst.

 

Diese erlaubt uns einen unbekannten Widerstand unter Kenntnis der anderen Widerstände zu bestimmen.

 

“Die Gleichung besagt, dass bei einem Strom die Beziehung der Widerstände () zueinander, nicht von den zugehörigen Strömen abhängt und folglich auch nicht von der Größe und Richtung der Spannungsquelle.”

Diese Eigenschaft macht die Wheatstone’sche Brücke auch für den Wechselstrom anwendbar.

 

Anwendungsbereiche (Beispiele wie Schering-Brücke) für eine Wheatstone’sche Brücke

Nun stellen wir dir noch ein paar Bereiche vor in denen die Brückenschaltung bevorzugt eingesetzt wird.

 

Leistungselektronik:

• Brückengleichrichter (Wechselstrom in Gleichstrom)

sowie

• Endstufe in Verstärkern

 

Messtechnik:

• Thomson-Brücke (Messung kleiner Widerstände)

sowie

• Schering-Brücke (Messung der Kapazität in der Hochspannungstechnik

 

Technische Einsatzbereiche für die Wheatstone’sche Brückenschaltung

1. Widerstandsmessung: Die Schaltung kann verwendet werden, um den Wert eines unbekannten Widerstands 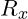zu bestimmen, indem sie mit bekannten Widerständen in einer Brückenschaltung kombiniert wird. Durch Messen der Spannungsdifferenz zwischen den Punkten der Brückenschaltung können Sie 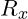berechnen.

2. Temperaturmessung: In der Temperaturmessung kann ein Thermistor (ein Temperatursensor mit einem Widerstand, der sich mit der Temperatur ändert) als 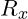 verwendet werden. Durch Ändern der Temperatur ändert sich der Widerstand des Thermistors, was zu einer Änderung der Spannungsdifferenz in der Brückenschaltung führt.

3. Drucksensoren: Drucksensoren können in Schaltungen integriert werden, um Druckänderungen in eine Änderung des Widerstands umzuwandeln. Dies ermöglicht die Messung von Druck durch die Messung der resultierenden Spannungsänderung.

4. Dehnungsmessstreifen (DMS): DMS werden oft in Waagen und Belastungssensoren verwendet. Sie ändern ihren Widerstand basierend auf der auf sie ausgeübten mechanischen Belastung. Indem man sie in eine Wheatstone-Brücken einbindet, kann man sehr genaue Messungen der Belastung vornehmen.

5. Feuchtigkeitssensoren: Einige Feuchtigkeitssensoren basieren auf Änderungen des Widerstands in Abhängigkeit von der Feuchtigkeit. Diese Sensoren können in Wheatstone-Brückenschaltungen integriert werden, um Feuchtigkeitsänderungen zu messen.

 

Was gibt es noch bei uns?

 

Dein Technikermathe.de-Team