(ET2-20) Der belastete Spannungsteiler

Nachdem wir dir bisher nur unbelasteten Spannungsteiler vorgestellt haben, folgt nun ein belasteter Spannungsteiler und die einfache Erklärung wie man diesen in einen unbelasteten Spannungsteiler überführt.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET2-Gleichstromtechnik

Belasteter Spannungsteiler - Schema — Belasteter Spannungsteiler

Belasteter Spannungsteiler – Grundlegendes

Wir schauen uns jetzt an was ein belasteter Spannungsteiler ist. Die Gleichung

$U_2 = \frac{ x \cdot P}{(1-x) \cdot P + x \cdot P} \cdot U_0 = x \cdot U_0$

besitzt immer nur dann eine Gültigkeit, wenn durch jeden unserer Widerstände ein identischer Strom fließt.

Auch muss der Spannungsteiler unbelastet betrieben werden und darf auf keinen Fall belastet werden.

Trotz aller Vorgaben, ist es gängige Praxis einen weiteren Widerstand $R$ am Ausgangs eines Spannungsteilers anzuschließen. Man bezeichnet diesen Widerstand dann entsprechend als Lastwiderstand $R_L$ , bzw. kurz Last.

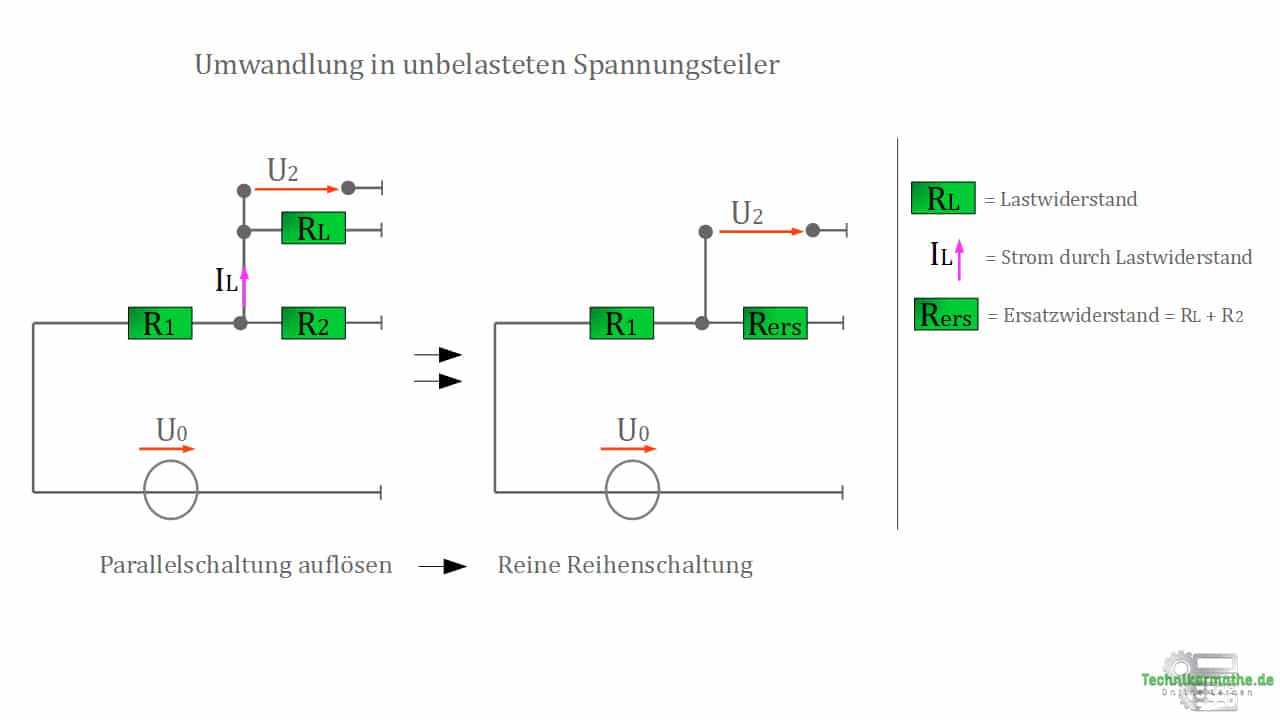
Unbelasteter Spannungsteiler – Vorgehensweise bei der Umwandlung

In der obigen Abbildung kannst du erkennen, dass unser Gesamtstrom am Knoten in zwei Teilströme aufgeteilt wird und diese durch die Widerstände $R_2$ und $R_L$ verlaufen.

Somit können wir unsere bekannte Gleichung zum unbelasteten Spannungsteiler hier vorerst nicht verwenden.

Die Lösung besteht darin, dass wir einfach unsere beiden Widerstände $R_2$ und $R_L$ zu einem einzigen Widerstand $R_{ers}$ zusammenfassen.

$R_{ers} = R_2 || R_L = \frac{R_2 \cdot R_L}{R_2 + R_L}$

Jetzt können wir wieder die bekannte Gleichung zum unbelasteten Spannungsteiler verwenden:

$U_2 = \frac{R_{ers}}{R_1 + R_{ers}} \cdot U_0 = \frac{\frac{R_2 \cdot R_L}{R_2 + R_L}}{R_1 + \frac{R_2 \cdot R_L}{R_2 + R_L}} \cdot U_0$

sowie

$U_2 = \frac{R_2 \cdot R_L}{R_1 \cdot R_2 + (R_1 + R_2) \cdot R_L} \cdot U_0$

Im letzten Schritt können wir nun noch die Gleichung vereinfachen indem wir sie zusammenfassen. Hierzu teilen wir die Gleichung durch $R_L$ im Zähler und Nenner:

$U_2 = \frac{R_2}{R_1 + R2 + \frac{R_1 \cdot R_2}{R_L}} \cdot U_0$

Der letzte Term im Nenner dieser Gleichung besagt, dass die Spannung $U_2$ bei einem endlichen Lastwiderstand $R_L$ immer kleiner als die Spannung $U_2$ beim unbelasteten Spannungsteiler ausfällt.

Merk’s dir!

Tritt eine Belastung bei dieser Schaltung auf, so sinkt dadurch die Ausgangsspannung des Spannungsteilers ab.

Regelübersicht: Unbelasteter und Belasteter Spannungsteiler

Zum Ende diese Abschnittes fassen wir nochmals die Spannungsteiler-Regeln zusammen:

Nachfolgend findest du die vier Regeln, die du dir zur Spannungsteilerregel merken solltest!

1. Sind zwei Widerstände in Reihe geschaltet so teilt sich die Gesamtspannung proportional zu den beiden Widerständen auf.

$\frac{U_1}{U_2} = \frac{R_1}{R_2}$

2. Jede Teilspannung $U_i$ in einer Reihenschaltung verhält sich zur Gesamtspannung $U_{AB}$ wie der entsprechende Teilwiderstand $R_i$ zum Gesamtwiderstand $R_{ges}$ der Reihenschaltung.

$\frac{U_i}{U_{AB}} = \frac{R_i}{R_{ges}}$

3. Liegt ein Spannungsteiler mit zwei Widerständen vor, so ist dieser als Sonderfall zu behandeln.

$U_2 = \frac{R_2}{R_1 + R_2} \cdot U_0$

4. Liegt ein belasteter Spannungsteiler mit zwei Widerständen vor, so handelt es sich dabei ebenfalls um einen Sonderfall.

$U_2 = \frac{ R_2 || R_L}{R_1 + R_2 || R_L} \cdot U_0 = \frac{ R_2}{R_1 + R_2} + \frac{R_1 \cdot R_2}{R_L} \cdot U_0$

Beispielaufgabe: Belasteter Spannungsteiler

Was kommt als Nächstes?

Im nächsten Kurstext stellen wir dir ausführlich die Stromteilerregel vor.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++