Nachdem wir dir bisher nur die Spannungsteilerregel vorgestellt haben, folgt nun die Unterscheidung in den unbelasteten und belasteten Spannungsteiler.
Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema. Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET2-Gleichstromtechnik
Unterscheidung zwischen unbelastetem Spannungsteiler und belastetem Spannungsteiler
Unbelasteter Spannungsteiler
Zuerst erklären wir dir den unbelasteten Teiler.

Grundlagen zum unbelasteten Spannungsteiler
Wir schauen uns jetzt zwei Ausprägungen Teilers an. Die erste Variante ohne und die zweite Variante mit Abgriff.
Variante 1 – ohne Abgriff /Potentiometer
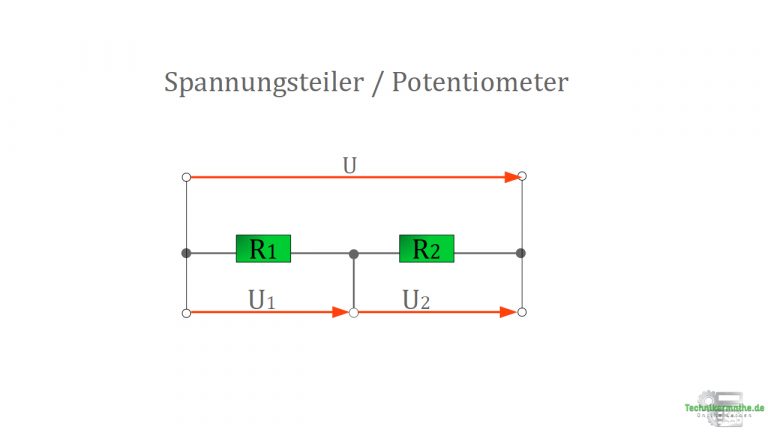
In der nächsten Abbildung sind zwei Widerstände (![]() und
und ![]() ) in Reihe dargestellt.
) in Reihe dargestellt.
Variante 2 – mit Abgriff
Für eine stetige Änderung des Verhältnisses dient die Anordnung im nächsten Bild.
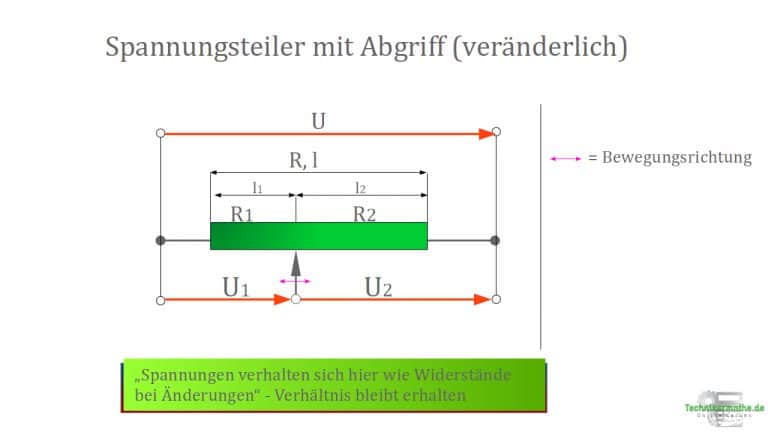
Hier gleitet auf der Widerstandsbahn eines Gesamtwiderstandes ein Kontakt als „Abgriff“ und teilt dabei Gesamtwiderstand in die Teilwiderstände
![]() und
und ![]() auf.
auf.
Die Spannungen verhalten sich hier wie die Widerstände bei Verschiebungen. Das Verhältnis bleibt bei einer Änderung aber konstant.
Weder über den Abgriff noch über den Anschluss zwischen ![]() und
und ![]() fließt ein Strom. Aus diesem Grund bezeichnet man dieses Schaltung als unbelasteten Spannungsteiler.
fließt ein Strom. Aus diesem Grund bezeichnet man dieses Schaltung als unbelasteten Spannungsteiler.
Da in beiden Teilwiderständen der gleich Strom fließt, gilt die
Spannungsteilerregel
Überlegung zum unbelasteten Spannungsteiler
Bisher sind wir immer davon ausgegangen, dass sich bei dem im Bild dargestellten Spannungsteiler die mit dem Gleitkontakt abgegriffenen Teilspannungen linear mit der Kontaktverstellung ändern.
Liegt uns nun ein Widerstand vor, der aus einem kalibrierten Widerstandsdraht besteht, dann kann man für die Widerstände die entsprechenden Längen einsetzen.
So entspricht der Gesamtwiderstand
der Länge
und die Teilwiderstände
![]() und
und ![]() den Teillängen
den Teillängen und
Formal sieht das dann so aus:
Teilwiderstand
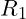
sowie
Teilwiderstand
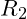
Besonders in der Messtechnik findet der unbelastete Spannungsteiler seine Anwendung. Denn von einer größeren sehr leicht messbaren Spannung kann man sehr genau kleinere nur schwer messbare Spannungen abgreifen. Auch in der Signaltechnik kann ein Spannungsteiler genutzt werden um ein Signal abzuschwächen oder die Lautstärke an einem Audioverstärker zu regeln.
Beispielaufgabe: Spannungsberechnung
Wir suchen den Wert für die Spannung wenn der Widerstand R aus der Abbildung oben durch den Schleifer im Verhältnis
aufgeteilt wird und die Spannung
beträgt.
Nun lösen wir die Aufgabe und nutzen den nachfolgenden Lösungsweg:
Fazit:
- Nicht selten wir zur Beschreibung der Schleiferstellung eine Variable x mit den Bereichen 0 < x < 1 ausgewählt.
sowie
- Dabei ist der untere Teil des Widerstandes
und der obere Teil des Widerstandes
.
sowie
- Beide zusammen stellen den Gesamtwiderstand P des Potentiometers dar.
Die Ausgangsspannung aus unserem Beispiel können wir somit ausdrücken durch:
Nun ist es ja so, dass die Größe x im Bereich zwischen 0 und 1 liegt. Somit kann die Spannung immer nur kleiner als
sein. Sie stellt immer nur einem Teil von
dar.
Im nächsten Kurstext erklären wir dir ausführlich den belasteten Spannungsteiler.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






