(ET2-17) Der Maschensatz / Maschenregel – 2. Kirchhoffsche Regel [Erklärung, Aufgaben, Videos]

Nachdem du bereits den Knotensatz kennengelernt hast, betrachten wir nun als zweites Kirchhoff’sches Gesetz den Maschensatz (Maschenregel).

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET2-Gleichstromtechnik

Maschensatz (Maschenregel) – Grundlagen

Diese zweite Regel von Kirchhoff findest du in der Literatur auch nicht selten unter dem Begriff Maschenregel. Neben dem Ohmschen Gesetz eignen sich die Regeln von Kirchhoff besonders gut um einfache bis mittelkomplizierte Netzwerke zu lösen.

Der Maschensatz nach Kirchhoff ist ein Grundprinzip in der Elektrotechnik, das besagt, dass in einem geschlossenen Stromkreis die Summe der Spannungsabfälle über alle Bauteile (wie Widerstände, Batterien usw.) gleich der Summe der angelegten Spannungen ist. Anders gesagt: Die elektrische Energie, die in den Schaltkreis eingespeist wird, entspricht der Energie, die im Kreis verbraucht wird. Das Gesetz beruht auf der Erhaltung der Energie und wird oft verwendet, um komplexe elektrische Netzwerke zu analysieren.

Merk’s dir!

“Der Maschensatz von Kirchhoff hilft elektrische Spannungen innerhalb einer Masche in einem Gleichstromnetzwerk zu bestimmen.”

Maschensatz (Maschenregel) – Spannungen

Der Maschensatz von Kirchhoff hilft dir elektrische Spannungen innerhalb einer Masche in einem Gleichstromnetzwerk zu bestimmen.

Du hast bereits Maschen in einem vorangegangenen Abschnitt kennengelernt. Jeder geschlossene Stromumlauf gilt als Masche $M$ . Deshalb ist der einfache Grundstromkreis im Grunde auch nichts anderes als eine Masche.

In der nächsten Abbildung siehst du eine Masche.

Die erforderlichen Zählpfeile und der Maschenumlaufsinn sind bereits eingetragen worden.

Allein aus dieser Abbildung kannst du dir als Techniker viel ableiten. Demnach gilt, dass die Summe aller Spannungen innerhalb einer Masche null sein muss. Und dabei ist es egal ob es sich um erzeugte oder verbrauchte Spannungen handelt.

Erzeugte Spannungen treten an den Spannungsquellen auf sowie

verbrauchte Spannungen treten an den Verbrauchern (Widerständen) auf.

Aussage des 2. Kirchhoff’schen Gesetzes (Maschenregel)

Diese Aussage ist nichts anderes als der Maschensatz, bzw. die 2. Kirchhoff’sche Regel.

Nicht vergessen…

Ausgehend von einer Masche gilt, dass die Summe der Energieänderungen aller Spannungsquellen gleich der Summe der Energieänderungen an den Verbrauchern ist.

Das bedeutet zeitgleich, dass die Summe aller umgesetzten Energie dem Wert null entspricht. Fassen wir noch ein mal in Bezug auf Spannungen zusammen. Die Aussage der 2. Kirchhoff’schen Regel ist:

„Bei einem Umlauf entlang der Zweige einer Masche ist die Summe aller Spannungen gleich null. “

Rechnen mit dem Maschensatz (Maschenregel)

Aus mathematischer Sicht können wir eine Formel erstellen, die diesen Gedanke aufgreift:

$\sum_{i =1}^n U_i = 0$

2. Kirchhoffsches Gesetz

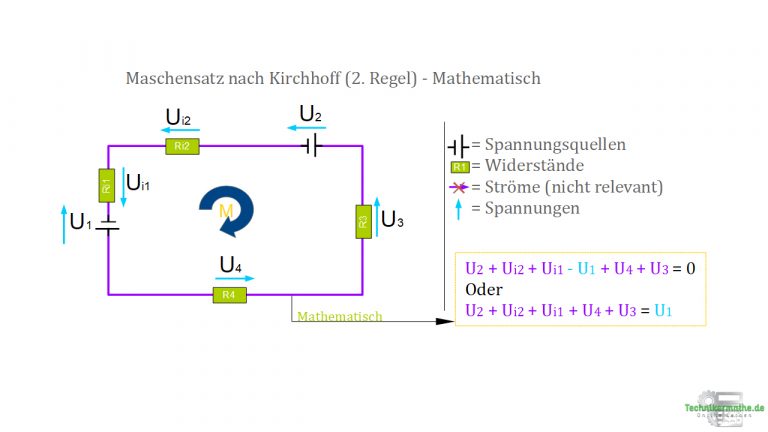
Beziehen wir uns auf unser obiges Beispiel, so sind die Gleichungen für beide Formulierungen:

$U_2 +U_{i2} + U_{i1} - U_1 + U_4 + U_3 = 0$

Falls du einmal eine bestimmte Spannung bei Kenntnis der anderen Spannungen nach dem Maschensatz ermitteln sollst, wie beispielsweise $U_1$ , so reicht es vollkommen aus, wenn du die Gleichung entsprechend nach $U_1$ auflöst.

Dieser Vorgang gelingt dir indem du alle anderen Spannungen auf die andere Seite überführst, so wie nachfolgend geschehen:

$U_2 +U_{i2} + U_{i1} + U_4 + U_3 = U_1$

Fazit zum Maschensatz

Beachte bitte bei Berechnungen auf eine Einheitlichkeit. Alle Spannungen sollten entweder positiv oder negativ in die Berechnungen eingehen. Egal wie du deine Auswahl triffst, denke daran, dass dazu entgegengesetzten Spannungen immer auch das entgegensetzte Vorzeichen erhalten müssen.

In der Abbildung wurden Zählpfeile verwendet, damit für dich direkt und eindeutig klar ist, welche Eigenschaft (zu/ab) eine Spannung aufweist. In vielen Fällen verwendet der Techniker für die Quellenspannung ein positives Vorzeichen und für die anderen Spannungen ein negatives Vorzeichen.

Beispielaufgabe zum 2. Kirchhoff’schen Gesetz (auf Prüfungsniveau)

Jetzt folgt ein ausführliches Beispiel zur Bestimmung von Strömen mit Hilfe des Maschensatzes und unter Anwendung des Substitutionsverfahrens in drei Teilen.

“Du kannst jeden dieser Teile der Lösung sowohl als Videoclip verfolgen oder wenn du lieber liest, dann steht dir dafür die ausführliche Lösung in Textform immer unter dem Video zur Verfügung.”

Beispiel 1: Bestimme die Ströme mit dem Maschensatz.

Dir ist folgendes Netzwerk gegeben:

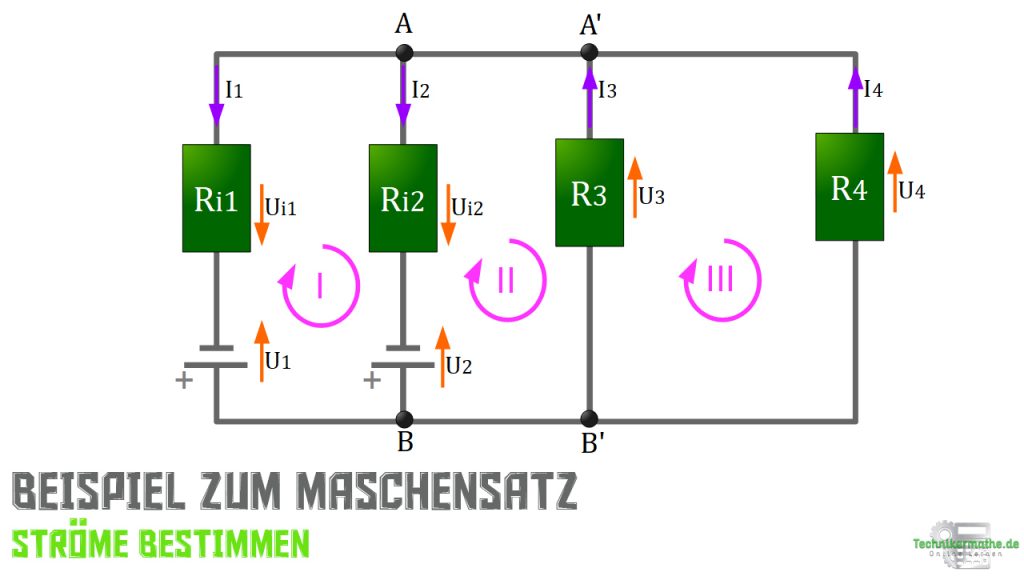
Maschensatz - Beispiel - Netzwerk - Ströme bestimmen — Maschensatz – Beispiel – Netzwerk – Ströme bestimmen

Deine Aufgabe ist es die 4 Ströme $I_1, I_2, I_3$ sowie $I_4$ zu berechnen.

Gegeben sind dir die folgenden Angaben:

$U_1 = 75 V$

$U_2 = 90 V$

$R_{i1} = 2,1 \Omega$

$R_{i2} = 2,8 \Omega$

$R _3 = 140 \Omega$

$R_4 = 120 \Omega$

zum ersten Teil

++ Lösung Teil 1: Videoclip ++

In dieser Box findest du die Lösung zu der gegebenen Aufgabe.

Lösung Teil 1 (Textform)

Sowohl die Zählpfeile der Ströme und auch der Umlaufsinn der Maschen sind in der Abbildung angegeben.

Für die Lösung benötigen wir insgesamt 4 Gleichungen:

(1) Knotenpunkt B: $I_1 + I_2 - I_3 - I_4 = 0$

(2) Masche I: $U_1 - U_{i1} + U_{i2} - U_2 = 0$

(3) Masche II: $U_2 - U_{i2} - U_3 = 0$

(4) Masche III: $U_3 - U_4 = 0$

Damit wir auch mit den richtigen Größen unsere Lösung bewältigen können, verwenden wir das Ohmsche Gesetz und wende es, dort wo es möglich ist, an um die Spannungen als Produkt aus Widerstand und Strom anzugeben:

(1) $I_ 1 + I_2 - I_3 - I_4 = 0$

(2) $- R_{i1}I_1 + R_{i2} = U_2 - U_1$

(3) $-R_{i2}I_2 - R_3I_3 = -U_2$

(4) $R_3I_3 - R_4I_4 = 0$

Ein solches Gleichungssystem mit vier Unbekannten (siehe unseren Onlinekurs MA2) kann man unterschiedlich lösen. Du kannst die Additionsmethode, den Gaußschen Algorithmus, Determinanten oder das Substitutionsverfahren verwenden. Wir entscheiden uns hier für das Substitutionsverfahren.

zum zweiten Teil

++ Lösung Teil 2: Videoclip ++

Im Lösungsteil 2 passen wir unsere Gleichungen so an, dass wir mit Zahlenwerten rechnen können.

In dieser Box findest du die Lösung zu der gegebenen Aufgabe.

Lösung Teil 2 (Textform)

Für das Gleichungssystem verwenden wir folgenden Lösungsweg:

1 – Wir multiplizieren die Gleichung (1) mit $R_{i1}$ und addieren sie mit der Gleichung (2). Als Ergebnis erhalten wir die Gleichung (2′). Die beiden anderen Gleichungen rühren wir nicht an und nehmen sie unverändert mit zum nächsten Rechenschritt:

(1) $R_{i1}I_ 1 + R_{i1}I_2 - R_{i1}I_3 - R_{i1}I_4 = 0$

(2) $- R_{i1}I_1 + R_{i2} = U_2 - U_1$

(2′)

$(R_{i1} + R_{i2})I_2 - R_{i1}I_3 - R_{i1}I_4 = U_2 - U_1$

(3) $-R_{i2}I_2 - R_3I_3 = -U_2$

(4) $R_3I_3 - R_4I_4 = 0$

2 – Jetzt ersetzen wir $I_4$ in der Gleichung (2′) durch $I_3$ ausgehend von Gleichung (4)

(4) $R_3I_3 = R_4I_4$

(4′) $I_4 = \frac{R_3}{R_3}I_3$

Einsetzen von (4′) in (2′) ergibt

(2′) $(R_{i1} + R_{i2})I_2 - R_{i1}I_3 - R_{i1}\frac{R_3}{R_3}I_3 = U_2 - U_1$

(3) $-R_{i2}I_2 - R_3I_3 = -U2$

3 – Jetzt ersetzen wir $I_3$ in der Gleichung (2′) durch $I_2$ ausgehend von Gleichung (3) und lösen diese anschließend nach $I_2$ auf.

$R_3I_3 = U_2 - R_{i2}I_2$

(3′) $I_3 = \frac{U_2}{R_3} - \frac{R_{i2}}{R_3}I_2$

Einsetzen von (3′) in (2′)

(2′) $(R_{i1} + R_{i2})I_2 - \frac{R_{i1}}{R_3}U_2 + \frac{R_{12}R_{i1}}{R_3}I_2 - \frac{R_{i1}}{R_4}U_2 + \frac{R_{i1}R_{i2}}{R_4}I_2 = U_2 - U_1$

Jetzt klammern wir auf der linken Seite $I_2$ aus und klammern zusätzlich $U_2$ aus, um es anschließend auf die rechte Seite der Gleichung zu überführen.

(2′) $I_2 (R_{i1} + R_{i2} + \frac{R_{i1}R_{i2}}{R_3} + \frac{R_{i1}R_{i2}}{R_4}) = U_2 (1 + \frac{R_{i1}}{R_3} + \frac{R_{i1}}{R_4}) - U_1$

zum dritten Teil

++ Lösung Teil 3: Videoclip ++

Jetzt wo unsere Gleichungen angepasst sind, können wir im Lösungsteil 3 damit beginnen die uns gegebenen Zahlenwerte einzusetzen und weiter zusammen zu fassen.

In dieser Box findest du die Lösung zu der gegebenen Aufgabe.

Lösung Teil 3 (Textform)

1- Jetzt setzen wir die Zahlenwerte ein und lösen nach $I_2$ auf.

(2′) $I_2 (2,1 \Omega + 2,8 \Omega + \frac{2,1 \cdot 2,8}{140}\Omega + \frac{2,1 \cdot 2,8}\Omega = 90 V ( 1 + \frac{2,1}{140} + \frac{2,1}{12}) - 75 V$

Jetzt noch weiter zusammenfassen:

(2′) $I_2 (2,1 + 2,8 + 0,042 + 0,049) \Omega = 90 V (1 + 0,015 + 0,0175) - 75 V$

Auflösen nach $I_2$ liefert uns:

$I_2 \cdot 4,99 \Omega = 17,9 V$

$I_2 = \frac{17,9 \Omega}{4,99 V} = 3,59 A$

2 – Als nächstes bestimmen wir den Teilstrom $I_3$ unter Kenntnis von $I_2$ und unter Hinzunahme von Gleichung (3′)

(3′) $I_3 = \frac{U_2}{R_3} - \frac{R_{i2}}{R_3}I_2$

(3′) $I_3 = \frac{90 V}{140 \Omega} - \frac{2,8}{140} \cdot 3,59 A$

Ausrechnen ergibt für $I_3$

$I_3 = 0,644 A - 0,0718 A = 0,5722 \approx 0,57 A$

3- Im vorletzten Schritt bestimmen wir nun den Teilstrom $I_4$ mit der Kenntnis von $I_3$ mit Hilfe von Gleichung (4′)

(4′) $I_4 = \frac{R_3}{R_4}I_3$

(4′) $I_4 = \frac{140}{120} \cdot 0,57 A$

Ausrechnen ergibt für $I_4$

$I_4 = 0,665 A$

4 – Im letzten Schritt berechnen wir nun noch den Teilstrom $I_1$ und nehmen dafür ganz elegant die Gleichung 1 (Knotenpunktgleichung), denn die anderen Ströme kennen wir ja bereits:

(1) $I_1 = I_3 + I_4 - I_2$

(1) $I_1 = 0,57 A + 0,655 A - 3,59 A$

Ausrechnen ergibt für $I_1$

$I_1 = -2,355 A \approx - 2,36 A$

Upsala… Was ist denn das? Der Strom $I_1$ ist negativ? Was bedeutet das? – Es bedeutet, dass er im Schaltplan unseres Netzwerkes falsch eingezeichnet und korrekterweise gespiegelt werden muss.

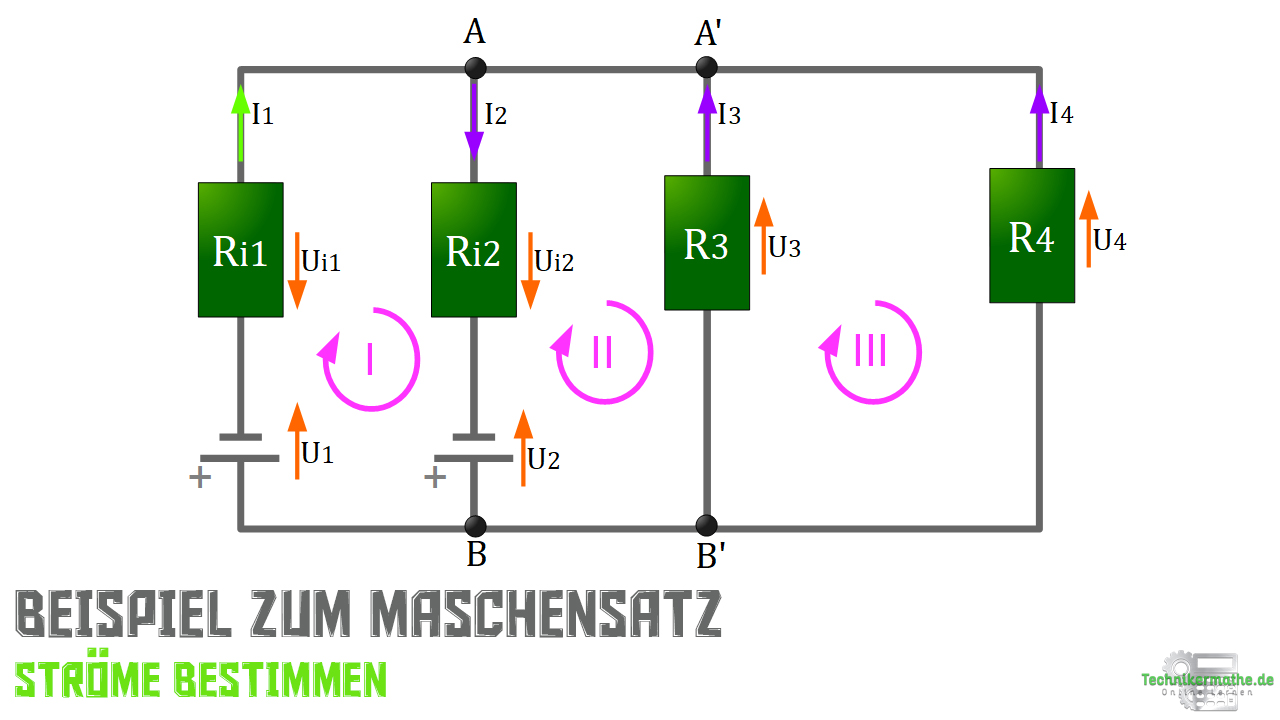
Maschensatz - Schaltplan (korrigiert) — Maschensatz – Schaltplan (korrigiert)

zum vollständigen Video

++ Vollständige Lösung im Gesamtclip ++

Nachfolgend findest du noch mal die drei Clips zusammengefasst in einem Gesamtclip:

Was kommt als Nächstes?

“Nachdem du jetzt den Maschensatz kennengelernt hast, erklären wir dir im nächsten Kurstext ausführlich die Spannungsteilerregel.“

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++