(ET2-07) Gruppenschaltung – Reihen- und Parallelschaltung [Erklärung, Klausuraufgabe, Videoclips]

In diesem Kurstext stellen wir dir die Gruppenschaltung vor und erklären dir die Lösung dieser Schaltungsart ausführlich mit zwei Übungsbeispielen.

Für ein optimales Verständnis hilft dir insgesamt 2 Videoclips und 3 ausführliche Übungsbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET2-Gleichstromtechnik

Gruppenschaltung – Grundlagen

Merk’s dir!

Tritt ein Stromkreis auf, bei dem Widerstände sowohl parallel als auch in Reihe geschaltet sind, spricht der Techniker von einer Gruppenschaltung.

Das kenn ich aber anders…

Obwohl man hin und wieder auch mal den Begriff Gemischte Schaltung für diese Schaltungsart in der Literatur findet.

Wie so ein entsprechender Schaltplan aussehen kann, siehst du in der nächsten Abbildung:

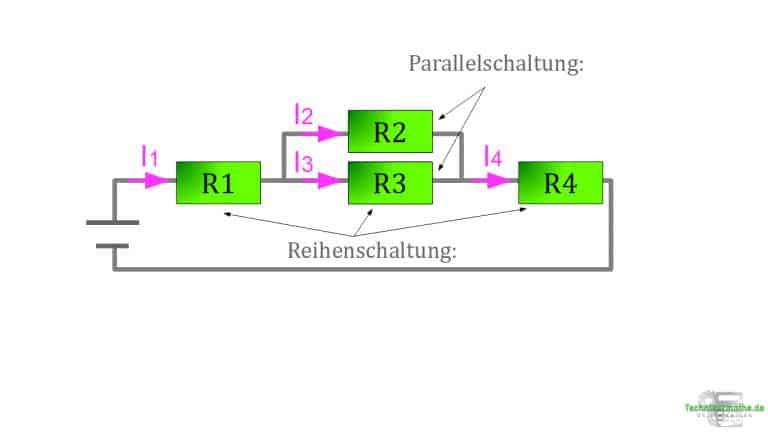
Gemischte Schaltung - Gruppenschaltung — Gemischte Schaltung – Gruppenschaltung

Unterschiede – Reihen- & Parallelschaltung

Bevor wir nun mit der Berechnung beginnen, hier ein paar Unterschiede zwischen einer Reihenschaltung und Parallelschaltung:

Bei einer Reihenschaltung sind alle Widerstände in einer Leitung in Reihe geschaltet.

sowie

Bei einer Parallelschaltung verzweigt sich die Leitung in mehrere Leitungen, in denen einzelne Widerstände liegen.

sowie

Bei einer Reihenschaltung fließt durch jeden Widerstand der gleiche Strom, nur die Spannungen sind je nach Widerstand unterschiedlich.

sowie

Bei einer Parallelschaltung fließt durch jeden Widerstand ein unterschiedlicher Strom. Die Spannung ist an jedem Widerstand gleich.

Merk’s dir!

Liegt eine Kombination wie im obigen Bild vor, dann empfiehlt es sich zuerst die parallel geschalteten Widerstände zusammenzufassen, bevor man anschließend die in Reihe geschalteten Widerstände berechnet.

++ Videoclips – Gruppenschaltung ++

In den folgenden Videos zeigen wir euch Beispiele zur Gruppenschaltung auf.

++ Videoclip 1 – Gruppenschaltung ++

++ Videoclip 2: Gruppenschaltung ++

Beispiele: Gruppenschaltung

Prüfungsbeispiel zur Gruppenschaltung 1

Im nächsten Beispiel stellen wir dir die Berechnung der Gruppenschaltung vor.

Aufgabenstellung - Beispiel 1

undefiniert

Beispiel: Gruppenschaltung

Du möchtest für deine DJ-Lichtanlage mehrere Lampen so schalten, wie es in der Abbildung oben dargestellt ist.

Obwohl du die Angabe der einzelnen Widerstände hast, möchtest aber wissen wie groß der Gesamtwiderstand deiner Schaltung ist.

Gegeben hast du folgende Angaben:

$R_1 = 40 \Omega$

sowie

$R_2 = 30 \Omega$

sowie

$R_3 = 20 \Omega$

sowie

$R_4 = 10 \Omega$

Lösung - Beispiel 1

Wie bereits oben erwähnt, ist es sinnig zuerst die parallel geschalteten Widerstände (R2 | R 3) zusammen zu fassen:

1 – $R_{ges} = R_{23} = \frac{R_2 \cdot R_3}{R_2 + R_3}$

2 – $R_{23} = \frac{ 30 \Omega \cdot 20 \Omega}{30 \Omega + 20 \Omega}$

3 – $R_{23} = \frac{600 \Omega}{50 \Omega}$

4 – $R_{23}= 12 \Omega$

Als Zwischenergebnis erhältst du den Ersatzwiderstand R23 = 12 Ω. Die tiefergestellte 23 drückt aus, dass hier zwei Widerstände (R2 | R3) zusammen gefasst wurden.

Damit ändert sich unser Schaltkreis zu

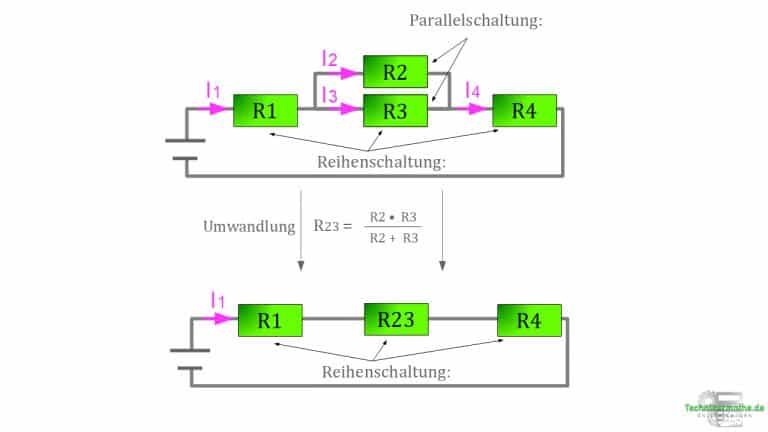
In der neuen Version liegt nur noch eine Reihenschaltung vor, die du ganz einfach ausrechnen kannst indem du die einzelnen Widerstände addierst:

$R_{ges} = R_1 + R_{23} + R_4$

einsetzen:

$R_{ges} = 40 \Omega + 12 \Omega + 10 \Omega$

zusammenfassen:

$R_{ges} = 62 \Omega$

Für den Gesamtwiderstand erhältst du einen Endwert von Rges = 62 Ω.

Prüfungsbeispiel zur Gruppenschaltung 2

Kommen wir nun zu einem etwas schwierigerem Beispiel auf Klausurniveau:

Aufgabenstellung - Beispiel 2

undefiniert

Beispiel: Gruppenschaltung 2

Deine Kollegen und du machen einen bezahlten Betriebsausflug zur Hannovermesse. Dort entdeckt ihr den einsamen Stand eines Elektronik-Herstellers bei dem es etwas zu gewinnen gibt.

Schnell merkt ihr, man nicht einfach ein Rad drehen muss, sondern den Gesamtwiderstand einer Gruppenschaltung berechnen soll, so wie in der Abbildung dargestellt.

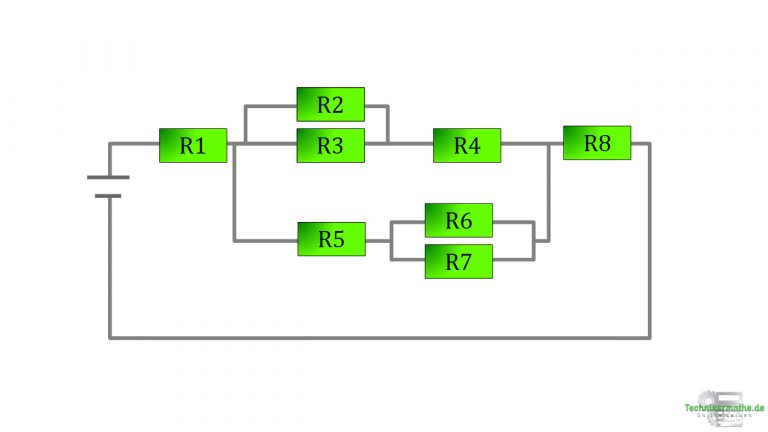
Während deine Kollegen laut lachen, abwinken und sich lieber auf die Suche nach dem einzigen McDonalds auf dem Gelände machen, möchtest du unbedingt den Elektrosportwagen gewinnen. Sobald du damit in der Firma vorfährst, bist du der Held, denkst du dir.

Du machst dich an die Rechnung, den dir liegen folgende Angaben zu den Widerständen vor:

$R_1 = 30 \Omega$

sowie

$R_2 = 40 \Omega$

sowie

$R_3 = 60 \Omega$

sowie

$R_4 = 50 \Omega$

sowie

$R_5 = 20 \Omega$

sowie

$R_6 = 10 \Omega$

sowie

$R_7 = 15 \Omega$

und

$R_8 = 10 \Omega$

Lösung - Beispiel 2 - Teil 1

Als Profi der Elektrotechnik fällt dir auf, dass hier mehrere Parallelschaltungen auftreten, die du im Vorfeld zusammenfassen musst. Im Kopf verschaffst du dir einen ersten Überblick, der wie folgt aussehen könnte:

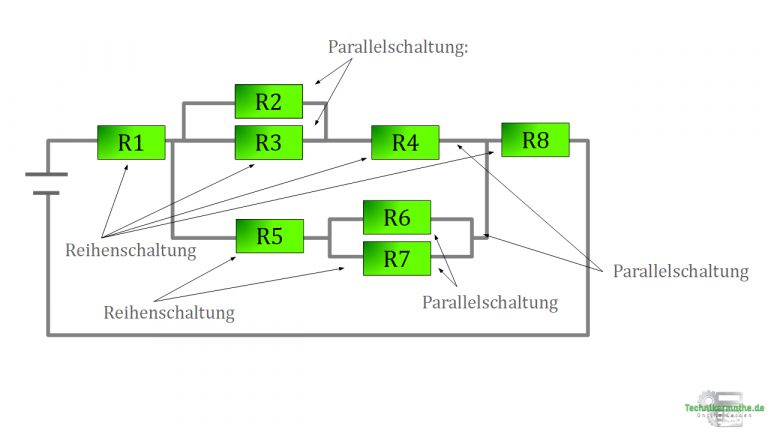
Danach schnappst du dir einen Stift vom Stand sowie eine Serviette vom Hotdog-Brezel-Stand nebenan und fängst an den Schaltkreis abzuzeichnen, bevor du anschließend die Parallelschaltungen markierst, wie hier:

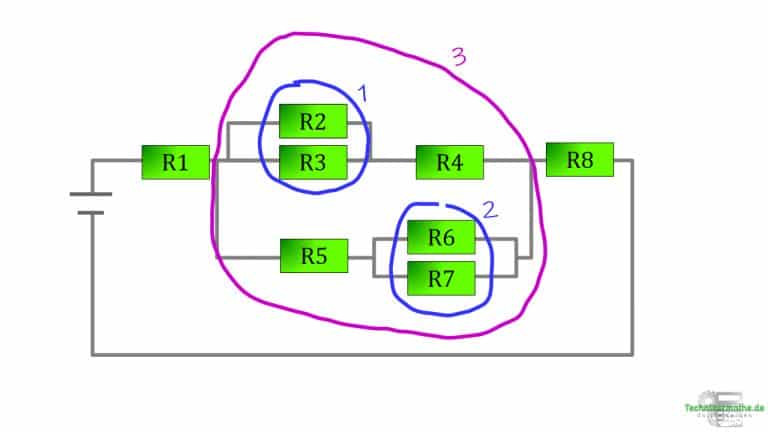
Markieren der parallelgeschalteten Elemente und in Reihe geschalteten Elemente

Lösung - Beispiel 2 - Teil 2

Im ersten Schritt berechnest du die blau eingekreisten, parallelen Widerstände nacheinander und fasst zusammen:

Blau 1

1 – $R_{23} = \frac{R_2 \cdot R_3}{R_2 + R_3}$

2 – $R_{23} = \frac{40 \Omega \cdot 60 \Omega}{ 40 \Omega + 60 \Omega}$

3 – $R_{23} = \frac{2400 \Omega}{100 \Omega}$

4 – $R_{23} = 24 \Omega$

Blau 2

1 – $R_{67} = \frac{R_6 \cdot R_7}{R_6 + R_7}$

2 – $R_{67} = \frac{10 \Omega \cdot 15 \Omega}{ 10 \Omega + 15 \Omega}$

3 – $R_{67} = \frac{150 \Omega}{25 \Omega}$

4 – $R_{67} = 6 \Omega$

Der erste Schritt ist getan und du malst voller Eifer eine neue angepasste Abbildung:

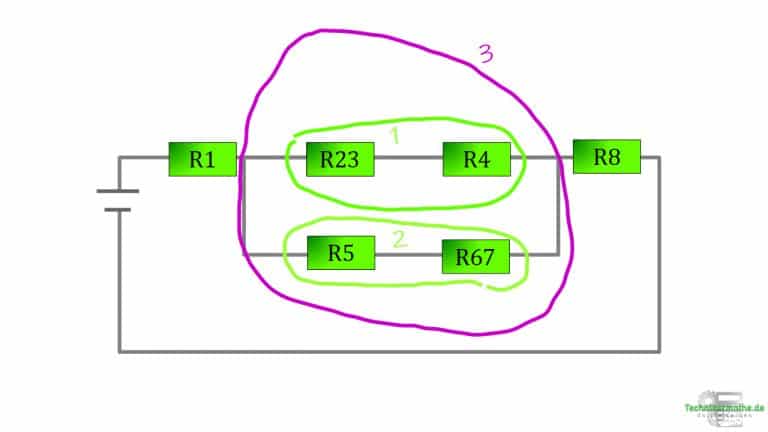
Erneuern der Zeichnung - Vereinfachung des Netzwerks — Erneuern der Zeichnung – Vereinfachung des Netzwerks

Lösung - Beispiel 2 - Teil 3

Nun fällt dir auf, dass es sinnig ist, zuerst die neuen Widerstände in Reihe zusammen zu fassen bevor du die letzte Parallelschaltung auflöst.

Grün 1

1 – $R_{234} = R_{23} + R_{4}$

2 – $R_{234} = 24 \Omega + 50 \Omega$

3 – $R_{234} = 74 \Omega$

Grün 2

1 – $R_{567} = R_{67} + R_{5}$

2 – $R_{567} = 6 \Omega + 20 \Omega$

3 – $R_{567} = 26 \Omega$

Jetzt bleibt nur noch eine Parallelschaltung übrig.

Zwischenzeitlich hat einer deiner Kollegen dir eine Pommes vorbeigebracht. Das passt sehr gut, denn du hast vom ganzen Rechnen Hunger bekommen und der Typ am Hotdog-Brezel-Stand weigert sich komischerweise dir weitere Servietten für deine Berechnung zu geben. Aber zwei Servietten von dem Kollegen – das passt! Denn es ist nur noch wenig zu tun. Zuerst Zeichnung 1:

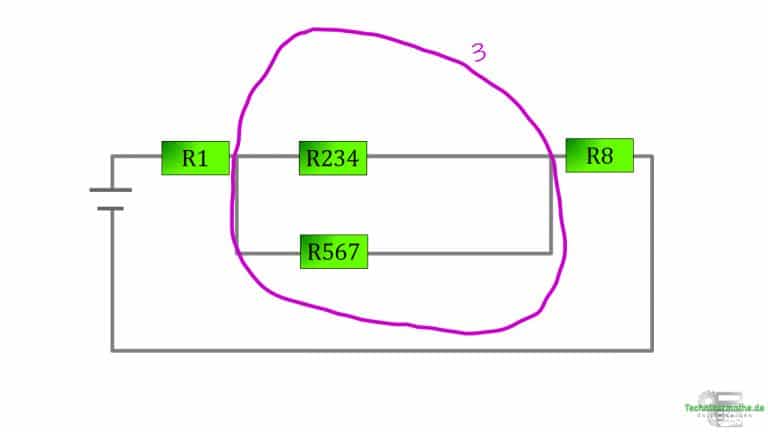
Erneutes Anpassen der Zeichnung - Vereinfachung des Netzwerks — Erneutes Anpassen der Zeichnung – Vereinfachung des Netzwerks

Lösung - Beispiel 2 - Teil 4

Magenta 3

1 – $R_{234567} = \frac{R_{234} \cdot R_{567}}{R_{234} + R_{567}}$

2 – $R_{23} = \frac{74 \Omega \cdot 26 \Omega}{ 74 \Omega + 26 \Omega}$

3 – $R_{23} = \frac{1924 \Omega}{100 \Omega}$

4 – $R_{23} = 19,24 \Omega$

Bäm!! – Denkst du dir, fast geschafft und grinst siegessicher zu dem Hotdog-Brezel-Verkäufer hinüber, der zwar zurückschaut, dir aber nur den Finger neben dem Ringfinger zeigt. Wenn der bloß wüsste, worum es geht.

Egal → Letze Zeichnung, letzte Rechnung – Dann ist es dein Sportwagen.

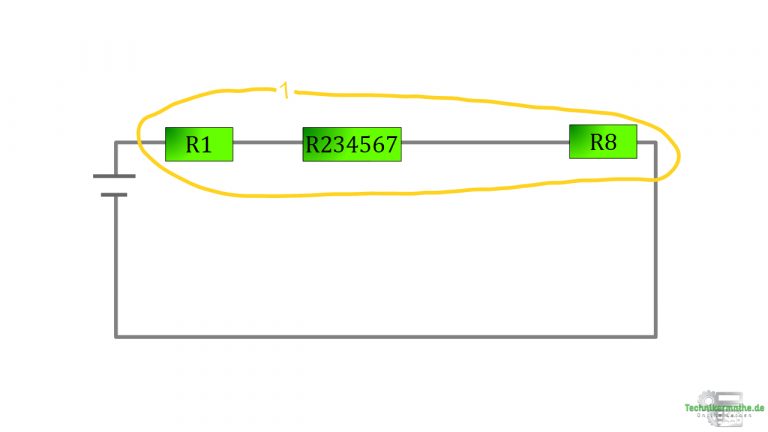
Lösung - Beispiel 2 - Teil 5

Gelb 1:

1 – $R_{12345678} = R_{1} + R_{234567} + R_{8}$

2 – $R_{12345678} = 30 \Omega + 19,24 \Omega +10 \Omega$

3 – $R_{12345678} = R_{ges} = 59,24 \Omega$

Das wars, alles berechnet und du schreibst, nachdem du alles nochmals kontrolliert hast, das Ergebnis auf den Zettel. Danach wirfst ihn in die Losbox.

Ob du den E-Sportwagen nun letztendlich gewonnen hast? Keine Ahnung – Das müsstest du doch besser wissen als wir. Aber check doch einfach deinen Briefkasten.

Was kommt als Nächstes?

Nachdem du nun auch diese Schaltungsvarianten berechnen kannst, erläutern wir dir im nächsten Kurstext die elektrischen Quellen ausführlich und unterscheiden zwischen Spannungsquellen sowie Stromquellen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++