(ET2-06) Die Parallelschaltung von Widerständen [Erklärung, Beispiele, Lernclips]

Nun erfährst du alles Notwendige rund um das Thema Aufbau und Berechnung der Parallelschaltung von Widerständen. Sobald wir die Theorie behandelt haben, folgen drei Übungsbeispiele zu dieser Schaltungsart.

Für ein optimales Verständnis hilft dir insgesamt 2 Videoclips und 3 ausführliche Übungsbeispiele zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET2-Gleichstromtechnik

Die Parallelschaltung von Widerständen – Grundlagen

Merk’s dir!

Wenn du weißt, wie man Reihenschaltungen und Parallelschaltungen (jetziger Kurstext) berechnet, dann bist du auch in der Lage, selbst in komplexen Anordnungen mit vielen Kombinationen von Verbraucher die vorliegenden Teilströme, Teilspannungen und Teilwiderstände zu berechnen.

Aus diesen kannst du dann anschließend auch noch den Gesamtstrom, die Gesamtspannung sowie den Gesamtwiderstand ermitteln.

Merk’s dir!

Eine parallele Schaltung liegt immer dann vor, wenn in einem Stromkreis mehrere Widerstände parallel zueinander geschaltet werden.

Du musst dir das wie eine Gruppe von Läufern in einem Stadion vorstellen, die am Start nebeneinander stehen. Jeder Läufer stellt einen Widerstand dar.

Parallelschaltung von Widerständen mit Gleichungen

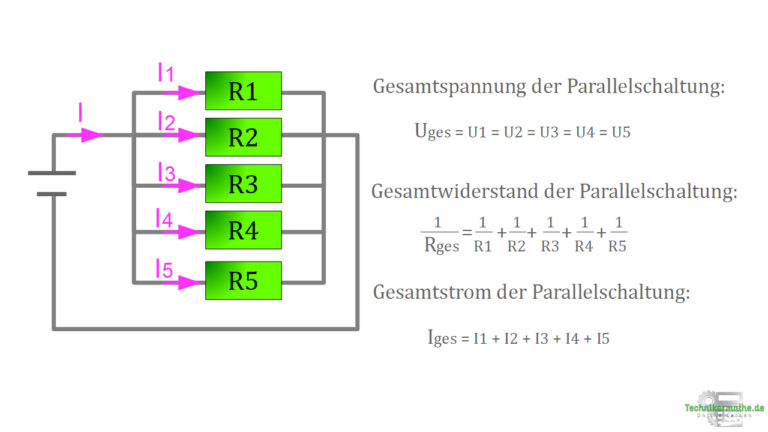
Die Leitung teilt sich auf und in jeder Leitung befindet sich ein Widerstand. Dahinter laufen die Widerstände wieder zusammen. Gäbe es keine Widerstände in den geteilten Leitung wäre ein Kurzschluss die Folge.

Merk’s dir!

Ansonsten bietet die parallele Schaltung den Vorteil, dass der Ausfall eines Verbrauches nicht gleich zu gesamten Zusammenbruch des Stromkreises führt.

Beispiele für parallel geschaltete Elemente

Beispiel: parallel geschaltete Elemente

Bauteile, die im Stromkreis parallel geschaltet werden sind beispielsweise

Lampen,

oder

Spulen,

oder

Kondensatoren,

sowie

Batterien,

Merk’s dir!

Die Spannungen sind bei jedem Teilwiderstand gleich.

Spannungen in der Parallelschaltung – Formel

Anders als bei der Reihenschaltung liegt bei der Parallelschaltung bei jedem Widerstand $R_i$ die gleiche Spannung $U$ an.

$U_{ges} = U_1 = U_2 = U_3 = U_4 = ... = U_n$ Gesamtspannung | Parallelschaltung (Einzelspannungen)

Ströme in der parallelen Schaltung – Formel

Anders als bei der Reihenschaltung ist der Strom bei jedem Widerstand unterschiedlich. Der Gesamtstrom $I_{ges}$ zerlegt sich an den Teilungspunkten in Teilströme $I_i$ , die in Summe wieder den Gesamtstrom darstellen:

$I_{ges} = I_1 + I_2 + I_3 + I_4 + ... + I_n$ Gesamtstrom | Parallelschaltung (Einzelströme)

Widerstände in der Parallelschaltung – Formel

$\frac{1}{R_{ges}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + ... + \frac{1}{R_n}$ Gesamtwiderstand | Parallelschaltung (Einzelwiderstände)

In Summe ergeben die Widerstände dann aber wieder den Gesamtwiderstand.

Welche Gleichungen dir als Ingenieur / Techniker hier zur Verfügung stehen, folgt nun.

Zusammenfassung der Widerstände

Wir unterscheiden jetzt zwei Fälle mit unterschiedlichen Gleichungen:

Fall 1: Zwei parallele Widerstände

Parallelschaltung - Zwei Widerstände — Parallelschaltung – Zwei Widerstände

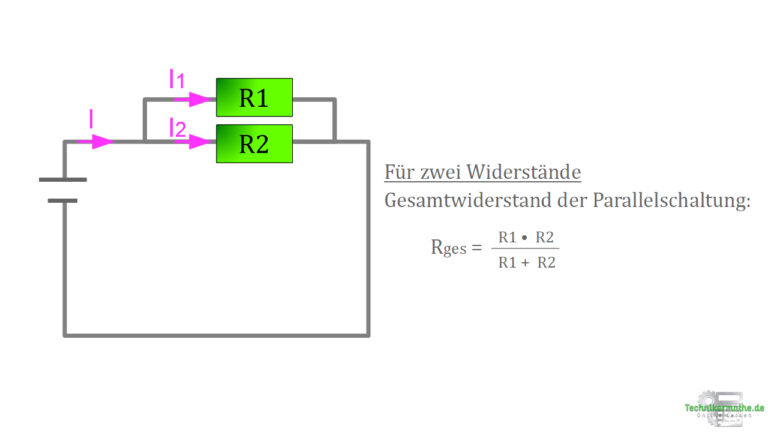
Lägen in der Schaltung im Bild nur zwei parallele Widerstände (R1| R2) vor, so könntest du den Gesamtwiderstand mit folgende Gleichung berechnen:

$R_{ges} = \frac{R_1 \cdot R_2}{R_1 + R_2}$ Gesamtwiderstand | (Zwei Einzelwiderstände)

Fall 2: drei oder mehrere Widerstände

Parallelschaltung - Vier Widerstände — Parallelschaltung – Vier Widerstände

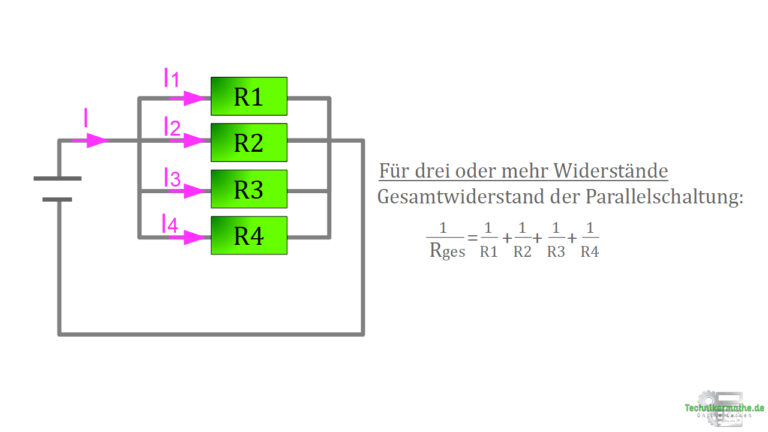
Aber liegen wie in dem Bild nun 4 Widerstände (R1 | R2 | R3 | R4) vor, so kannst du den Gesamtwiderstand mit der nächsten Formel einfach berechnen:

$\frac{1}{R_{ges}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + ... + \frac{1}{R_n}$ Gesamtwiderstand | ( + Drei Einzelwiderstände)

++ Videoclip – Parallelschaltung ++

Im folgenden Video zeigen wir dir ein Berechnungsbeispiel zur parallele Schaltung:

Parallelschaltung – Beispiel

Beispiel: Parallelschaltung von Widerständen

In den nächsten Beispielen stellen wir dir die Berechnung der parallelen Schaltung vor.

Aufgabenstellung 1

Du erhältst von deinem Chef in der Firma den Auftrag eine parallele Schaltung mit zwei Widerständen (Verbrauchern) zu erstellen, weil er damit ein paar Investoren aus Fernost bei der anstehenden Werksbesichtigung beeindrucken möchte.

Parallelschaltung - Beispiel — Parallelschaltung – Beispiel

Bevor du loslegst, möchtest du den Gesamtwiderstand berechnen, denn du kennst lediglich die beiden Einzelwiderstände:

$R_1 = 10 \Omega$

sowie

$R_2 = 40 \Omega$

Lösung

Aber kein Problem für dich, denn bei lediglich 2 Widerständen kannst du folgende Gleichung anwenden:

$R_{ges} = \frac{ R_1 \cdot R_2}{R_1 + R_2} = \frac{ 10 \Omega + 40 \Omega}{ 10 \Omega \cdot 40 \Omega} = \frac{500 \Omega}{50 \Omega} = 10 \Omega$

Das war ja einfach denkst du und übergibst deinem Chef das Ergebnis.

Aufgabenstellung - Beispiel 2

Aufgabenstellung 2

Nachdem dein Chef ist während seiner Frühstückspause in sich gegangen ist und findet er plötzlich heraus, dass er die Investoren damit wohl nicht beeindrucken kann. Er gibt dir den Auftrag die Schaltung auf 4 parallele Widerstände zu erweitern, damit die Investoren nicht mehr aus dem Staunen herauskommen, so zumindest denkt dein Chef.

Beispiel 2 - Parallelschaltung — Beispiel 2

Du verdrehst heimlich die Augen und gehst wieder ans Werk. Gegeben hast du folgende Angaben:

$R_1 = 10 \Omega$

sowie

$R_2 = 40 \Omega$

sowie

$R_3 = 20 \Omega$

sowie

$R_4 = 10 \Omega$

Lösung

Da es sich jetzt um 4 Widerstände (also mehr als 2 Widerstände) handelt, nutzt du die andere Gleichung:

$\frac{1}{R_{ges}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4}$

$\frac{1}{R_{ges}}= \frac{1}{10 \Omega} + \frac{1}{40 \Omega} + \frac{1}{20 \Omega} + \frac{1}{10 \Omega}$

Da du das so nicht gut ausrechnen kannst, bringst du alle Nenner im 1. Schritt auf den gleichen Wert → Gemeinsamer Nenner ist hier 40:

$\frac{1}{R_{ges}} = \frac{4}{40 \Omega} + \frac{1}{40 \Omega} + \frac{2}{40 \Omega} + \frac{4}{40 \Omega}$

Als Zwischenergebnis erhältst du:

$\frac{1}{R_{ges}} = \frac{11}{40 \Omega}$

Nun musst du im nächsten Schritt nach Rges auflösen:

$\frac{1 \cdot 40 \Omega}{R_{ges}} = 11$

dann

$40 \Omega = 11 \cdot R_{ges}$

umstellen

$\frac{40 \Omega}{11}= R_{ges}$

auflösen

$3,6363 \Omega = R_{ges}$

Nun hast du sowohl die Schaltung mit 4 parallelen Widerständen konstruiert und zudem den Gesamtwiderstand berechnet. Alle sind zufrieden und dein Chef lässt sich von den Gästen mega abfeiern. Obwohl du noch immer nicht verstehst, worin sein Beitrag besteht.

Aufgabenstellung 3

Während dein Chef immer mehr Champusflaschen köpft, dabei die Gäste abfüllt und die Musik von Boney M immer lauter wird, ziehst du dich zurück und möchtest zu deiner parallele Schaltung noch die Spannung ausrechnen, zumal du den Gesamtwiderstand Rges und die Stromstärke I der Schaltung kennst:

Beispiel 3 - Parallelschaltung — Beispiel 3

$R_{ges} = 3,6363 \Omega$

$I = 0,18 A$

Lösung

Unter zu Hilfenahme der Ohmschen Gesetzes rechnest du aus:

$U = R_{ges} \cdot I$

dann

$U = 3,6363 \Omega \cdot 0,18 A$

auflösen

$U = 0,654 V$

Sehr wichtig! – Merkregel

Die nachfolgende Regel solltest du dir definitiv merken, denn damit kannst du immer die Richtigkeit deiner Rechnungen nachvollziehen, wenn es um Parallelschaltungen geht:

Merk’s dir!

Bei einer Parallelschaltung gilt immer der Grundsatz, dass der Gesamtwiderstand immer kleiner ist als der kleinste Einzelwiderstand.

Solltest du in einer Berechnung ein anderes Ergebnis erhalten, dann ist deine Berechnung mit sehr hoher Wahrscheinlichkeit nicht korrekt.

++ Videoclip – Parallelschaltung ++

Im nächsten Video findest du noch mal eine Zusammenfassung des Kurstextes sowie des vorherigen Kurstextes und zusätzliche Informationen zur Reihen- und Parallelschaltung.

Reihen- und Parallelschaltung

Was kommt als Nächstes?

Im nächsten Kurstext stellen wir dir ausführlich die Gruppenschaltung vor, als eine Kombination aus Reihen- und Parallelschaltung.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++