(ET2-05) Die Reihenschaltung von Widerständen [Erklärung, Formeln, Beispiele, Lernclips]

In diesem Kurstext erklären wir dir alles Notwendige zum Aufbau und Berechnung der Reihenschaltung für deine Technikerprüfung.

Wenn du weißt, wie man Reihenschaltungen und Parallelschaltungen (kommender Kurstext) berechnet, dann bist du auch in der Lage, selbst in komplexen Anordnungen mit vielen Kombinationen von Verbraucher die vorliegenden Teilströme, Teilspannungen und Teilwiderstände zu berechnen.

Aus diesen kannst du dann anschließend auch noch den Gesamtstrom, die Gesamtspannung sowie den Gesamtwiderstand ermitteln.

Für ein optimales Verständnis helfen dir insgesamt 1 Videoclip und 1 ausführliches Übungsbeispiel zu dem Thema.

Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET2-Gleichstromtechnik

Reihenschaltung - Netzwerk mit Widerständen und Kondensatoren — Reihenschaltung – Netzwerk mit Widerständen und Kondensatoren

Die Reihenschaltung – Grundlagen

Merk’s dir!

Eine Reihenschaltung oder Serienschaltung liegt immer dann vor, wenn in einem Stromkreis mehrere Widerstände hintereinander geschaltet werden.

Du musst dir das wie eine Schlange an der Kasse eines Supermarktes vorstellen. Jeder Kunde stellt einen Widerstand dar.

Wir unterscheiden bei der Reihenschaltung zwischen den Spannungen (Spannungsabfällen) $U_1, U_2, U_3, U_4, U_5$ an den einzelnen Widerständen $R_1, R_2, R_3, R_4, R_5$ sowie der Spannung der Spannungsquelle $U_{ges}$

Einfache Reihenschaltung von Widerständen

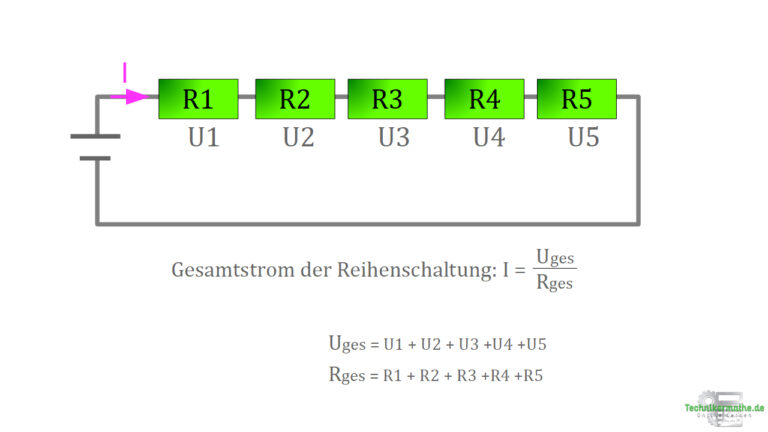
Eine Reihenschaltung in der Elektrotechnik ist eine Anordnung von elektrischen Komponenten, bei der sie hintereinander geschaltet sind, so dass der gleiche Strom durch jede Komponente fließt. In einer Reihenschaltung ist die Gesamtspannung über die einzelnen Komponenten aufgeteilt, wobei die Summe der Spannungen über alle Komponenten gleich der Gesamtspannung der Schaltung ist.

Reihenschaltungen werden häufig verwendet, um die Gesamtspannung zu erhöhen oder zu verringern, indem sie Widerstände oder andere Geräte in Serie schalten. Zum Beispiel werden Glühbirnen in einer Weihnachtslichterkette oft in Reihe geschaltet, so dass sie alle dieselbe Spannung erhalten und gleichmäßig leuchten.

In einer Reihenschaltung beeinflusst der Widerstand jeder Komponente den Gesamtwiderstand der Schaltung, da der Gesamtwiderstand in einer Reihenschaltung die Summe der einzelnen Widerstände ist. Dies bedeutet, dass, wenn eine Komponente in einer Reihenschaltung ausfällt oder unterbrochen wird, die gesamte Schaltung unterbrochen wird und der Strom nicht mehr fließt.

Berechnung des Gesamtstroms – Formel

Der Gesamtstrom kann mit der folgenden Gleichung berechnet werden:

$I = \frac{U_{ges}}{R_{ges}}$ Gesamtstrom (Ohm’sches Gesetz)

Kennzahlen:

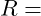$R =$ Elektrischer Widerstand in Ohm (Ω)

sowie

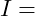$I =$ Elektrische Stromstärke in Ampere (A)

und

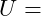$U =$ Elektrische Spannung in Volt (V)

Ströme in der Reihenschaltung – Formel

Durch jeden Widerstand fließt der gleiche Strom I und für jeden Widerstand in dieser Schaltung in Reihe gilt das Ohmsche Gesetz. Bezogen auf die Schlange im Supermarkt könnte man sagen, dass alle Kunden sich im gleichen Tempo vorwärts bewegen.

$I_{ges} = I_1 = I_2 = I_3 = I_4 = ... = I_n$ Gesamtstrom (Einzelströme)

Spannungen in der Reihenschaltung – Formel

Die Spannung U ist unter den einzelnen Widerständen aber nicht gleich. Denn an jedem Widerstand liegt je nach dessen Widerstandshöhe einer Spannungsabfall vor.

In Summe ergeben die Einzelspannung dann wieder die außen am Stromkreis angelegte Gesamtspannung.

$U_{ges} = U_1 + U_2 + U_3 + U_4 + ... + U_n$ Gesamtspannung in der Reihenschaltung (Einzelspannungen)

Widerstände in der Reihenschaltung – Formel

Genauso verhält es sich auch mit den Einzelwiderständen. Diese ergeben in Summe dann den Gesamtwiderstand, bzw. Ersatzwiderstand.

Sind lediglich zwei Widerstände $R_1$ und $R_2$ in Reihe geschaltet, so berechnet sich der Gesamtwiderstand (alternativ: Ersatzwiderstand) $R_{12}$ mit der nachfolgenden Gleichung

$R_{12} = R_1 + R_2$ Gesamtwiderstand zweier Widerstände (Einzelwiderstände)

$R_{ges} = R_1 + R_2 + R_3 + R_4 + ... + R_n$ Gesamtwiderstand in der Reihenschaltung (Einzelwiderstände)

Der Gesamtwiderstand einer Reihenschaltung ist immer größer als der größte Einzelwiderstand. Solltest du auf ein anderes Ergebnis stoßen, dann ist die Berechnung mit sehr hoher Wahrscheinlichkeit nicht korrekt!

Verhältnis von Spannung & Widerstand

Die Berechnung eines Einzelwiderstandes oder einer Teilspannung erfolgt nach dem Ohmschen Gesetz. Folgende Gleichung benötigst du als Techniker:

$I = \frac{U_{ges}}{R_{ges}} = \frac{U_1}{R_1} = \frac{U_2}{R_2} = \frac{U_3}{R_3} = \frac{U_4}{R_4}$

Wir können unseren elektrischen Strom berechnen, wenn wir die Gesamtspannung $U_{ges}$ und den Gesamtwiderstand $R_{ges}$ kennen.

Merk’s dir!

Das Tolle an der Schaltung in Reihe ist, dass wir bereits bei der Kenntnis von einem Teilwiderstand und einer dazugehörigen Teilspannung den Strom I ausrechnen können.

Das bedeutet gleichzeitig, dass am größten Widerstand auch die größte Teilspannung vorliegt. Da der Strom überall gleich groß ist, sorgen ungleiche Widerstände für unterschiedliche Spannungsabfälle an diesen.

++ Videoclip – Reihenschaltung ++

Im folgenden Video zeigen wir dir ein Berechnungsbeispiel zur Reihenschaltung:

Schaltung in Reihe- Beispiel

Beispiel: Reihenschaltung von LEDs

Im nächsten Beispiel stellen wir dir die Berechnung der Schaltung in Reihe vor.

Aufgabenstellung 1

Du möchtest ein neues LED-Lichtpanel für dein Wohnzimmer bauen und die unterschiedlichen LEDS (Widerstände) in Reihe schalten. Außerdem sind dir die Werte für die Widerstände bekannt und du kennst die Spannung. Jetzt möchtest du den Strom bestimmen, der durch dein Panel fließt.

LED-Panel - Reihenschaltung — LED-Panel – Reihenschaltung

$R_1 = 5 \Omega$

$R_2 = 4 \Omega$

$R_3 = 3 \Omega$

$U = 5 V$

Lösung der Beispielaufgabe

Die Lösung erfolgt in 2 Schritten.

1. Gesamtwiderstand bestimmen

2. Ohmsches Gesetz anwenden.

$R_{ges} = R_1 + R_2 + R_3 = 5 \Omega + 4 \Omega + 3 \Omega = 12 \Omega$

$U = R \cdot I \rightarrow I = \frac{U}{R} = \frac{5 V}{12 \Omega} = 0,4166 A$

Im zweiten Schritt möchtest du die Einzelspannungen an den Widerständen bestimmen. Alles was du dafür benötigst hast du bereits vorher gehabt, bzw. dir errechnet.

$R_1 = 5 \Omega$

sowie

$R_2 = 4 \Omega$

sowie

$R_3 = 3 \Omega$

sowie

$I = 0,4166 A$

Für jede Teilspannung wenden wir das Ohm’sche Gesetz an:

1 – Teilspannung 1: $U_1 = R_1 \cdot I = 5 \Omega \cdot 0,4166 = 2,083 V$

sowie

2 – Teilspannung 2: $U_2 = R_2 \cdot I = 4 \Omega \cdot 0,4166 = 1,6664 V$

sowie

3 – Teilspannung 3: $U_3 = R_3 \cdot I = 3 \Omega \cdot 0,4166 = 1,2498 V$

Ob unser Ergebnis stimmt, kannst du ganz einfach überprüfen, indem du die Summe der Einzelspannungen bildest, die der Gesamtspannung U entsprechen muss:

$U = U_1 + U_2 + U_3 = 2,083 V + 1,6664 V + 1,2498 V = 4,9992 V \aproxx U$

Was kommt als Nächstes?

Nachdem du nun die Reihenschaltung kennst, wollen wir dir als nächste Schaltungsart im nächsten Kurstext die Parallelschaltung vorstellen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++