TM2 – Aufgabe: Spannung & Verschiebung im Stab – Temperaturänderung

In dieser Prüfungsaufgabe schauen wir uns an, wie die und die Verschiebung im Stab bestimmt wird, welcher an beiden Enden fest eingespannt ist und eine lineare Temperaturdifferenz erfährt.

In dieser Lerneinheit betrachten wir eine Prüfungsaufgabe zur Bestimmung der Verschiebung im Stab, welcher eine lineare Temperaturänderung erfährt.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Beispiel: Verschiebung im Stab – Lineare Temperaturdifferenz

Aufgabenstellung

Verschiebung, Spannung, Stab, Beispiel, lineare Temperaturdifferenz, Verschiebung im Stab, — Verschiebung, Spannung, Stab, Beispiel, lineare Temperaturdifferenz

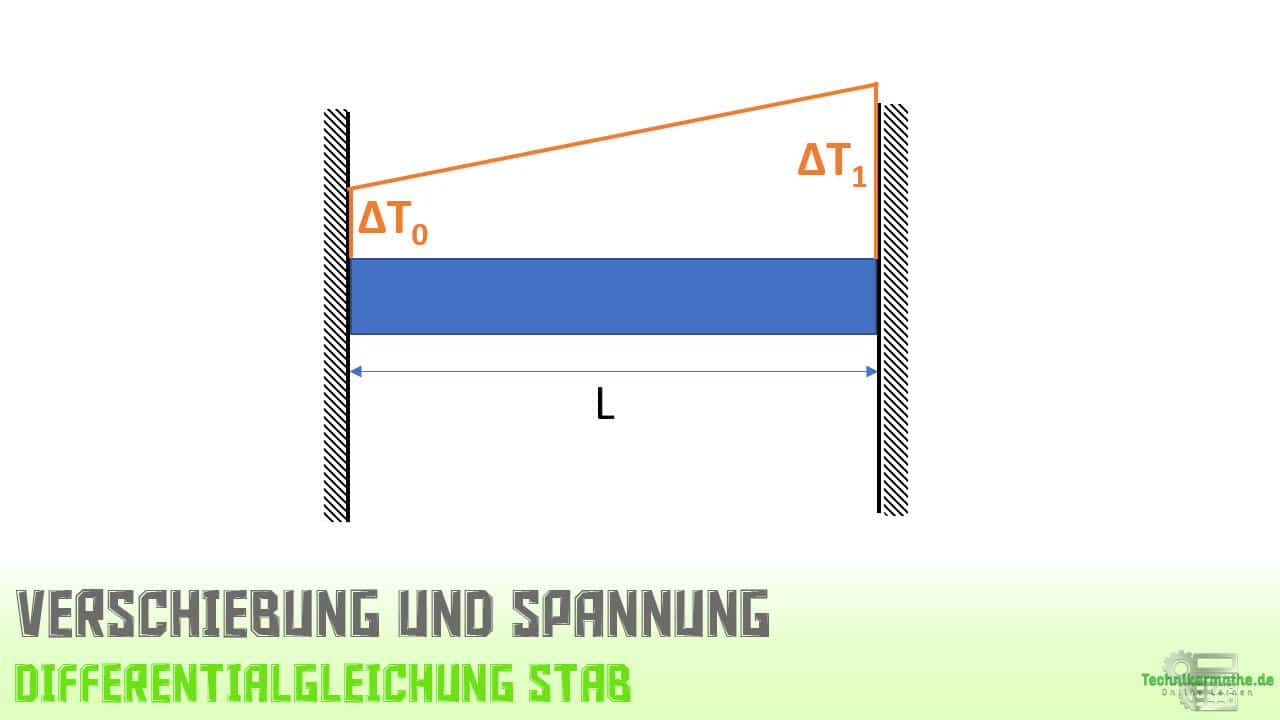
Gegeben sei der obige an beiden Ende fest eingespannte Stab, welcher eine lineare Temperaturdifferenz erfährt. Wir wollen für diesen Stab den Verlauf der Verschiebung sowie den Verlauf der Spannung bestimmen.

Gegeben sind die folgenden Werte:

Längenausdehnungskoeffizient	$\alpha = 23,8 \cdot 10^{-6}$
Elastizitätsmodul	$E = 70.000 \frac{N}{mm^2}$
Temperaturdifferenz ΔT₀	$\triangle T_0 = 10^\circ$
Temperaturdifferenz ΔT₁	$\triangle T_1 = 10^\circ$

Bestimmung der Verschiebung im Stab

Zunächst schauen wir uns an, was wir hier gegeben haben. Wir haben hier einen fest eingespannten Stab gegeben, welcher eine lineare Temperaturdifferenz erfährt. Zur Berechnung können wir die Differentialgleichung der Verschiebung heranziehen:

$EAu'' = -n + (\alpha \cdot \triangle T \cdot EA)'$

Wir haben hier keine Linienlast $n$ gegeben, weshalb n = 0 ist und damit:

$EAu'' = (\alpha \cdot \triangle T \cdot EA)'$

Starten wir nun erstmal damit die Verschiebung u zu bestimmen. Dafür benötigen wir aber die lineare Temperaturdifferenz $\triangle T$ . Am Stabanfang ergibt sich eine Temperaturdifferenz ΔT₀ und diese steigt linear bis zur Temperaturdifferenz am Stabende ΔT₁. Betrachten wir das ganze in einem Koordinatensystem, so erhalten wir die folgende lineare Temperaturdifferenzfunktion:

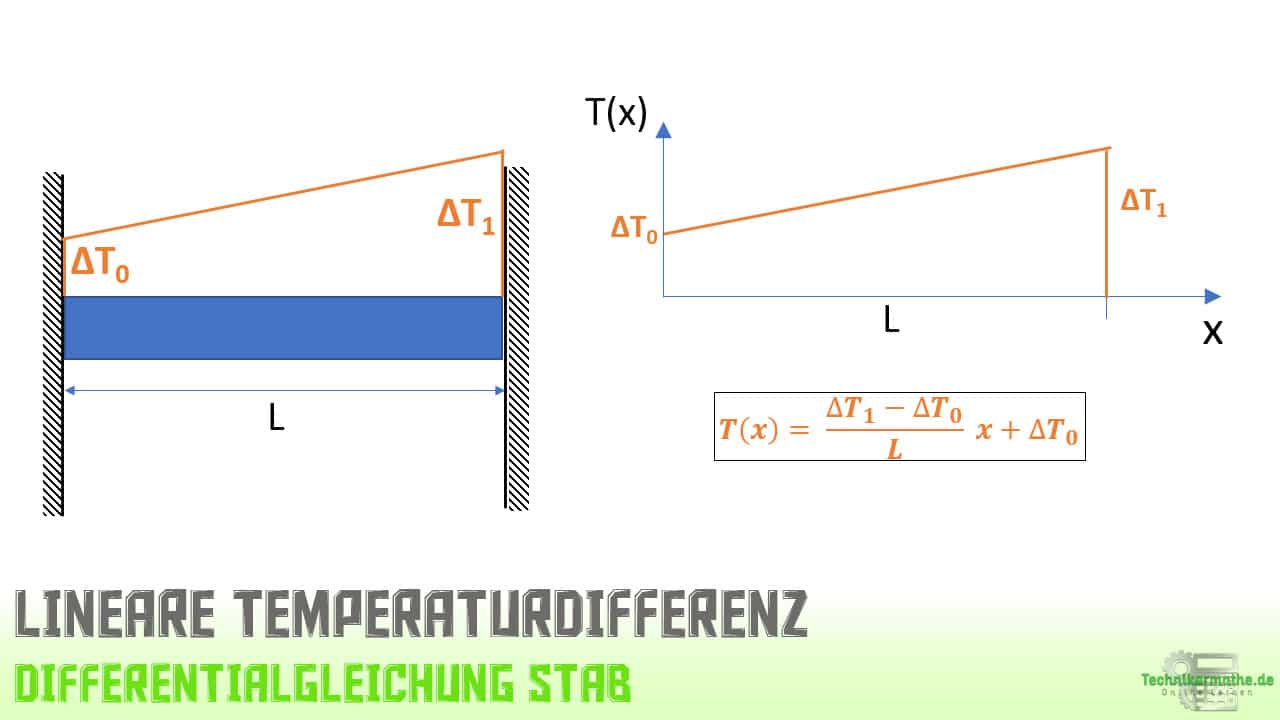
Wärmespannungen, Verschiebung, Spannung, Temperaturänderung, Temperaturdifferenz, eingespannter Stab, Stab, linearer Temperaturverlauf, Verschiebung im Stab — Berechnung des linearen Temperaturverlaufs

Die Temperaturfunktion ergibt sich, indem die Funktionsgleichung einer linearen Funktion herangezogen wird:

Funktionsgleichung einer linearen Funktion

$y = mx + b$

mit

$m$ Steigung

$b$ Schnittpunkt mit der y-Achse

Auf unseren Fall übertragen ist y = ΔT(x). Die Steigung beträgt:

$m = \dfrac{\triangle T_1 - \triangle T_0}{L}$

Der Schnittpunkt mit der y-Achse bzw. T(x)-Achse ist gegeben bei

$b = \triangle T_0$

Wir erhalten somit:

$\triangle T(x) = \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x + \triangle T_0$

Wir können die lineare Temperaturdifferenz nun in die Differentialgleichung der Verschiebung einfügen:

$EAu'' = (\alpha \cdot \triangle T \cdot EA)'$

$EAu'' = (\alpha \cdot (\dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x + \triangle T_0) \cdot EA)'$

Wir können EA rauskürzen und erhalten dann:

$u'' = (\alpha \cdot (\dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x + \triangle T_0))'$

Zunächst bilden wir nun die 1. Ableitung der rechten Seite:

$u'' = \alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L}$

Danach können wir durch zweimaliges Integrieren die Verschiebung u bestimmen.

Merk’s dir!

Wichtig: Wir führen eine unbestimmte Integration durch, d.h. wir müssen Integrationskonstanten berücksichtigen.

Wir starten mit der 1. Integration:

$u' = \int \alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} dx$

I. $u' = \alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x + C_1$

Danach betrachten wir die 2. Integration der Gleichung I:

$u = \int (\alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x + C_1) dx$

II. $u = \alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot \frac{1}{2} x^2 + C_1 \cdot x + C_2$

Wir haben nun mittels zweifacher Integration die Verschiebung u bestimmt. Allerdings müssen wir noch die Integrationskonstanten bestimmen. Diese können wir aus den Randbedingungen (Stabenden) ermitteln.

Die Verschiebung an den Stabenden ist gleich Null, weil der Stab fest eingespannt ist und an den Stabenden damit keine Verschiebung stattfinden kann:

Merk’s dir!

$u(x = 0) = 0$ und $u(x = L) = 0$

Wir betrachten zunächst das rechte Stabende und setzen in die Gleichung II u = 0 für x = 0 ein:

$0 = \alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot \frac{1}{2} 0^2 + C_1 \cdot 0 + C_2$

$C_2 = 0$

Danach betrachten wir das linke Stabende und setzen in die Gleichung II u = 0 für x = L sowie C₂ = 0 ein:

$0 = \alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot \frac{1}{2} L^2 + C_1 \cdot L + 0$

$0 = \alpha \cdot (\triangle T_1 - \triangle T_0) \cdot \frac{1}{2} L + C_1 \cdot L$

$C_1 \cdot L = -\alpha \cdot (\triangle T_1 - \triangle T_0) \cdot \frac{1}{2} L$

$C_1 = -\alpha \cdot (\triangle T_1 - \triangle T_0) \cdot \frac{1}{2}$

Wir haben nun beide Integrationskonstanten bestimmt und können diese als nächstes in die Gleichung II einsetzen:

$u = \alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot \frac{1}{2} x^2 -\alpha \cdot (\triangle T_1 - \triangle T_0) \cdot \frac{1}{2} \cdot x$

Wir haben die Gleichung der Verschiebung bestimmt, können diese aber noch ein wenig zusammenfassen:

$u = \frac{1}{2} \alpha \cdot (\triangle T_1 - \triangle T_0) \cdot x (\frac{x}{L} - 1)$

Wir können nun für eine bestimmte Stelle die Verschiebung im Stab berechnen. Berechnen wir mal die Verschiebung für die beiden Stellen x = 200mm und x = 600mm:

x = 200mm: $u = \frac{1}{2} \cdot 23,8 \cdot 10^{-6} \frac{1}{K} \cdot (50 K - 10 K) \cdot 200mm (\frac{200mm}{1.000mm} - 1) = -0,07616mm$

x = 600mm: $u = \frac{1}{2} \cdot 23,8 \cdot 10^{-6} \frac{1}{K} \cdot (50 K - 10 K) \cdot 600mm (\frac{600mm}{1.000mm} - 1) = -0,114 mm$

Das negative Vorzeichen gibt an, dass hier eine Stauchung stattfindet. Infolge der Temperaturerhöhung im Stab dehnt dieser sich überall aus. Die Ausdehnung wird aber durch die festen Einspannungen an den Stabenden verhindert. Dadurch drücken die Stabquerschnitte gegeneinander und es erfolgt eine Stauchung. Die Stauchung ist in der Mitte bei x = 500mm am Größten (u = -0,119).

Bestimmung der Spannung im Stab

Wir können die Spannung aus der Gesamtspannung bestimmen, da wir in unserem Fall ein eine Gesamtdehnung gegeben haben. Einmal die Wärmedehnung infolge der linearen Temperaturdifferenz und einmal eine Dehnung infolge von Druckkräfte, die durch die feste Einspannung hervorgerufen werden (siehe: Gesamtdehnung und Gesamtspannung):

$\sigma = (\epsilon_{ges} - \alpha \cdot \triangle T) \cdot E$

Die Dehnung haben wir nicht gegeben, wir wissen aber, dass die Dehnung nichts anderes als die Ableitung der Verschiebung ist:

$\dfrac{du}{dx} = u' = \epsilon$

Damit ergibt sich die Spannung bei Gesamtdehnung zu:

$\sigma = (u' - \alpha \cdot \triangle T) \cdot E$

Die Temperaturdifferenz hatten wir bestimmt zu:

$\triangle T(x) = \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x + \triangle T_0$

Einsetzen in die Spannung bei Gesamtdehnung:

(1) $\sigma = (u' - \alpha \cdot [\dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x + \triangle T_0]) \cdot E$

Die erste Ableitung der Verschiebung u’ haben wir mit der Gleichung I weiter oben bestimmt:

I. $u' = \alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x + C_1$

Einsetzen der Integrationskonstante:

$C_1 = -\alpha \cdot (\triangle T_1 - \triangle T_0) \cdot \frac{1}{2}$

Und wir erhalten:

$u' = \alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x -\alpha \cdot (\triangle T_1 - \triangle T_0) \cdot \frac{1}{2}$

Einsetzen in die Spannungsgleichung (1):

$\sigma = (\alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x -\alpha \cdot (\triangle T_1 - \triangle T_0) \cdot \frac{1}{2} - \alpha \cdot [\dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x + \triangle T_0]) \cdot E$

$\sigma = (\alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x -\alpha \cdot (\triangle T_1 - \triangle T_0) \cdot \frac{1}{2} - \alpha \cdot \dfrac{\triangle T_1 - \triangle T_0}{L} \cdot x - \alpha \cdot \triangle T_0) \cdot E$

Die Terme mit x verrechnen sich miteinander zu Null und fallen damit raus:

$\sigma = (-\alpha \cdot (\triangle T_1 - \triangle T_0) \cdot \frac{1}{2} - \alpha \cdot \triangle T_0) \cdot E$

Auflösen der inneren Klammer:

$\sigma = (-\frac{1}{2} \alpha \cdot \triangle T_1 + \frac{1}{2} \alpha \cdot \triangle T_0 - \alpha \cdot \triangle T_0) \cdot E$

Zusammenfassen der Gleichung:

$\sigma = (-\frac{1}{2} \alpha \cdot \triangle T_1 - \frac{1}{2} \alpha \cdot \triangle T_0 ) \cdot E$

$\sigma = -\frac{1}{2} \alpha \cdot (\triangle T_1 - \triangle T_0 ) \cdot E$

Wir haben den Verlauf der Spannung ermittelt. Hierbei handelt es sich um einen konstanten Spannungsverlauf, d.h. die Spannung ist in jedem Punkt im Stab gleich und beträgt:

$\sigma = -\frac{1}{2} \cdot 23,8 \cdot 10^{-6} \cdot (50K - 10K ) \cdot 70.000 \frac{N}{mm^2} = -33,32 \frac{N}{mm^2}$

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++