Wir zeigen dir in dieser Lerneinheit Aufgaben zur Resultierenden. Wir schauen uns an, wie du den Betrag und die Richtung der Resultierenden aus mehreren Kräften berechnest. Dabei betrachten wir ein zentrales Kräftesystem.
Für ein optimales Verständnis helfen dir 5 Aufgaben inklusiver ausführlicher Lösung.
Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH2-Einführung in die Statik.
Aufgaben Resultierende aus mehreren Kräften
Wir schauen uns im nachfolgenden einige Aufgaben zur Berechnung der Resultierenden aus mehreren Kräften an.
In den ersten beiden Aufgaben lernst du erstmal die Teilresultierenden zu berechnen, um dann in den folgenden beiden Aufgaben aus den Teilresultierenden den Betrag und die Richtung der Resultierenden zu bestimmen. In der letzten Aufgabe führst du dann die komplette Berechnung durch, so wie es auch in der Prüfung gefordert wurde.
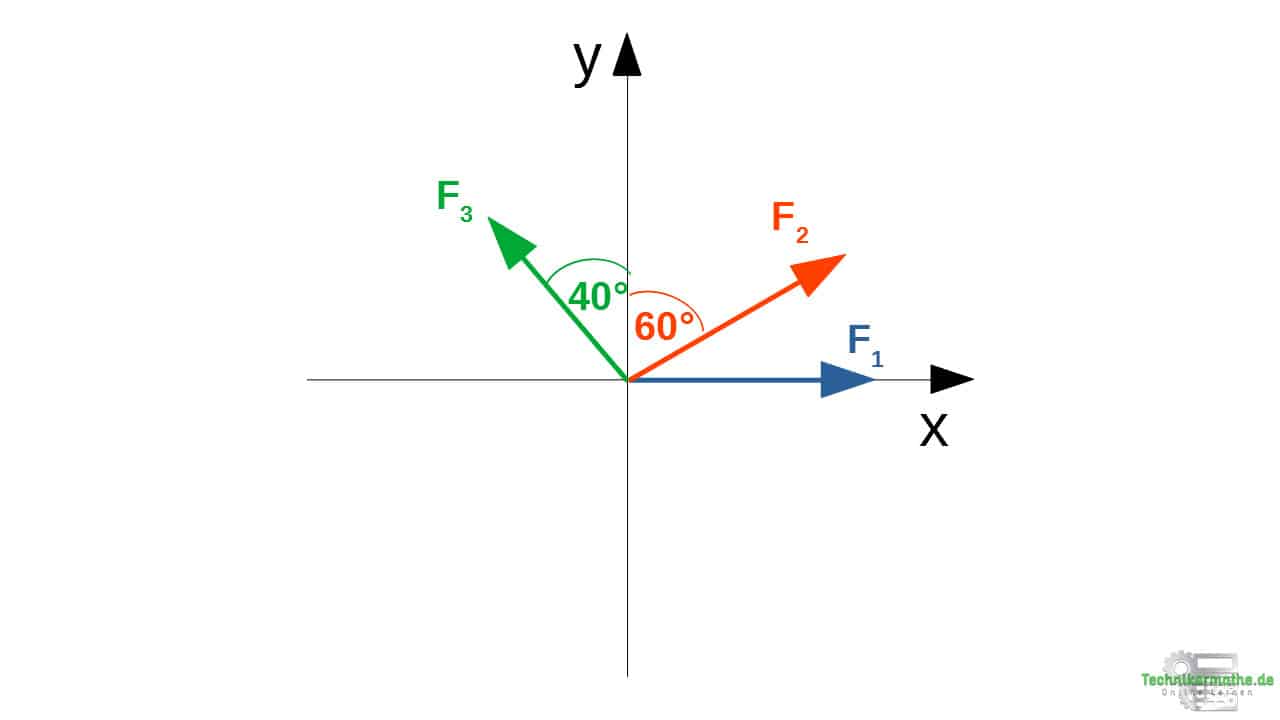
Aufgabe 1: Teilresultierende
1.Schritt: Winkel zur positiven x-Achse bestimmen
2. Schritt: Kräfte in ihre Komponenten zerlegen
In x-Richtung mittels Kosinus:
In y-Richtung mittels Sinus:
3. Schritt: Teilresultierende bestimmen
Die Teilresultierenden bestimmst du, indem du die obigen Komponenten summierst. Für die Teilresultierende in x-Richtung summierst du die Komponenten in x-Richtung, für die Teilresultierende in y-Richtung summierst du die Komponenten in y-Richtung. Achte dabei auf die Vorzeichen!
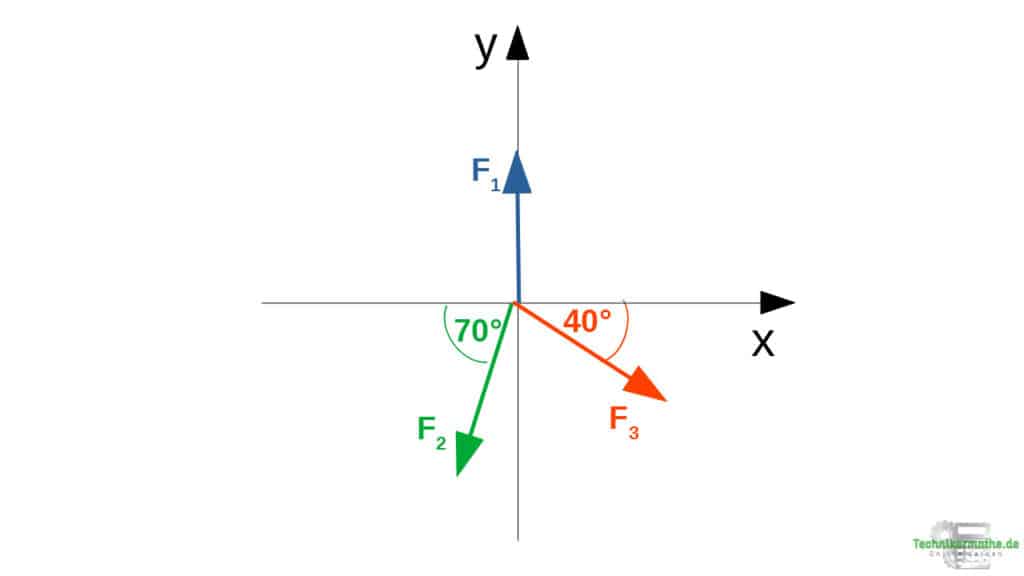
Aufgabe 2: Teilresultierende
1.Schritt: Die Winkel zur positiven x-Achse
2. Schritt: Komponenten mittels Kosinus und Sinus berechnen
Rx mit Kosinus und Winkel zur positiven x-Achse:
Ry mit Sinus und Winkel zur positiven x-Achse:
3. Schritt: Berechnung der Teilresultierenden
Summation der Komponenten in x-Richtung (Vorzeichen beachten):
Summation der Komponenten in y-Richtung (Vorzeichen beachten):
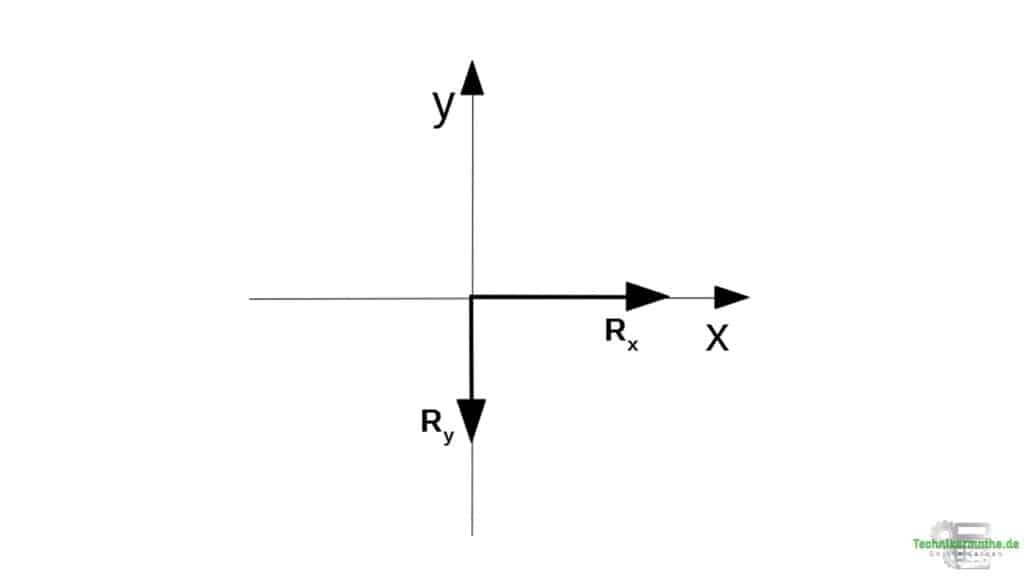
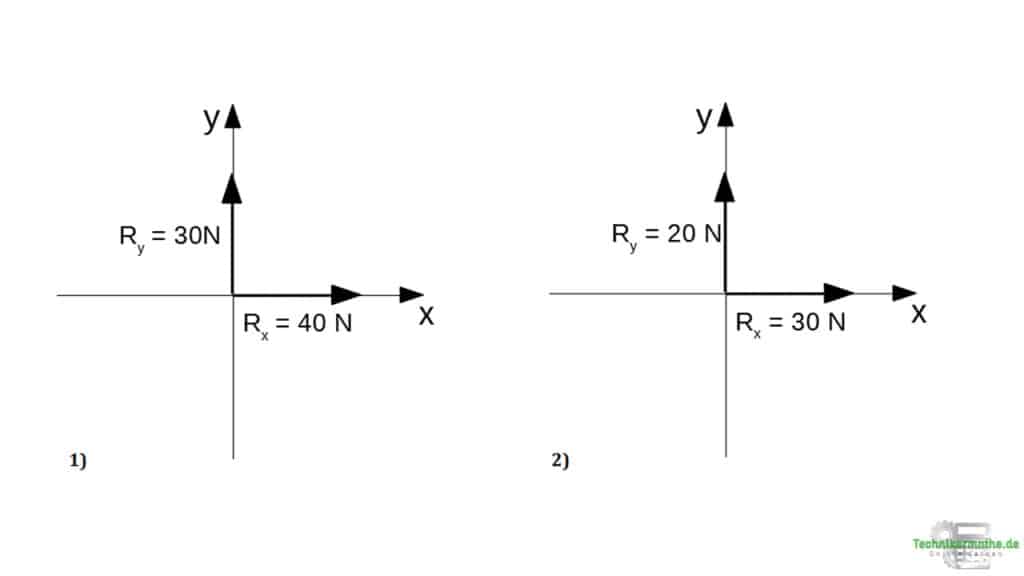
Aufgabe 3: Resultierende (Betrag)
Die Resultierenden kann aus den Teilresultierenden mittels Satz des Pythagoras berechnet werden:
Die Resultierende gehört zu der Grafik 1).
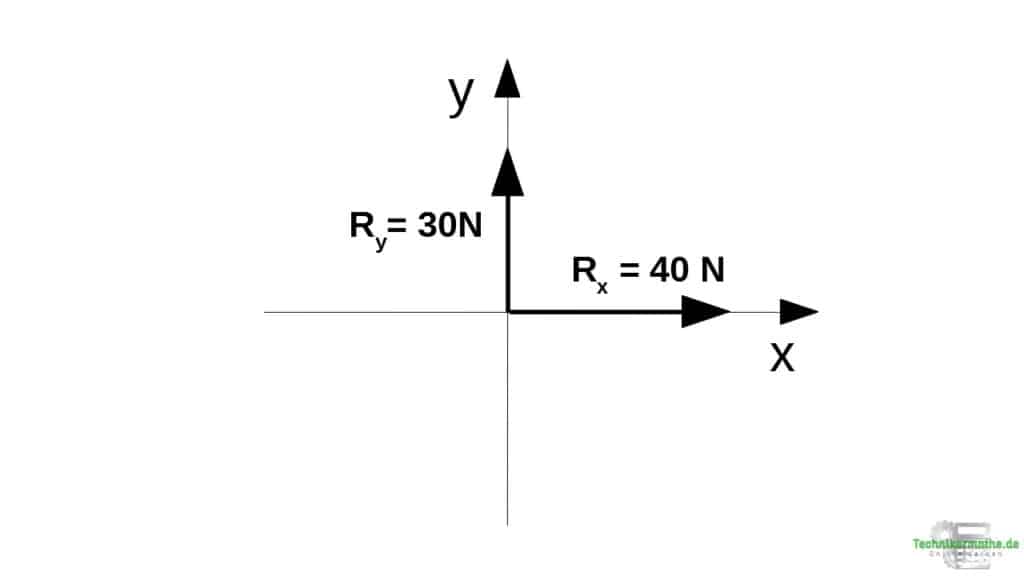
Aufgabe 4: Resultierende (Betrag + Richtung)
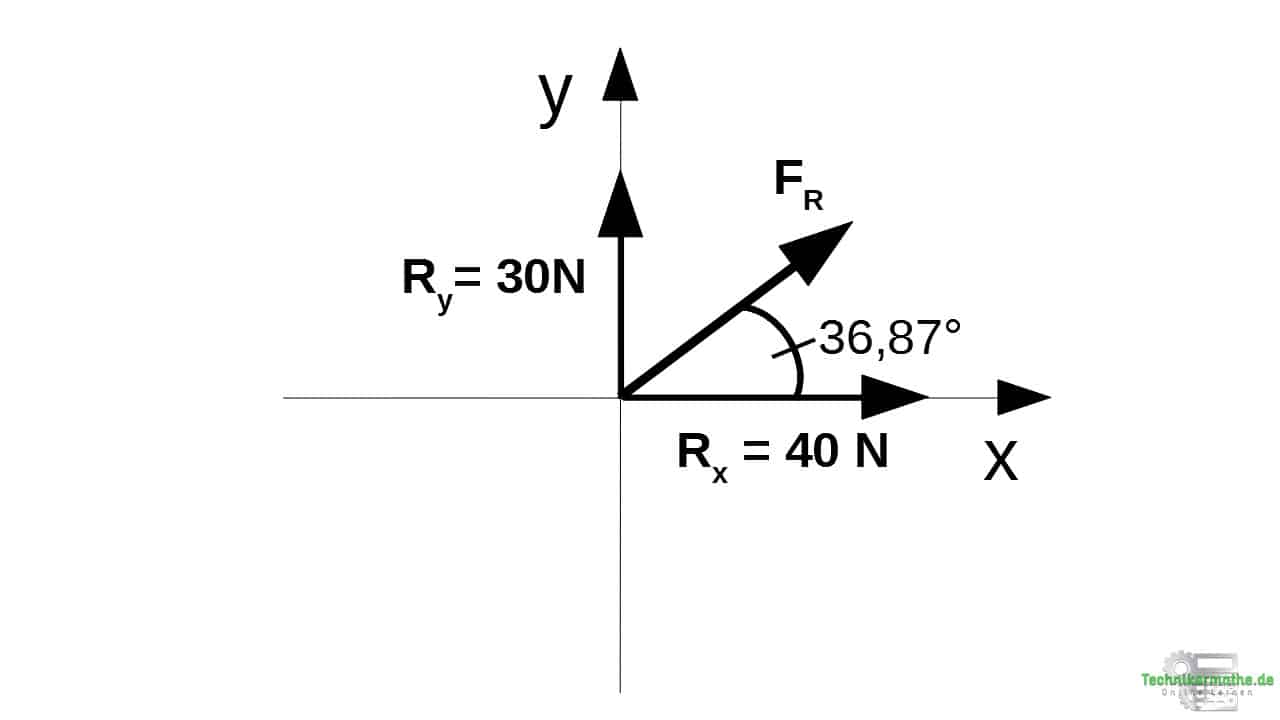
Den Betrag der Resultierenden berechnen wir aus den Teilresultierenden mittels Satz des Pythagoras:
Für die Richtung der Resultierenden berechnen wir immer zunächst den Winkel von der Resultierenden zur Teilresultierenden Rx mittels Tangens:
Auflösen nach dem Winkel mittels Arkustangens (
):
Der Winkel von der Resultierenden zur Teilresultierenden
ist gleich dem Winkel zur positiven x-Achse:
Grund dafür ist, dass die Resultierende im 1. Quadranten des Koordinatensystems liegt. Der Winkel zu Rx ist damit der Winkel zur positiven x-Achse.
Aufgabe 5: Resultierende (Betrag + Richtung)
In dieser Aufgabe sollst du den Betrag und die Richtung der Resultierenden aus den gegeben drei Kräfte berechnen. Dazu kannst du dich an den folgenden Schritten orientieren:
1. Schritt: Winkel von der positiven x-Achse zu den Kräften bestimmen
2. Schritt: Kräfte in x-Komponente mittels Kosinus und y-Komponente mittels Sinus zerlegen
3. Schritt: Teilresultierende und
berechnen (Summation der Komponenten, Vorzeichen beachten)
4. Schritt: Betrag der Resultierende aus den Teilresultierenden mittels Satz des Pythagoras bestimmen
5. Schritt: Richtung der Resultierenden (=Winkel) aus den Teilresultierenden mittels Tangens bestimmen.
1. Schritt: Winkel von der positiven x-Achse zu den Kräften
2. Schritt: Kräfte in ihre Komponenten zerlegen
In x-Richtung mittels Kosinus:
In y-Richtung mittels Sinus:
3. Schritt: Teilresultierende bestimmen (Summen bilden)
Da beide Teilresultierenden positiv sind, zeigen diese in positive Achsenrichtung. Die Resultierende liegt also im 1. Quadranten.
4. Schritt: Betrag der Resultierende bestimmen (Satz des Pythagoras)
5.Schritt: Richtung der Resultierenden bestimmen (Tangens)
Auflösen nach :
Winkel von
zu
Einsetzen:
Da die Resultierende im 1. Quadranten liegt, ist dies auch gleichzeitig der Winkel zur positiven x-Achse.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team