Zudem erklären wir dir was der Spannungsintensitätsfaktor, die Bruchzähigkeit und typische bruchmechanische Kennwerte von Werkstoffen sind.
Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.Mehr zu diesem Thema und der Werkstoffprüfung findest du im Kurs: WT3-Prüfung von Werkstoffen
Risszähigkeit – Definition
“Die Risszähigkeit eines Materials ist ein Maß für die Leichtigkeit mit der sich Risse in diesem Material bilden und vergrößern”

Videoclip: Kompakt-Zugversuch – Überblick
“In diesem Videoclip erhältst du einen ausführlichen Überblick. Zur Vertiefung dienen die nachfolgenden Kurstexte!”
Kompakt-Zugversuch (Risszähigkeitsversuch) – Motivation
Innerhalb der Bruchmechanik untersucht man die Auswirkungen von Rissen an Bauteilen. Das Ziel ist einen solide, mit mathematischen Werten untermauerte Einschätzung zur Rissausbreitung und dem wahrscheinlichen Zeitpunkt des anschließenden Bruchs zu liefern.
“Der Untersuchungsbereich ist das Risspitzennahfeld, also der Bereich, welcher den Riss umschließt und die plastische Zone (Bereich direkt an der Rissspitze).”
Darüber hinaus soll somit die Aussagesicherheit der klassischen Festigkeitsrechnung in einem Konstruktionsprozess maßgeblich erhöht werden.
Denn das Auftreten eines Risses und anschließenden Bruchs an einem technischen Bauteilen wie
- Brücken,
- Schiffsrümpfen,
- Turbinen (GuD),
- Druckkesseln und
- Kraftwerkskomponenten
Diese Bereiche sind immer mit der Gefahr eines spontanen Versagens dieser Komponente verknüpft. Dabei kann im ungünstigsten Fall der Verlust von Menschenleben die Folge sein.
Prüfverfahren wie der Kompakt-Zugversuch untersuchen daher die Eigenschaften und das Verhalten von fehlerbehafteten Werkstücken. Dafür benötigt der Werkstoffprüfer jedoch ein gutes Verständnis für die Zusammenhänge der Bruchmechanik.
Bis heute ist es üblich, bei der Auslegung von Passagierflugzeugen kleine Risse als hinnehmbares Risiko für den Betrieb zu akzeptieren. Das bedeutet, dass im Vorfeld durch Techniker, Ingenieure und Konstrukteure ausgerechnet wird, wie lange ein Kleinstriss an einem Flügel verbleiben darf bis es zu einem möglichen Versagen des Flügels kommen könnte. Man spricht hier von einem kontrollierten Schaden.

“Aus diesem Grund ist besonders das “Wann” ein wichtiges Fragewort in der Bruchmechanik.”
Bruchmechanik – Definition
Die Bruchmechanik untersucht das Versagen von Bauteilen, die einen Riss aufweisen. Dabei untersucht man das Auftreten von Rissen und deren Ausbreitungen unter statischen sowie dynamischen Beanspruchungen bis zum Eintritt des Bruchs.
Die Bruchmechanik ist Teil der Werkstofftechnik, der Elastostatik sowie der Plastomechanik.
Stell dir vor du steht an einer Fertigungsmaschine. Diese Maschine ist starken mechanischen Belastungen ausgesetzt und an einer Stelle hat sich ein Riss gebildet.
Die Bruchmechanik geht jetzt der Frage nach ob das Maschinenteil noch gänzlich intakt ist, oder ob ein Austausch des betroffenen Bauteils notwendig wird.
Konzepte der Bruchmechanik
Über die Jahre haben sich unterschiedliche Konzepte entwickelt, die sich mit diesem Teilbereich der Werkstofftechnik befassen.
- Die linear-elastische Bruchmechanik (LEBM) befasst sich mit der Rissentwicklung bei spröden Werkstoffen. Das bekannteste Konzept ist hier das K-Konzept. Bei diesem Konzept wird der Spannungsintensitätsfaktor
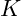 z.B. mit dem Kompakt-Zugversuch ermittelt.
z.B. mit dem Kompakt-Zugversuch ermittelt. - Die Fließbruchmechanik (FBM) untersucht die Rissentwicklung bei duktilen Werkstoffen. Hier haben sich mit dem CTOD-Konzept (Crack Tip Opening Displacement) und dem J-Integral-Konzept (Das J- Integral ist das Linienintegral mit geschlossenem Integrationsweg um die Rissspitze) zwei Konzepte herauskristallisiert.
Fragestellungen der Bruchmechanik
In der Bruchmechanik werden Fragen auf unterschiedliche Anforderungen beantwortet.
- Unter welchen Bedingungen versagt ein Bauteil?
- Welcher Werkstoff eignet sich für meine Konstruktion?
- Wie steht es um die Lebensdauer meines Bauteils bei einer schwingenden Beanspruchung?
- Wie oft muss mein Bauteil auf mögliche Risse inspiziert werden?
- Welche Sicherheiten müssen gegen Bruch ermittelt werden?
- Mit welchen konstruktiven Maßnahmen kann die Bruchgefahr minimiert werden?
- Wir könnte der Rissweg aussehen.
Schädigungsmechanik- Definition
Die Schädigungsmechanik ist Teil der Kontinuummechanik und gibt uns Auskunft über die Materialeigenschaften einer Werkstoffstruktur, die sich durch eine Schädigung am Werkstoff verändert hat.
- Anders als bei der Bruchmechanik bei der die im Makrobereich auftretenden Risse beschrieben werden, ermittelt die Schädigungsmechanik, die im Mikrobereich ablaufenden Schädigungsvorgänge.”
- Ähnlich wie in der Bruchmechanik ist so eine Aussage für Technische Konstruktionen hinsichtlich Tragfähigkeit und Lebensdauer möglich.
Kurz gesagt: “Innerhalb der Schädigungsmechanik wird die Entstehung und Ausbreitung von Mikrorissen untersucht.”
“Mikrorisse sind Kleinstrisse mit einer maximalen Gesamtlänge von 1 mm.”
Als Maß für die Werkstoffschädigung kann dabei das entsprechende Hohlraumvolumen angesehen werden. Dieses Hohlraumvolumen entspricht exakt dem Gesamtvolumen aller Risse.
Übergang von Schädigungsmechanik zu Bruchmechanik
Wenn eine Maschinenbauteil durch eine äußere Kraft beansprucht wird, so führt das zur Bildung von Mikrohohlräumen und –rissen, die sich im Verlauf der Beanspruchung vergrößern. Mit zunehmender Vergrößerung wachsen diese zu größeren Mikroholräumen zusammen.
Zudem können sich in Bereichen mit starken Spannungskonzentration neue Mikrohohlräume bilden. Diese entstehen besonders oft an Einschlüssen.
Diese fortschreitende Strukturschädigung führt letztlich dazu, dass der Werkstoff in diesen betroffenen Bereichen die Materialbindung vollständig verliert und dadurch eine Materialtrennung auftritt.
Ab diesem Zeitpunkt haben wir einen makroskopischen Riss vorliegen, welchen wir dann wieder im Rahmen der Bruchmechanik mit Prüfungen wie dem Kompakt-Zugversuch näher untersuchen können.
Kennt man nun die Geometrie und Beanspruchung der fehlerhaften Stelle, so ist es möglich ein Zähigkeitsmaß zu ermitteln. Mit Hilfe diese Maßes kann man dann Bedingungen formulieren, bei denen bei einer fortschreitenden Belastung ein unerwünschtes Risswachstum mit anschließenden Bruch die Folge ist. Der Bruch tritt mit der Überschreitung der Bruchfestigkeit ein.
Die Unempfindlichkeit eines Werkstoffes wird mit Hilfe der Bruchzähigkeit ![]() beschrieben!
beschrieben!
Diese Kenngröße wird alternativ als Risszähigkeit oder Risswiderstand bezeichnet und gibt uns Auskunft über den Widerstand des Werkstoffes gegenüber Riss-Initiierung.
Riss und Bruch am Werkstoff – Ursachen
Risse lassen sich leider vielen Bereichen des Maschinenbaus nicht vermeiden. Damit man jedoch nicht wöchentlich die Maschinen zerlegen muss um das betroffene Bauteil auszutauschen, weil sich mal wieder ein Riss gebildet hat, sollte man im Vorfeld die Werkstoffe so auswählen, dass sie unempfindlich auf eine Rissbildung reagieren. Auf Kleinstrisse sollte der Werkstoff im Normalfall gar nicht reagieren. Soll heißen: Keine Rissausbreitung und kein Bruch!
Dennoch nimmt die Bruchmechanik in allen Konzepten an, dass bereits ein Riss (als existierende Fehlstelle) im Bauteil vorhanden ist.
Rissbildung innerhalb der Herstellungsphase
Der Ursprung kann bereits im Herstellungsprozess liegen. Hier treten unter anderem:
- Lunker,
- Einschlüsse,
- Spannungsrisse
auf.
Lunker und Einschlüsse treten innerhalb des Urformens durch Gießen, Extrudieren oder Sintern auf. Spannungsrisse stehen eher in der anschließenden Abkühlphase oder während einer Wärmebehandlung.
Rissbildung innerhalb der Nutzungsdauer
Alternativ entsteht der Riss aber erst innerhalb der Nutzungsdauer des Bauteils. Hier treten Risse unter anderen durch
- Zyklische Beanspruchungen
- Dynamische Beanspruchungen
auf.
Zyklische als auch dynamische Beanspruchungen treten regelmäßig an unterschiedlichsten Bauteilen auf. Vorrangig jedoch an Bauteilen des Maschinenbaus, wie Nockenwellen oder Getriebebestandteilen.
Rissausbreitung – Ursache
Ein Riss entsteht nicht einfach aus dem Nichts. Auch das Wachstum eines Risses hat eine Ursache. Damit beide Vorgänge ablaufen wird Energie benötigt, denn in beiden Fällen vergrößert sich die Werkstoffoberfläche.
Auf der anderen Seite wird aber auch Energie, welche im Werkstoffgefüge als elastische Energie wirkt, frei.
Überwiegt die Freisetzung von elastische Energie, so setzt sich die Rissausbreitung im Werkstoff fort kontinuierlich fort.
Wie stark letztlich die Rissausbreitung ausfällt, hängt im Wesentlichen von zwei Gruppen von Faktoren ab:
Widerstandsfähigkeit des Werkstoffes
Die Widerstandsfähigkeit eines Werkstoffes orientiert sich an internen Faktoren (Werkstoffzustand) und externen Faktoren (Umgebungsparameter).
Zu den internen Faktoren zählen:
- Werkstoffalter (Gefügezustand)
- Werkstoffporösität
- Sprödverhalten des Werkstoffes
- Anteil an Legierungselementen
Zu den externen Faktoren zählen:
- Temperaturen (niedrig, hoch)
- Relative Feuchtigkeit ( feucht, trocken)
Belastung und Geometrie des Werkstoffes
Die Widerstandsfähigkeit eines Werkstoffes orientiert sich hier an drei Faktoren:
- Art der Belastung
- Geometrie der Werkstoffprobe
- Geometrie der Kerbe
Bei der Art der Belastung unterscheidet man zwischen:
- Zugbeanspruchung
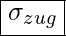
- Druckbeanspruchung
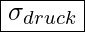
- Biegebeanspruchungen
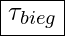
- Torsionsbeanspruchung
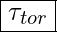
Bei der Geometrie der Werkstoffprobe berücksichtigen wird:
- Probenhöhe
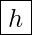
- Probenlänge
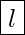
- Probenbreite
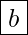
- Probendurchmesser
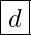 [Zylindrische Proben]
[Zylindrische Proben]
Die Geometrie der Kerbe beinhaltet folgende Größen:
- Rissweite
- Risswinkel
- Risstiefe
Kompakt-Zugversuch (Risszähigkeitsversuch) – Grundlagen
Der Kompakt-Zugversuch (Risszähigkeitsversuch) hilft uns den Widerstand eines Werkstoffes gegen eine instabile Ausbreitung eines Risses zu ermitteln. Die Größe, die uns eine stichhaltige Aussage dazu liefert ist der Spannungsintensitätsfaktor ![]() .
.
“Der Spannungsintensitätsfaktor beschreibt den Punkt, ab welchem ein instabiler Rissfortschritt einsetzt.”
“Genaue Anweisungen für die Durchführung dieses Versuches finden sich in der DIN EN ISO 12737.”
Kompakt-Zugversuch – Probenform
Die Werkstoffprobe für den Risszähigkeitsversuch kann unterschiedliche Geometrien aufweisen.
So kann die Probe
- Stab (balkenartig)
- kubisch (Würfel)
oder
- zylindrisch (rund)
gestaltet werden.
Kompakt-Zugversuch – Prinzip
Als Untersuchungsgegenstand dient eine Werkstoffprobe auch Zugprobe genannt, die eine winkelförmige Kerbe aufweist.
Liegt eine Zugprobe aus einem sehr spröden Werkstoff wie einer Keramik vor, so erfordert das Ankerben besondere Sorgfalt. Hier haben sich zwei Techniken durchgesetzt:
- Single edge V-notched beam (SEVNB): Hier wird die Probe im ersten Schritt angesägt und anschließend eine 4-Punkt-Biegeversuch durchgeführt.
- Indentation strength in bending (ISB): Hier wird die Probe mit Hilfe einer Vickerspyramide (Diamantpyramide) angekerbt.
Zudem weist die Probe in vielen Fällen zwei kreisrunde Bohrungen an den äußeren Enden auf, an denen jeweils eine Last aufgebracht wird. Durch die beiden kontinuierlichen Kräfte, die beide parallel zur Kerbe wirken, wird die Probe auseinandergezogen.
Während der gesamten Versuchsdauer werden sowohl die Rissöffnungsänderung ![]() als auch die Risslänge
als auch die Risslänge ![]() in gleichmäßigen Abständen gemessen. Diese beiden Werte beschreiben die Rissausdehnung.
in gleichmäßigen Abständen gemessen. Diese beiden Werte beschreiben die Rissausdehnung.
Zudem wird die Spannung erfasst, bei welcher der Riss instabil wird.
- Handelt es sich bei der Probe um einen Balken, so erfolgt die Versuchsdurchführung mit zwei Druckkräften, die jeweils auf der gegenüberliegenden Seite eine Rissausbreitung in der Kerbe verursachen.
- Liegt hingegen ein Kubus oder ein Zylinder als Probenform vor, so erfolgt die Rissausbreitung durch zwei entgegengesetzt wirkende Zugkräfte, welche die in der Probenmitte befindliche Kerbe vergrößern.
Rissbeanspruchung – Arten (Übersicht)
Innerhalb der Bruchmechanik unterscheiden wir drei Beanspruchungsarten, auch Modi genannt, um einen Riss zu beanspruchen. Diese können einzeln, aber auch in Kombination zusammen auftreten.
Modus 1 (Öffnen der Rissflanken)
Hier werden alle Belastungen aufgeführt, die normal zur Rissfront wirken.
Der Riss wirkt dabei senkrecht zur Normalspannung und lässt sich bei Bauteilen beobachten, die unter Zug- oder Biegebelastungen stehen.
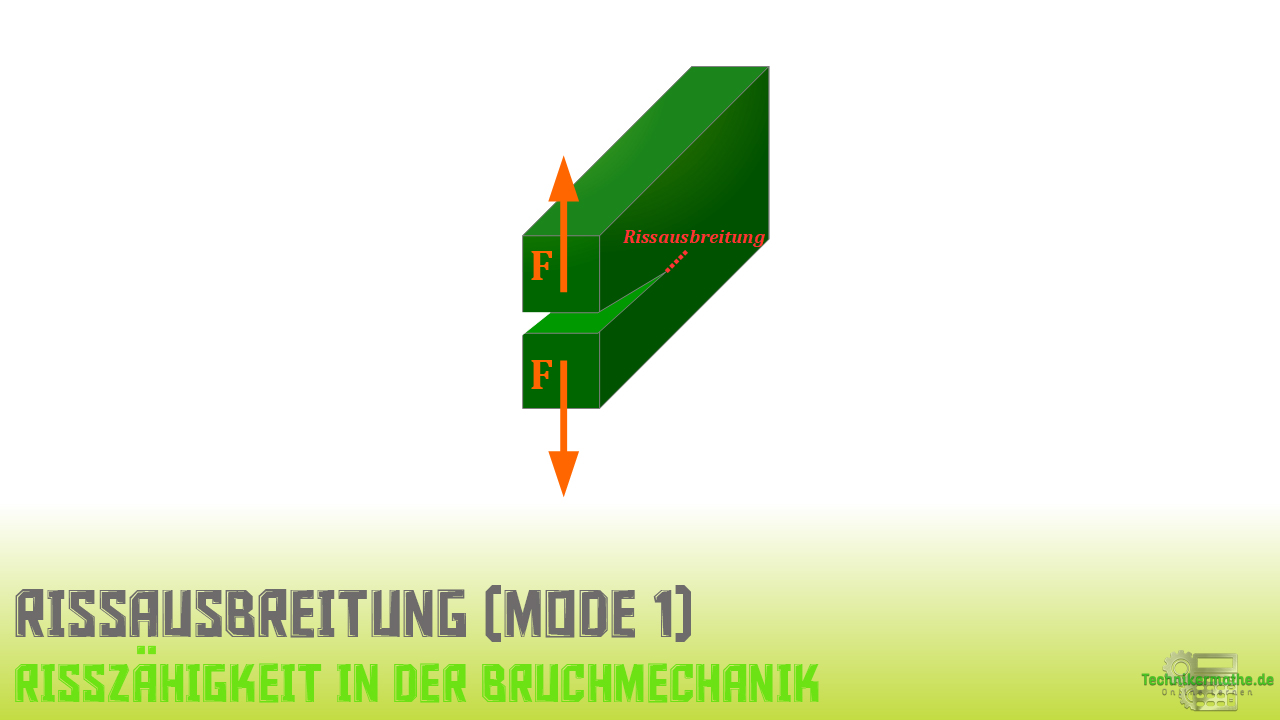
Modus 2 (Entgegengesetzte Verschiebung der Rissflanken in Rissausbreitungsrichtung)
Hier werden alle Belastungen erfasst, die eine entgegengesetzte Verschiebung der Rissflanken in Rissausbreitungsrichtung hervorrufen.
Dieser Vorgang erfolgt in den meisten Fällen durch eine Schubbelastung.
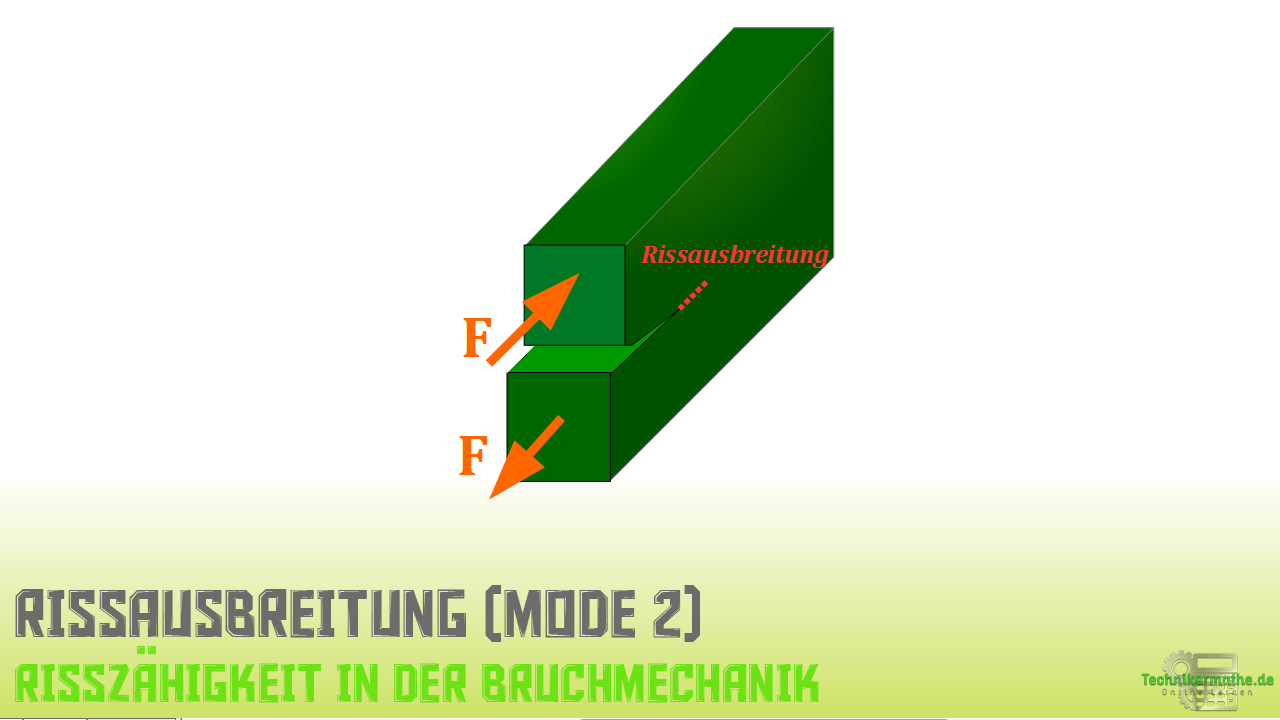
Modus 3 (Verschiebung der Rissflanken in Rissausbreitungsrichtung)
Hier werden alles Belastungen erfasst, die eine Verschiebung der Rissflanken quer zur Rissausbreitungsrichtung bewirken.
Dabei wird der Werkstoff gestaucht. Bei einer Welle bewirkt eine Torsionsbeanspruchung einen Riss senkrecht zur Wellenachse.
Sonderfall: Mixed-Mode
Eine Mixed-Mode-Beanspruchung stellt einen Sonderfall dar, denn hier treten alle drei Modi gemeinsam an der Rissfront auf.
Verursacht wird diese Beanspruchung durch mehrachsige von außen wirkende Belastungen am Bauteil.
Es muss jedoch auch erwähnt werden, dass einachsige Belastungen diese Beanspruchung hervorrufen können, sofern sie unter einem nicht orthogonalen Winkel zur Achse der Hauptnormalspannung wirkt.
Kompakt-Zugversuch (Risszähigkeitsversuch) – Aufbau
Nachfolgend siehst du die schematische Darstellung des Kompakt-Zugversuch.
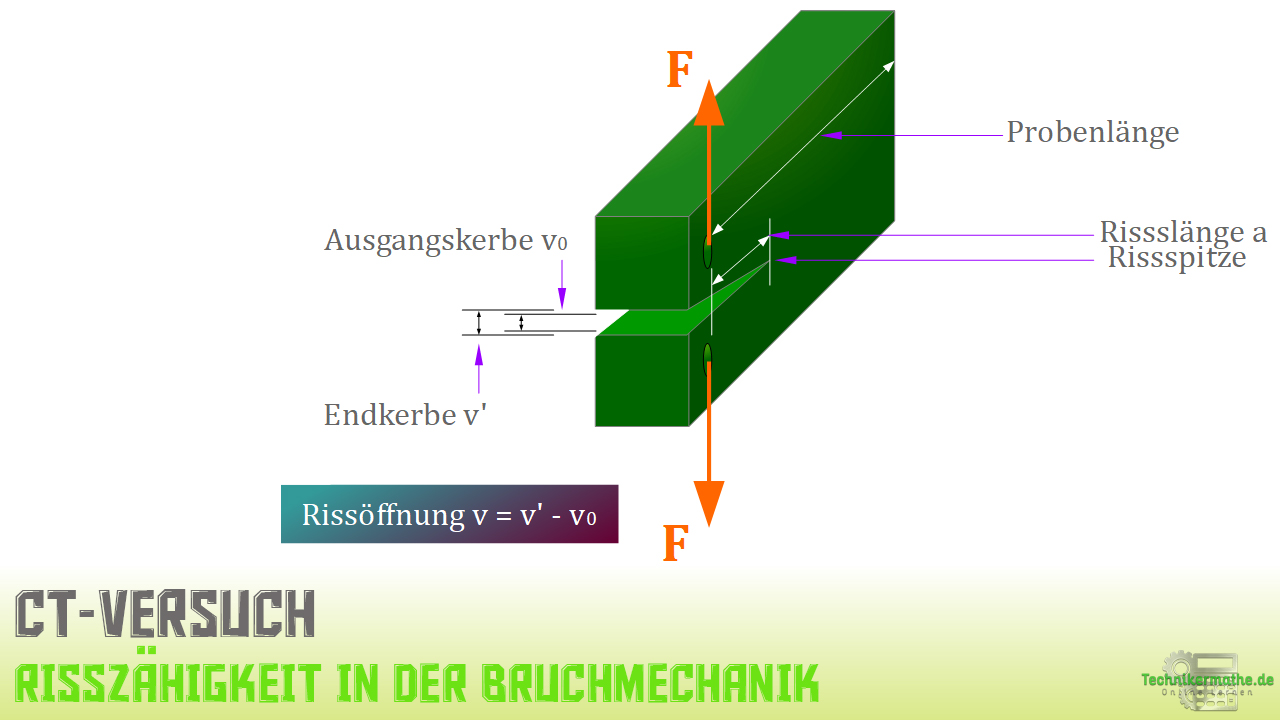
Kompakt-Zugversuch (Risszähigkeitsversuch) – Prüfergebnisse
Nachfolgend siehst du die Darstellung der Prüfergebnisse aus dem Kompakt-Zugversuch in einem Rissöffnungsdiagramm.
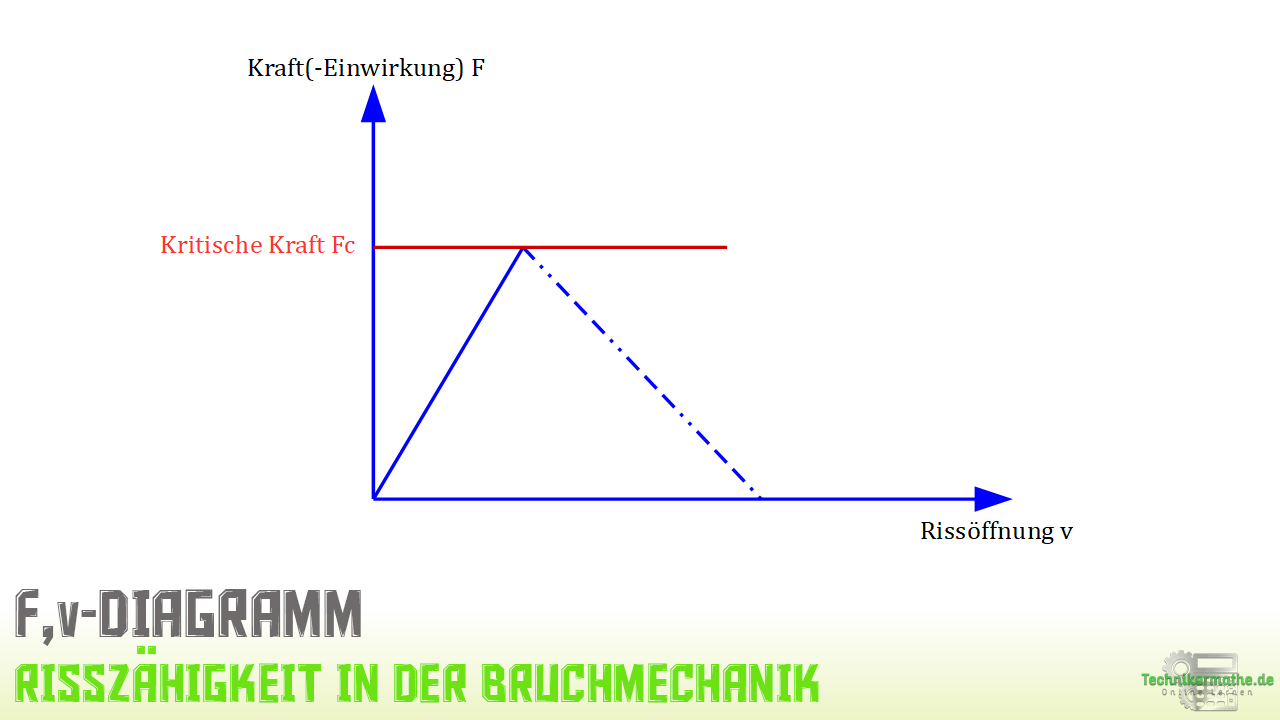
Kompakt-Zugversuch (Risszähigkeitsversuch) – Berechnungen
Wie bereits oben erwähnt interessiert den Werkstoffprüfer besonders der Spannungsintensitätsfaktor. Noch interessanter ist der kritische Spannungsintensitätsfaktor ![]() , also der Punkt, in welchem die Rissausbreitung einsetzt.
, also der Punkt, in welchem die Rissausbreitung einsetzt.
“Soll der Riss sich nicht weiter ausbreiten so muss die Intensität der Spannung unterhalb dieses Wertes verbleiben.”
Spannungsintensitätsfaktor
Der Spannungsintensitätsfaktor ermittelt sich über folgende Gleichung:
![]()
Kennzahlen:
![]() Spannungsintensitätsfaktor
Spannungsintensitätsfaktor
![]() Spannung, anliegt und im Bereich um die Kerbe herum wirkt.
Spannung, anliegt und im Bereich um die Kerbe herum wirkt.
![]() Rissgrößenparameter (Risslänge/Risstiefe)
Rissgrößenparameter (Risslänge/Risstiefe)
![]() Korrekturfaktor (Geometriefaktor)
Korrekturfaktor (Geometriefaktor)
Korrekturfaktor
Der Korrekturfaktor berücksichtigt zwei Tatsachen:
- Sind die Proben nicht unendlich groß, so besteht immer eine Abhängigkeit des Spannungsintensitätsfaktors den den Abmessungen der Proben.
- Es stellt sich ein ebener Spannungszustand ein, da an den Rissenden senkrecht zur Oberfläche keine Spannungen auftreten.
Berechnet wird dieser wie folgt:
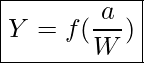
Mit zunehmender Probendicke spielt der Geometriefaktor nur noch eine untergeordnete Rolle und kann dann in der Berechnung weggelassen werden:
![]()
Kritischer Spannungsintensitätsfaktor
Der kritische Spannungsintensitätsfaktor ![]() oder
oder ![]() ermittelt sich über folgende Gleichung:
ermittelt sich über folgende Gleichung:
![]()
Kennzahlen:
![]() Spannungsintensitätsfaktor
Spannungsintensitätsfaktor
![]() Spannung, anliegt und im Bereich um die Kerbe herum wirkt.
Spannung, anliegt und im Bereich um die Kerbe herum wirkt.
![]() kritische Rissgrößenparameter (kritische Risslänge/Risstiefe)
kritische Rissgrößenparameter (kritische Risslänge/Risstiefe)
![]() Korrekturfaktor (Geometriefaktor)
Korrekturfaktor (Geometriefaktor)
Einheit des Spannungsintensitätsfaktor
Die Einheit in der das Messergebnis angegeben wird ist:
![]()
bzw.
![]()
Liegen zwei gleiche Werkstoffe vor, so sinkt die Risszähigkeit mit steigender 0,2 % Streckgrenze.
Bei steigender Temperatur nimmt die Risszähigkeit des Werkstoffes zu.
Kompakt-Zugversuch – Risszähigkeit ausgewählter Werkstoffe
Die Risszähigkeit zwischen den unterschiedlichen Werkstoffe variiert sehr stark. Das zeigt sich auch in der Versuchsergebnissen beim Kompakt-Zugversuch.
Keramiken
Keramiken und die meisten Polymere (Kunststoffe) besitzen einer sehr niedrige Risszähigkeit. Diese Liegt in einem Bereich von ![]() bis
bis ![]() . Der Spannungsintensitätsfaktor ist hier niedrig.
. Der Spannungsintensitätsfaktor ist hier niedrig.
Werte des kritischen Spannungsintensitätsfaktor aus dem Kompakt-Zugversuch für ausgewählte Keramiken und Polymere:
![]() – Beton
– Beton
![]() – Siliciumkarbid
– Siliciumkarbid
![]() – Aluminiumoxid
– Aluminiumoxid
![]() – Polymethylmathacrylat
– Polymethylmathacrylat
![]() – Polystyrol (PS, Thermoplaste)
– Polystyrol (PS, Thermoplaste)
Verbundstoffe
Verbundstoffe haben eine mittlere Risszähigkeit. Stahlbeton besitzt eingelagerte Teilchen und Fasern, wodurch sich die Risszähigkeit erhöhen lässt. Denn die Fasern wirken duktil und sorgen dafür, dass für eine Rissausbreitung zusätzliche Energie benötigt wird. Der Spannungsintensitätsfaktor liegt hier im Mittelfeld.
Werte des kritischen Spannungsintensitätsfaktor aus dem Kompakt-Zugversuch für ausgewählte Verbundstoffe:
Metalle
Metalle und Metalllegierungen besitzen aufgrund ihrer Kristallstruktur eine sehr hohe Risszähigkeit. Diese liegt bis zu 100-fach höher als bei Keramiken. Der Spannungsintensitätsfaktor ist hier sehr hoch.
Werte des kritischen Spannungsintensitätsfaktor aus dem Kompakt-Zugversuch für ausgewählte Metalle und Metalllegierungen:
![]() – Stahl
– Stahl
![]() – Aluminium
– Aluminium
![]() – Aluminiumlegierung
– Aluminiumlegierung
![]() – Titanlegierung
– Titanlegierung
“Nach dem Kompakt-Zugversuch mit Bestimmung der Kerbschlagarbeit erklären wir dir im kommenden Kurstext die indirekte Härteprüfung inklusive der wichtigen Verfahren.”
Was gibt es noch bei uns?
Tausende interaktive Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Das erwartet dich!
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Auszüge aus unserem Kursangebot!
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++
Oder direkt >> Mitglied << werden und >> Zugriff auf alle 26 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 7,40 EUR/Monat
++ Besser geht’s nicht!! ++
Technikermathe.de meets Social-Media
Dein Technikermathe.de-Team






