[ME1] Biegebeanspruchung – Biegung im Maschinenbau [Grundlagen, Berechnungen, Beispiele]

In diesem Kurstext gehen wir auf die Beanspruchungsart Biegung in der Maschinentechnik näher ein. Dabei behandeln wir alles rund um das Thema Biegebeanspruchung.

Für ein optimales Verständnis helfen dir einige anschauliche Beispiele und abschließende, umfangreiche Abbildungen zu dem Thema, sowie ein zusammenfassender Videoclip.

Biegebeanspruchung – Definition

Die Biegung bzw. Biegebeanspruchung ist ein physikalischer Vorgang, bei welchem ein Körper oder ein Material unter einer Last oder Belastung in eine gekrümmte Form gebracht wird.

Merk’s dir!

In der Mechanik bezieht sich Biegung auf die Verformung eines Objekts entlang seiner Längsachse, wobei eine Kraft auf das Material in einem Winkel zur Längsachse aufgebracht wird. Diese Kraft erzeugt ein Drehmoment, das zu einer Krümmung des Objekts führt.

Biegebeanspruchung - Biegung im Alltag und Maschinenbau — Biegebeanspruchung – Biegung im Alltag und Maschinenbau

Biegung tritt häufig bei Materialien wie Metallen, Kunststoffen oder Holz auf, wenn sie unter Druck, Zug oder Biegemomenten beansprucht werden. Zum Beispiel können Stahlträger in Brücken oder Gebäuden unter Lasten gebogen werden, um Kräfte zu verteilen und Belastungen aufzunehmen.

Fassen wir zusammen, dass die Biegung selbst durch den Einfluss von

Querkräften
Biegemoment
Kräftepaaren

in geometrischen Körpern des Maschinenbaus wie

Wellen
Balken
Trägern

oder

Achsen

auftritt.

Biegebeanspruchung – Formen

Wir können 4 unterschiedliche Formen der Biegebeanspruchung unterscheiden und in zwei Kategorien einteilen:

Reine Biegung [Art der Biegung]
Querkraftbiegung [Art der Biegung]
Gerade Biegung [Wirkrichtung der Biegung]
Schiefe Biegung [Wirkrichtung der Biegung]

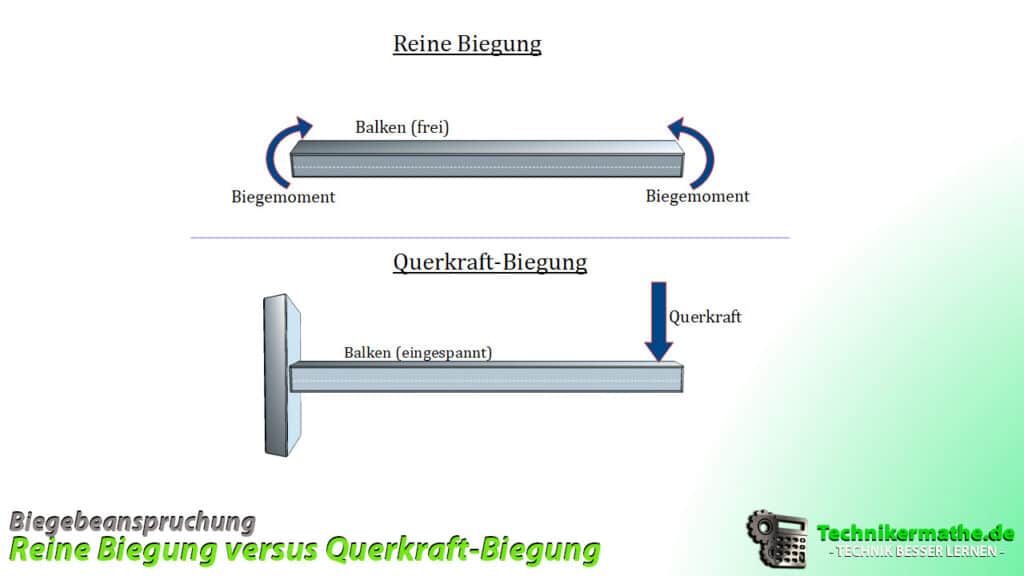
Reine Biegung – Erklärung

Die reine Biegung ist eine querkraftfreie Biegung, bei welcher die Verformung durch das Aufbringen zweier Biegemoment an den jeweiligen Enden eines Bauteil [häufig Balken] auftritt. Da es keine vertikal gerichteten Kräfte (Querkräfte) gibt, treten hier nur Normalspannungen $\sigma$ auf.

Lange Ausführung!

Eine reine Biegung ist eine Biegebelastung, bei der die Kräfte senkrecht zur Biegeachse verlaufen und es keine Torsionsbelastung gibt. Das bedeutet, dass der Balken oder das Bauteil nur in einer Ebene gebogen wird, ohne dabei verdreht zu werden.

In einer reinen Biegung entstehen in dem Bauteil Spannungen, die eine Dehnung auf der Zugseite und eine Stauchung auf der Druckseite verursachen. Die maximale Spannung tritt in der neutralen Faser des Bauteils auf, also in dem Bereich, der nicht gedehnt oder gestaucht wird.

Die Theorie der reinen Biegung ist ein wichtiger Bestandteil der Festigkeitslehre und wird bei der Berechnung von Bauteilen wie Balken und Trägern angewendet, um deren Belastbarkeit zu bestimmen. Eine reine Biegung tritt in der Praxis jedoch selten auf, da die meisten Bauteile auch einer gewissen Torsionsbelastung ausgesetzt sind.

Querkraft-Biegung – Erklärung

Anders als bei der reinen Biegung wirken bei der Querkraft-Biegung vertikale Kräfte (Querkräfte) auf das Bauteil und erzeugen eine Verformung. Zusätzlich zum Biegemoment, welches die Normalspannungen $\sigma$ erzeugt, bewirken die Querkräfte ein Auftreten von Schubspannungen $\tau$ innerhalb des Bauteils.

Lange Ausführung!

Die Querkraftbiegung ist eine Art der Biegebelastung, bei der zusätzlich zur reinen Biegung eine Querkraft auf das Bauteil wirkt. Die Querkraft ist dabei eine Kraft, die senkrecht zur Längsachse des Bauteils verläuft.

Bei der Querkraftbiegung entsteht in dem Bauteil eine Schubspannung senkrecht zur Biegeachse. Diese Schubspannung verursacht eine Scherung im Bauteil, die sich in Form von Scherkräften und Scherbeanspruchungen manifestiert.

Die Querkraftbiegung tritt in vielen Bauteilen auf, insbesondere in Trägern und Balken. Eine unzureichende Berücksichtigung der Querkraftbelastung kann zu einer Schwächung des Bauteils führen und im schlimmsten Fall zu dessen Versagen führen.

Die Berechnung der Querkraftbiegung ist daher ein wichtiger Bestandteil der Festigkeitslehre und wird bei der Auslegung und Konstruktion von Bauteilen berücksichtigt. Dabei werden sowohl die Kräfte in der Längs- als auch in der Querrichtung berücksichtigt, um eine sichere und zuverlässige Konstruktion zu gewährleisten.

Gerade Biegung – Erklärung

Die gerade Biegung kennzeichnet, dass die Biegung eines Bauteils in die Richtung einer der Hauptachsen des Bauteilquerschnitts stattfindet. Wir nehmen an, dass es sich bei dem Bauteil um ein symmetrisches Objekt handelt.

Lange Ausführung!

Eine gerade Biegung ist eine Art von Biegebelastung, bei der ein Bauteil entlang einer geraden Linie gebogen wird. Dies bedeutet, dass das Bauteil in einer Ebene gebogen wird, ohne dabei verdreht zu werden.

Bei einer geraden Biegung entstehen im Bauteil Spannungen, die eine Dehnung auf der Zugseite und eine Stauchung auf der Druckseite verursachen. Die maximale Spannung tritt in der neutralen Faser des Bauteils auf, also in dem Bereich, der nicht gedehnt oder gestaucht wird.

Eine gerade Biegung kann in vielen verschiedenen Bauteilen auftreten, zum Beispiel in Trägern, Balken oder Stangen. Sie kann durch äußere Kräfte oder Lasten verursacht werden, die auf das Bauteil einwirken.

Die Berechnung der Spannungen und Verformungen in einem Bauteil unter gerader Biegung ist ein wichtiger Bestandteil der Festigkeitslehre und wird bei der Konstruktion von Bauteilen berücksichtigt, um deren Belastbarkeit zu bestimmen. Eine zu starke Biegung kann zu einem Versagen des Bauteils führen, weshalb die Auslegung von Bauteilen unter Biegebelastung sorgfältig durchgeführt werden muss.

Unterscheidung Reine Biegung und Querkraftbiegung!

Schiefe Biegung – Erklärung

Die schiege Biegung zeichnet aus, dass die Biegung des Bauteils in eine von den Hauptachsen abweichenden Richtung stattfindet. Sie tritt ebenfalls auf, wenn ein Bauteil keinen symmetrischen Querschnitt [Profil] besitzt. Letzteres verursacht dann ein weiteres Biegemoment in Wirkrichtung eine anderen Achse.

Lange Ausführung!

Eine schiefe Biegung ist eine Art von Biegebelastung, bei der ein Bauteil entlang einer schiefen Linie gebogen wird, d.h. eine Biegung, die nicht in einer Ebene verläuft. Dabei wirken Kräfte, die nicht senkrecht zur Biegeachse verlaufen, auf das Bauteil ein.

Im Gegensatz zur geraden Biegung, bei der das Bauteil nur in einer Ebene gebogen wird, führt die schiefe Biegung zu einer Kombination aus Biege- und Torsionsbelastungen, die eine komplexe Spannungsverteilung im Bauteil verursachen können.

Die Berechnung von Bauteilen unter schiefen Biegebelastungen ist daher aufwändiger und erfordert in der Regel numerische Methoden, wie z.B. die Finite-Elemente-Methode (FEM), um die Belastung und Spannungen im Bauteil genau zu berechnen. Dabei müssen sowohl die Biege- als auch die Torsionsbeanspruchungen berücksichtigt werden, um eine sichere Konstruktion zu gewährleisten.

Eine schiefe Biegung kann in vielen verschiedenen Bauteilen auftreten, wie z.B. in Wellen, Rohren oder Flugzeugflügeln. Die Auswirkungen einer schiefen Biegung auf die Belastbarkeit des Bauteils können je nach Art des Bauteils und der Belastung unterschiedlich sein und erfordern eine sorgfältige Analyse und Berechnung.

Biegespannung – Formel

Wir können innerhalb einer Biegebeanspruchung die Biegespannung mit einer Formel beschreiben, welche ein Verhältnis zwischen dem Biegemoment M und dem Trägheitsmoment I eines Querschnitts beinhaltet.

Biegespannung

$\sigma = \frac{M \cdot y}{I}$

Kennzahlen:

$\sigma =$ Biegespannung [Belastung des Materials im Querschnitt]

$M =$ Biegemoment

$y =$ Abstand des Querschnitts von der neutralen Faser

$I =$ Trägheitsmoment des Querschnitts [Widerstandsfähigkeit gegen Biegung]

Auch interessant…

Die Biegespannung σ variiert entlang des Querschnitts und erreicht bei der weitesten Entfernung von der neutralen Faser ihr Maximum. Daher ist es wichtig, sich ein Material mit ausreichendem Trägheitsmoment auszusuchen, um eine zu hohe Biegespannung zu vermeiden, die mit einem Bruch des Materials zum Bauteilversagen führen kann.

Bestimmung der Biegebeanspruchung – Vorgehensweise

Um ein Biegemoment zu ermitteln, schneidet man gedanklich durch das Bauteil [hier Balken] und trägt anschließend alle Schnittgrößen ein. Zu den Schnittgrößen zählen

Querkraft
Normalkraft
Biegemoment

Schnitte am ebene Balken führt man immer dann durch, wenn unstetige Belastungen [Belastungswechsel] vorliegen.

Folglich können wir dann den Verlauf der Biegemomente für die einzelnen Abschnitte bestimmen.

Für dein besseres Verständnis betrachten wir einen Balken, welcher einer Querkraft-Biegung ausgesetzt wird und ein symmetrisches Profil besitzt.

Biegung - Beispiel: Wellenlager abstützen — Biegung – Beispiel: Wellenlager abstützen

Vorgehensweise

Bestimmung der Funktion
Einzeichnen der wirkenden Kräfte
Erzeugen eines mechanischen Ersatzbildes
Bestimmung der Auflagerkräfte [Schnittmethode]
Bestimmung der Schnittgrößen [Schnittmethode]
Einzeichnen der Schnittgrößenverläufe

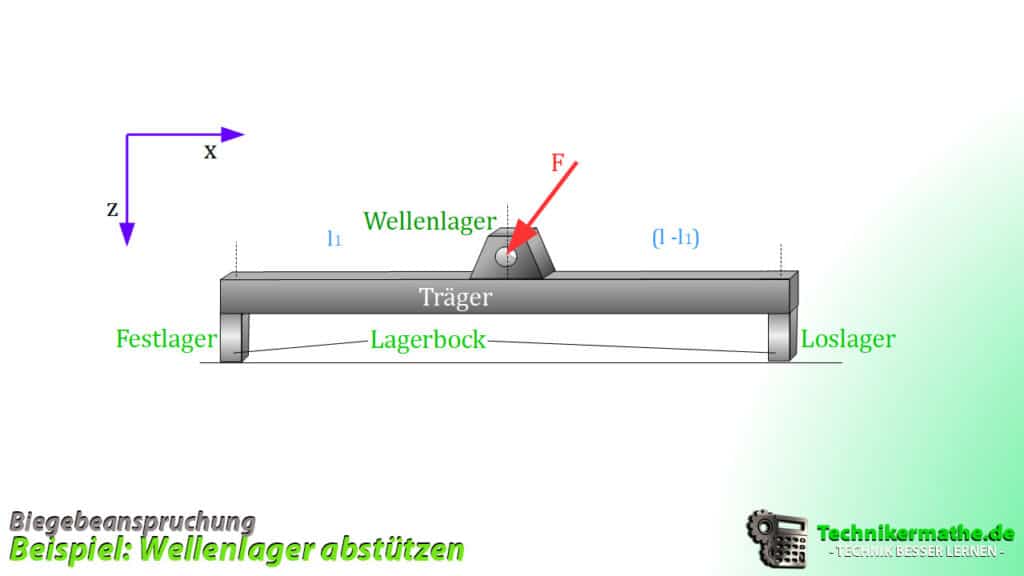
Bestimmung der Funktion

Eine Welle wird in einem Lager abgestützt, wobei sich das Lager auf einem Träger befindet, welcher selbst auf einem Lagerbock aufliegt.

Einzeichnen der wirkenden Kräfte

Nun zeichnen wir alle für unsere Berechnungen notwendigen Kräfte ein. In unserem Fall wirkt die Kraft $F$ schräg auf das Lager.

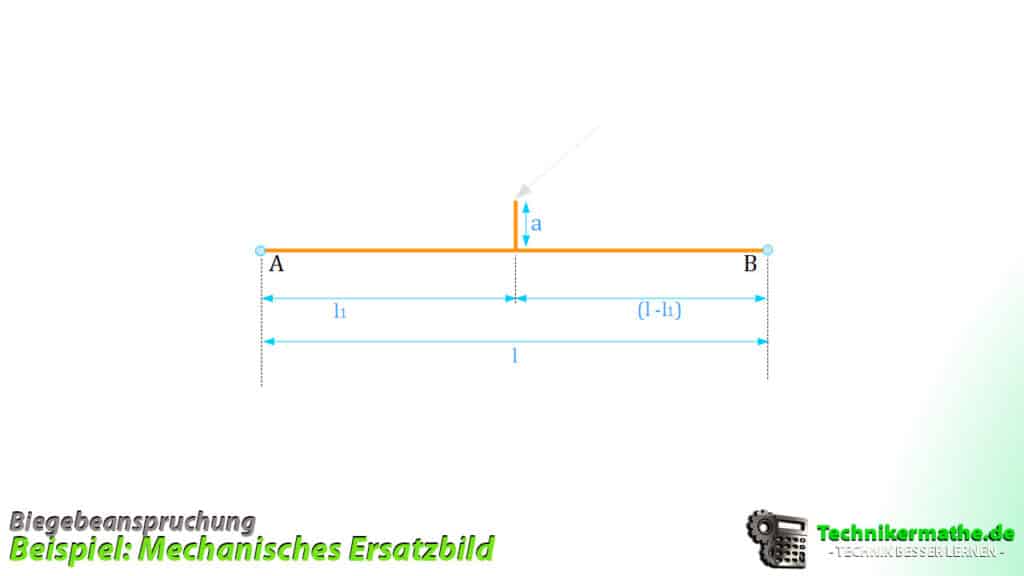
Erzeugen eines mechanischen Ersatzbildes

Ausgehend von unserer Realdarstellung erzeugen wir ein mechanisches Ersatzbild, welches alle Bereiche auf ein Minimum reduziert. Im weiteren Verlauf [4. und 5.] vervollständigen wir das Ersatzbild mit den ermittelten Größen.

Bestimmung der Auflagerkräfte

Für die weiteren Berechnungen nehmen wir die z-Achse nach unten gerichtet und die x-Achse nach nach rechts gerichtet an. Alle Schnittgrößen in positive Achsenrichtung werden positiv berücksichtigt, alle Schnittgrößen, die in negative Achsenrichtung zeigen, dementsprechend negativ. Linksdrehende Momente sind positive Momente, rechtsdrehende Momente negative Momente.

Zu Beginn schauen wir uns die Lager A und B an und ermitteln die dort wirkenden Biegemomente. Hierzu stellen wir für jedes Lager die Momentengleichung auf.

Lager A – Momentengleichung

$\curvearrowleft A: B_z \cdot l - F_z \cdot l_1 + F_x \cdot a = 0$

Auflösen der Gleichung nach $B_z$ ergibt:

$B_z = \frac{ F_z \cdot l_1 + F_x \cdot a}{l}$

Lager B – Momentengleichung

$\curvearrowleft B: - A_z \cdot l + F_z \cdot (l - l_1) + F_x \cdot a = 0$

Auflösen der Gleichung nach $A_z$ ergibt:

$A_z = \frac{ F_z \cdot (l - l_1) + F_x \cdot a}{l}$

Im nächsten Schritt stellen wir die horizontale und vertikale Gleichgewichtsbedingung für beide Lager auf.

Lager A – Horizontale Gleichgewichtsbedingung

$\rightarrow : A_x - F_x = 0$

Ergibt

$A_x = F_x$

Lager A – Vertikale Gleichgewichtsbedingung

$\downarrow : -A_z - B_z + F_z = 0$

Ergibt

$A_z = - B_z + F_z$

Lager A – Vertikale Gleichgewichtsbedingung

$\downarrow : -A_z - B_z + F_z = 0$

Ergibt

$B_z = - A_z + F_z$

Diese ermittelten Größen übertragen wir jetzt wieder in unser mechanisches Ersatzbild:

Biegebeanspruchung - Mechanisches Ersatzbild — Biegebeanspruchung – Mechanisches Ersatzbild

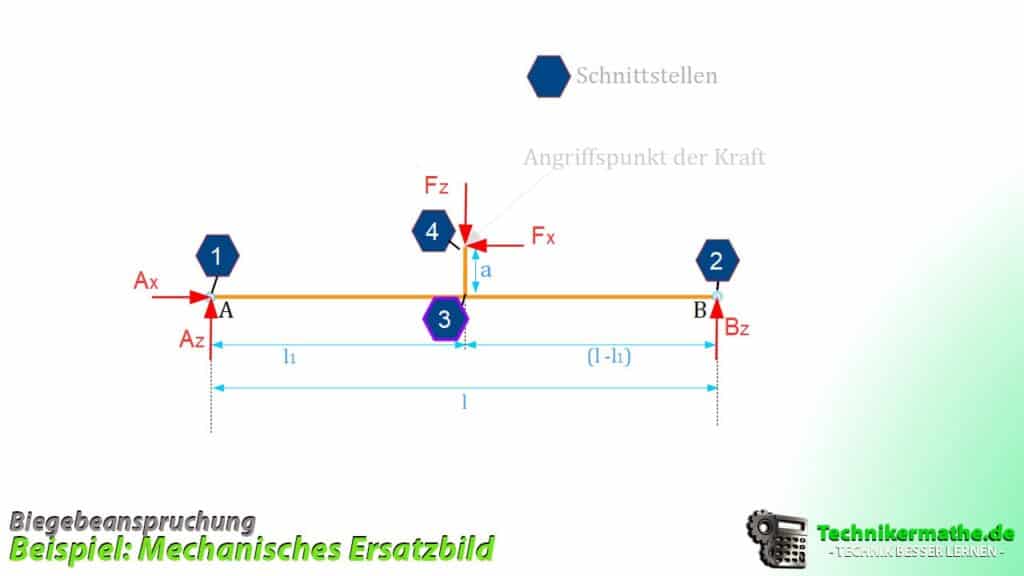
Bestimmung der Schnittgrößen

Wir bestimmen die Schnittgrößen unter Hinzunahme des Ersatzbildes. Wir können 4 Bereiche für Schnittstellen festmachen, die farblich markiert sind.

Dabei zeigt sich, dass in dem Bereich der Schnittstelle 3 ebenfalls drei Schnittstellen festgelegt werden können – $3_{links}, 3_{rechts}, 3_{oben}$ . Somit liegen insgesamt 6 Schnittstellen vor.

Wir betrachten jetzt jede diese Schnittstellen einzeln und bestimmen folgende Größen:

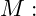$M :$ Biegemoment
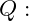$Q :$ Querkraft
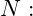$N :$ Normalkraft

Wiederholung: Was sind Schnittufer…

Bei einem Schnitt durch ein Bauteil entstehen zwei Schnittufer, welche auch das Schnittflächen bezeichnet werden:

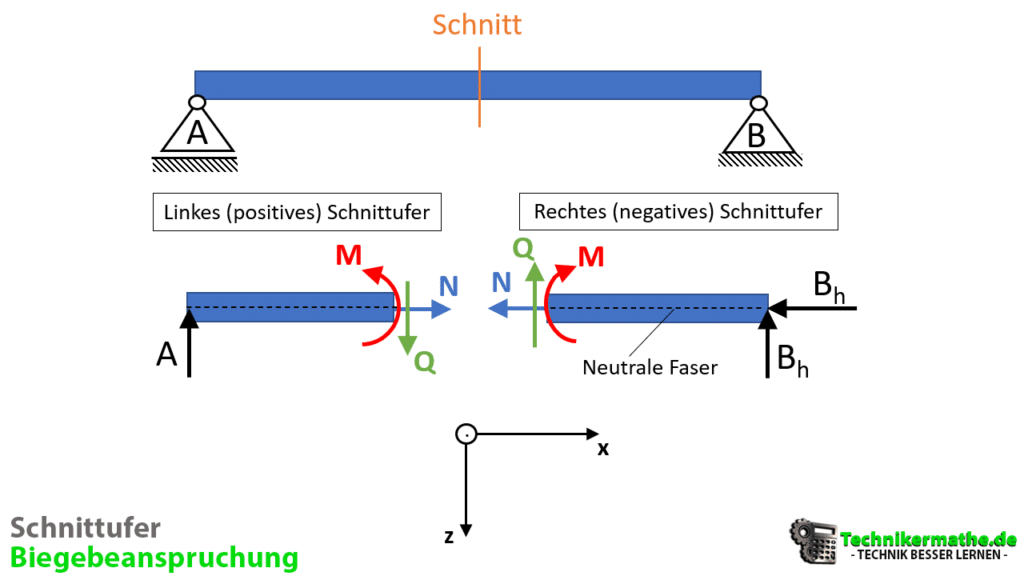
Biegebeanspruchung, Schnittufer, Schnittgrößen, Normalkraft, Querkraft, Biegemoment, Schnittufer

Links haben wir das positive Schnittufer und rechts haben wir das negative Schnittufer festgelegt. Diese Schnittufer werden so bezeichnet, weil wir von dem (unten in der Grafik) angegebenen Koordinatensystem ausgehen, bei welchem die x-Achse nach rechts zeigt und die z-Achse nach unten. Die y-Achse musst du dir aus der Grafik herauskommend vorstellen.

Die Schnittgrößen zeigen am positiven Schnittufer in positive Achsenrichtung.

In unserer Darstellung zeigt am positiven Schnittufer (links in Skizze) die Querkraft $Q$ nach unten in Richtung der positiven z-Achse, das Biegemoment $M$ rotiert nach links um die y-Achse und die Normalkraft $N$ zeigt in Richtung der positiven x-Achse.

Anders verhält es sich mit dem negativen Schnittufer (rechts in Skizze). Hier zeigt die Querkraft $Q$ nach oben in Richtung der negative z-Achse, das Biegemoment $M$ rotiert nach rechts um die y-Achse und die Normalkraft $N$ zeigt in die negative Richtung der x-Achse.

Wichtig ist, dass du dir die Richtung der Schnittgrößen an den beiden Schnittufer merkst. Diese berechnest du aus den Gleichgewichtsbedingungen. Die Normalkraft $N$ wird aus der horizontalen Gleichgewichtsbedingung berechnet, die Querkraft $Q$ aus der vertikalen Gleichgewichtsbedingung und das Biegemoment $M$ aus der Momentengleichgewichtsbedingung.

Die Einführung inklusive einer Vielzahl an Beispielen zu den Berechnungen von Schnittgrößen findest du in unserem Onlinekurs TM1-Statik.

Wir starten jetzt mit der Berechnung der Schnittgrößen für das obige Beispiel. Mit Hilfe der jeweiligen Gleichgewichtsbedingungen können wir für jede Stelle die Schnittgrößen ermitteln. Dabei nehmen wir die z-Achse nach unten gerichtet und die x-Achse nach nach rechts gerichtet an. Alle Schnittgrößen in positive Achsenrichtung werden positiv berücksichtigt, alle Schnittgrößen, die in negative Achsenrichtung zeigen, dementsprechend negativ. Linksdrehende Momente sind positive Momente, rechtsdrehende Momente negative Momente.

Es ergeben sich die folgenden Schnittgrößen:

Schnittstelle 1

Wir betrachten den Rand [Linkes Schnittufer]:

$\curvearrowleft: + M = 0$

daraus folgt: $M = 0$

$\downarrow: Q - A_z = 0$

daraus folgt: $Q = A_z$

$\rightarrow: N + A_x = 0$

daraus folgt: $N = - A_x$

Schnittstelle 2

Wir betrachten den Rand [Rechtes Schnittufer]:

$\curvearrowleft: -M = 0$

daraus folgt: $M = 0$

$\downarrow: -Q - B_z = 0$

daraus folgt: $Q = -B_z$

$\rightarrow: - N = 0$

daraus folgt: $N = 0$

Schnittstelle 3links

Wir betrachten das linke Schnittufer:

$\curvearrowleft: M - A_z \cdot l_1 = 0$

daraus folgt: $M = A_z \cdot l_1$

$\downarrow: Q - A_z = 0$

daraus folgt: $Q = A_z$

$\rightarrow: N + A_x = 0$

daraus folgt: $N = - A_x$

Schnittstelle 3rechts

Wir betrachten das rechte Schnittufer:

$\curvearrowleft: - M + B \cdot (l - l_1) = 0$

daraus folgt: $M = B \cdot (l - l_1)$

$\downarrow: -Q - B_z = 0$

daraus folgt: $Q = - B_z$

$\rightarrow: - N = 0$

daraus folgt: $N = 0$

Schnittstelle 3oben

Wir betrachten das rechte Schnittufer:

$\curvearrowleft: - M + F_x \cdot a = 0$

daraus folgt: $M = F_x \cdot a$

$\downarrow: -Q - F_x = 0$

daraus folgt: $Q = - F_x$

$\rightarrow: - N - F_z = 0$

daraus folgt: $N = -F_z$

Schnittstelle 4

Wir betrachten den Rand [Rechtes Schnittufer]

$\curvearrowleft: - M = 0$

daraus folgt: $M = 0$

$\downarrow: -Q - F_x = 0$

daraus folgt: $Q = -F_x$

$\rightarrow: -N - F_z = 0$

daraus folgt: $N = -F_z$

Einzeichnen der Schnittgrößenverläufe

Im letzten Schritt zeichnen wir die Schnittgrößenverläufe nochmals ein.

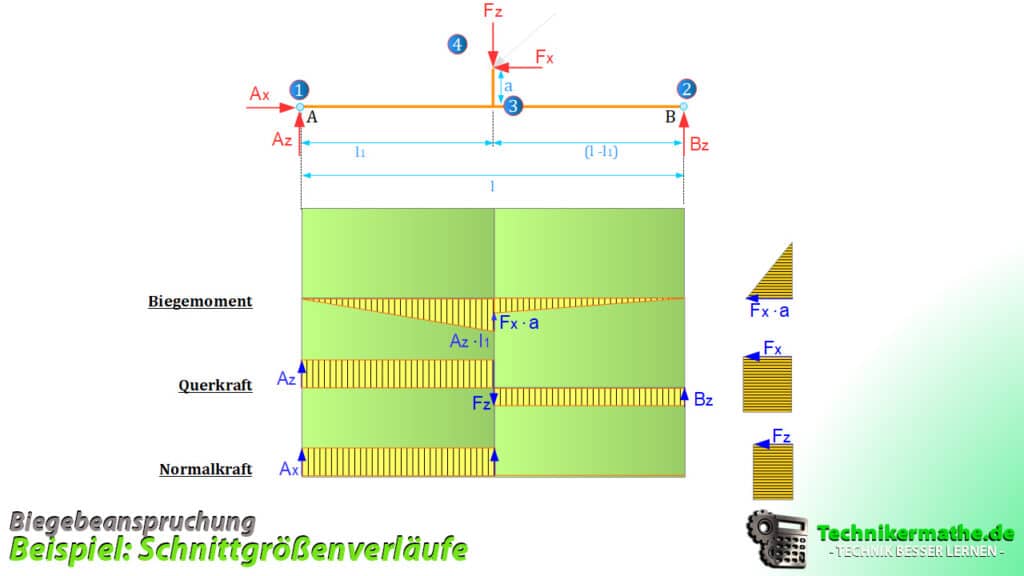
Schnittgrößenverläufe: Biegemoment, Querkraft, Normalkraft

Biegebeanspruchung – Alltagsbeispiele

Die Biegebeanspruchung tritt auf, wenn ein Material durch eine Kombination von Zug- und Druckkräften gebogen wird. Hier sind einige Beispiele für Biegebeanspruchung:

Biegen eines Metallstabes: Wenn ein Metallstab an beiden Enden fixiert ist und eine Kraft in der Mitte aufgebracht wird, entsteht eine Biegebeanspruchung. Der obere Teil des Stabes wird gestaucht (Druckkraft), während der untere Teil gedehnt wird (Zugkraft).
Holzbalken: In einer Holzkonstruktion wie einem Dachstuhl werden Holzbalken verwendet, um das Gewicht des Daches zu tragen. Die Balken werden durch das Gewicht des Daches gebeugt und sind einer Biegebeanspruchung ausgesetzt.
Brückenkonstruktionen: Brücken müssen in der Lage sein, das Gewicht des Verkehrs und anderer Lasten zu tragen. Die Trägerstrukturen der Brücke werden durch die auf sie wirkenden Lasten gebeugt, was zu Biegebeanspruchungen führt.
Regale: Regale oder Bücherregale aus Holz oder Metall werden oft zur Aufbewahrung schwerer Gegenstände verwendet. Wenn die Regalbretter nicht ausreichend stabil sind, können sie sich durch das Gewicht der darauf gelagerten Gegenstände biegen.
Hebel: Ein Hebel ist ein Beispiel für eine mechanische Vorrichtung, die durch Biegebeanspruchung funktioniert. Wenn eine Kraft auf den Hebelarm ausgeübt wird, biegt sich der Hebel und erzeugt eine Hebelwirkung.

Merk’s dir!

Diese Beispiele veranschaulichen, wie die Biegebeanspruchung in verschiedenen Materialien und Strukturen auftritt. Es ist wichtig, die Biegefestigkeit von Materialien zu berücksichtigen, um sicherzustellen, dass sie den auftretenden Biegebelastungen standhalten können.

Was kommt als Nächstes?

Nachdem wir uns mit dem Thema Biegung befasst haben, führen im nächsten Kurstext eine vollständige Berechnung mit Zahlenwerten für das obige Beispiel durch. Im nächsten Kapitel gehen wir dann auf die Torsion als Form der Beanspruchung ein.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++