(WT3-21) -Hookesches Gesetz

“Robert Hooke hat mit dem Hookeschen Gesetz als erster eine Grundlage zur Berechnung von Spannungen und Dehnung sowie deren Proportionalität im linear elastischen Bereich geschaffen.”

Hookesches Gesetz - Lineare elastische Dehnung — Hookesches Gesetz – Lineare elastische Dehnung

Hookesches Gesetz – Grundlagen

Das Hookesche Gesetz stellt einen Zusammenhang zwischen der Spannung $\sigma$ und der Dehnung $\epsilon$ her.

Merk's dir!

Das Hookesche Gesetz eignet sich besonders gut um ein elastisch verformbares Bauteil oder eine elastisch verformbare Werkstoffprobe zu beschreiben. Auch bei elastischen Verformungen bei Federsystem findet das Hookesche Gesetz Anwendung.

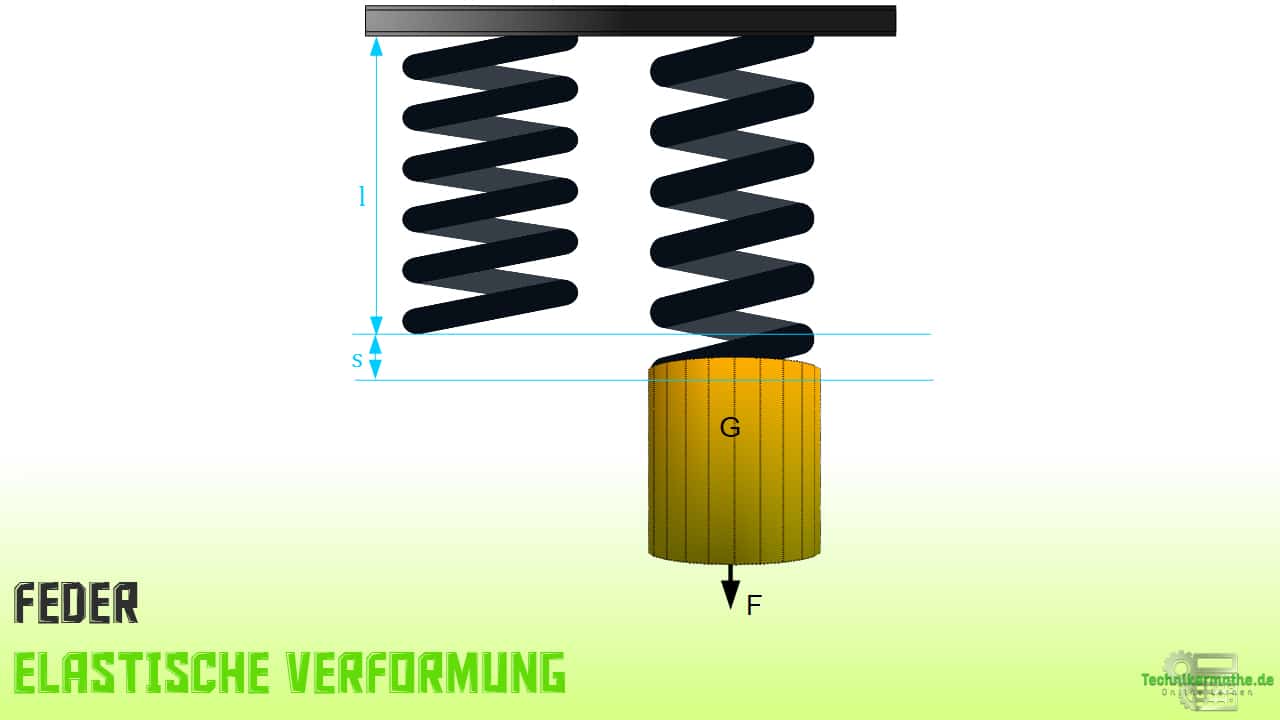
Hookesche Gesetz - Elastische Verformung einer Feder — Hookesche Gesetz – Elastische Verformung einer Feder

Als linearer Sonderfall des Elastizitätsgesetzes beschränkt sich dessen Gültigkeit auch nur auf den elastischen Bereich. Im Bereich einer plastischen Verformung findet dieses Gesetz keine Anwendung mehr.

Hookesches Gesetz – Elastizitätsmodul

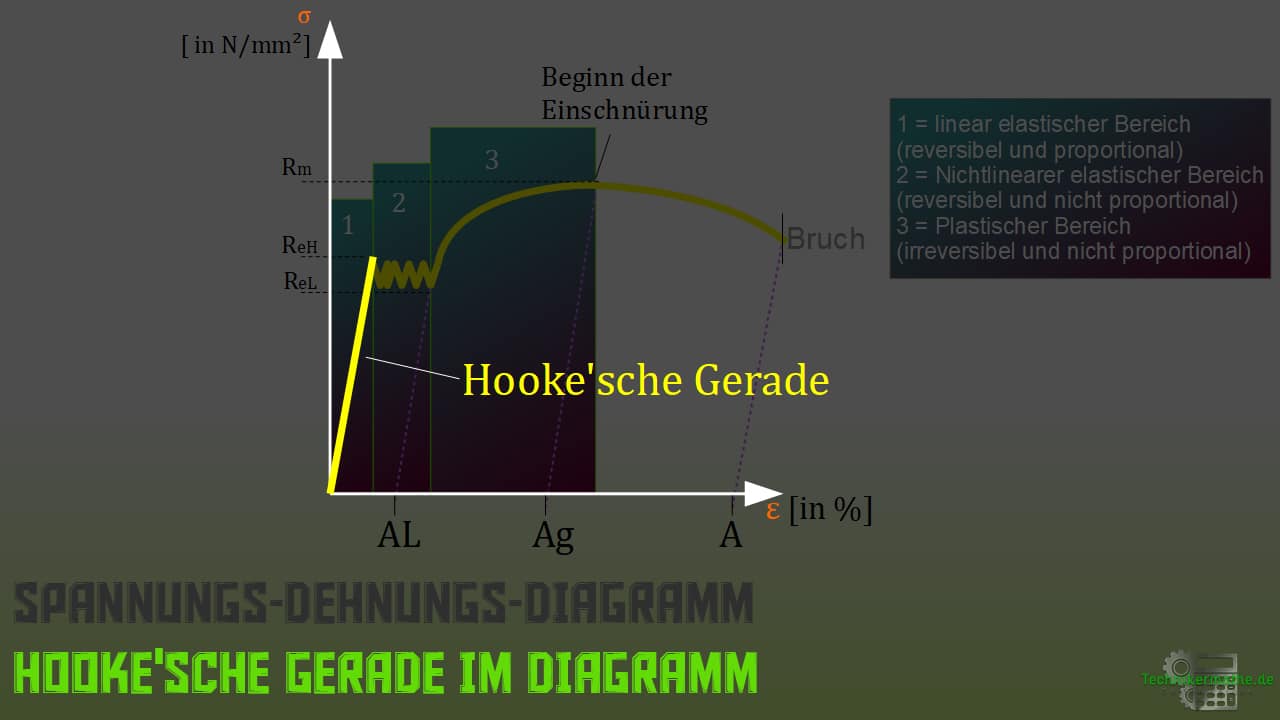
Diesen Zusammenhang und auch die anfängliche Proportionalität zwischen diesen beiden Größen haben wir bereit im Spannungs-Dehnungs-Diagramm verdeutlicht.

Das Hookesche Gesetz berücksichtigt in der Berechnungsgleichung auch den Elastizitätsmodul. Dieser ist als Proportionalitätsfaktor ist in der nächsten Gleichung dargestellt:

$\boxed{\sigma = E \cdot \epsilon }$ Elastizitätsmodul

Kennzahlen

$\boxed{ \sigma = }$ Spannung

$\boxed{ E = }$ Elastizitätsmodul

$\boxed{ \epsilon = }$ Dehnung

undefiniert

Erinnere dich...

Die Ausgangsgleichung für die Spannung und Dehnung sind:

$\boxed{ \sigma = \frac{F}{S_0}}$

$\boxed{ \epsilon = \frac{\Delta L}{L_0} }$

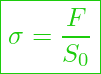
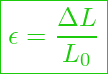
Hookesche Gerade – Elastizitätsmodul

Der Elastizitätsmodul ist im elastischen Bereich des Spannungs-Dehnungs-Diagramm die Steigung der Hooke’schen Geraden. Es handelt sich um eine konstante, werkstoffabhängige Größe.

Merk's dir!

“Der Elastizitätsmodul gilt sowohl bei einer Zug- als auch Druckbeanspruchung gleichermaßen.”

Möchte man den E-Modul berechnen so muss lediglich die Gleichung nach E aufgelöst werden:

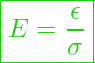$\boxed{ E =\frac{ \epsilon}{\sigma} }$ E-Modul

Kennzahlen

$\boxed{ E = }$ Elastizitätsmodul

$\boxed{ \epsilon = }$ Dehnung

$\boxed{ \sigma = }$ Spannung

Unter Verwendung der Ausgangsgleichungen für die Spannung und Dehnung ändert sich die Gleichung für den E-Modul zu:

$\boxed{ E = \frac{F \cdot L_0}{S_0 \cdot \Delta L} }$

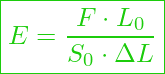
Kennzahlen

$\boxed{ E = }$ Elastizitätsmodul

$\boxed{ L_0 = }$ Anfangslänge des Stabes

$\boxed{ S_0 = }$ Anfangsquerschnitt des Stabes

$\boxed{ F = }$ Zugkraft oder Druckkraft

$\boxed{ \Delta L = }$ Verlängerung des Stabes

Übersicht E-Module (Elastizitätsmodule) verschiedener Werkstoffe

Der E-Modul variiert zwischen den unterschiedlichen Werkstoffen sehr stark. Diese Unterschiede haben wir dir nachfolgend aufgezeigt:

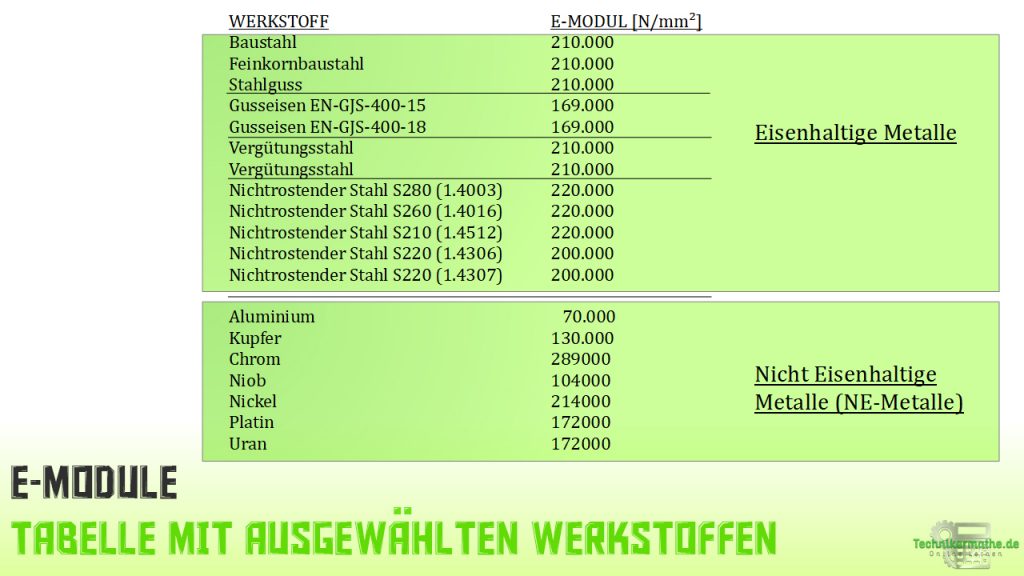
Hookesches Gesetz - Elastizitätsmodule — Hookesches Gesetz – Elastizitätsmodule

Nachfolgend noch mal als Liste mit gleichen und weiteren E-Modulen:

Werkstoff = E-Modul
Diamant E-Modul = $\boxed{ 1.200 GPa (10^3 N/mm²)}$
Wolframcarbid E-Modul = $\boxed{720 GPa (10^3 N/mm²)}$
Molybdän E-Modul = $\boxed{ 460 GPa (10^3 N/mm²) }$
Stahl E-Modul = $\boxed{210 GPa (10^3 N/mm²) }$
Kupfer E-Modul = $\boxed{ 130 GPa (10^3 N/mm²)}$
Titan E-Modul = $\boxed{ 110 GPa (10^3 N/mm²) }$
Gusseisen E-Modul = $\boxed{ 90 GPa (10^3 N/mm²)}$
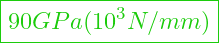
Gold E-Modul = $\boxed{ 78 GPa (10^3 N/mm²) }$
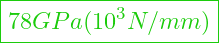
Aluminium E-Modul = $\boxed{ 70 GPa (10^3 N/mm²)}$
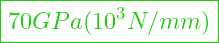
Glas E-Modul = $\boxed{ 60 GPa (10^3 N/mm²) }$
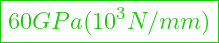
Porzellan E-Modul = $\boxed{ 55 GPa (10^3 N/mm²)}$
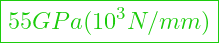
Beton E-Modul = $\boxed{ 20 GPa (10^3 N/mm²) }$
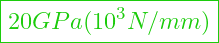
Holz E-Modul = $\boxed{ 10 GPa (10^3 N/mm²) }$
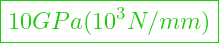
PVC E-Modul = $\boxed{ 3,5 GPa (10^3 N/mm²) }$
Gummi E-Modul = $\boxed{ 1 GPa (10^3 N/mm²)}$

wie gehts weiter?

Nachdem du jetzt gut geschult bist zum Thema Hookesches Gesetz, behandeln wir in der folgenden Lerneinheit die unterschiedlichen Brucharten.

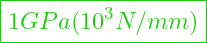
Was gibt es noch bei uns?

Finde die richtige Schule für dich!

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe.de?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Interaktive Übungsaufgaben

Quizfrage 1

Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?

Auszüge aus unserem Kursangebot

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++