(WT3-20) – Spannungs-Dehnungs-Diagramm [Prüfungsorientierte Vorstellung]

In diesem Lerneinheit erklären wir dir ausführlich das Spannungs-Dehnungs-Diagramm.

Für ein optimales Verständnis erfolgt eine genaue Erklärung des Diagramms und eine anschließende Vorstellung der einzelnen Größen inklusive Formeln.

Mehr zu diesem Thema und der Werkstofftechnik findest du im Kurs: WT3-Werkstoffprüfung

Was ist das Spannungs-Dehnungs-Diagramm?

Definition

Spannungs-Dehnungs-Diagramm?

Das Spannungs-Dehnungs-Diagramm ist eine grafische Darstellung, die den Zusammenhang zwischen Spannung ( $\sigma$ ) und Dehnung ( $\epsilon$ ) eines Werkstoffes während eines Zugversuchs zeigt. Es liefert Informationen über das mechanische Verhalten eines Materials, wie elastische und plastische Verformung, Fließgrenze, Zugfestigkeit und Bruchdehnung.

Spannungs-Dehnungs-Diagramm – Grundlagen

Merk’s dir!

“Im Spannungs-Dehnungs-Diagramm stellt man die Spannungs-Dehnungs-Kurve dar.”

Stellvertretend für unterschiedliche Kurvenverläufe ist in der nachfolgenden Abbildung die Spannungs-Dehnungs-Kurve im Spannungs-Dehnungs-Diagramm für einen weichen Stahl dargestellt.

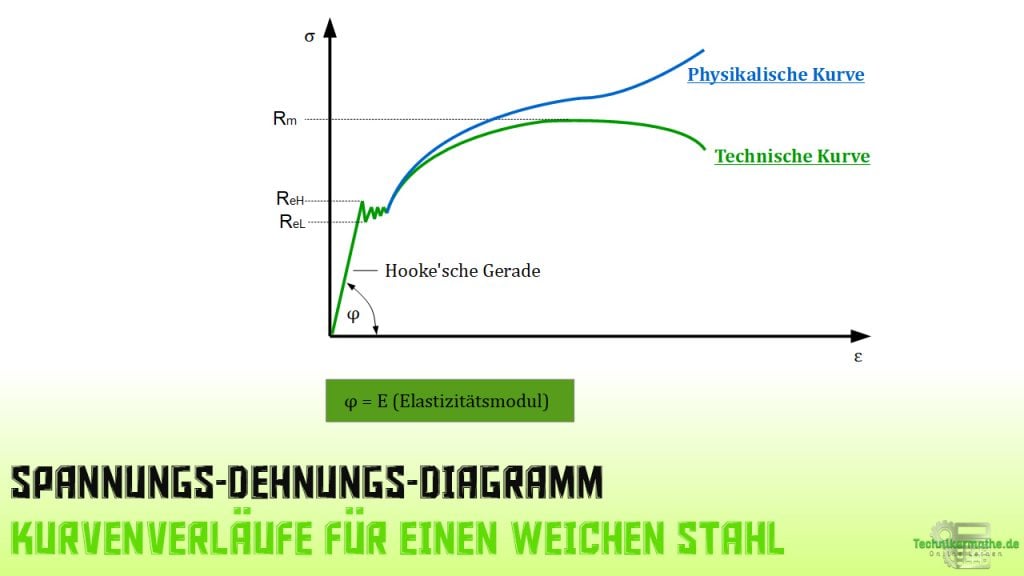
Für jeden Werkstoff existiert ein individuelles Spannungs-Dehnungs-Diagramm. Viele Werkstoffe haben einen Kurvenverlauf, welcher der obigen Abbildung entspricht. Andere Werkstoffe hingegen haben einen Kurvenverlauf bei dem kein Fließbereich vorliegt, sondern in direkte Übergang zwischen der elastischen und plastischen Verformung.

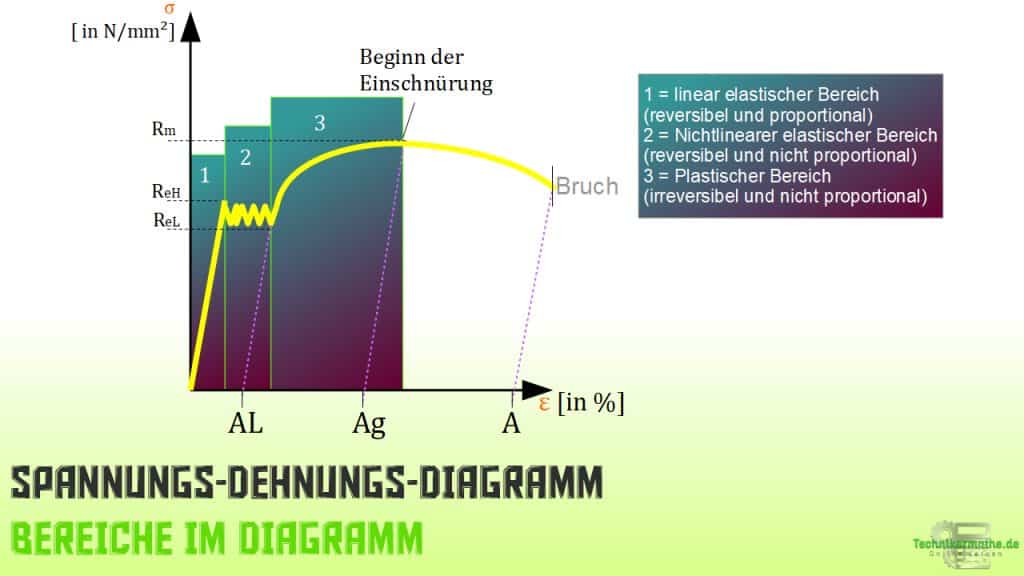
Spannungs-Dehnungs-Diagramm – Bereiche

Innerhalb des Spannungs-Dehnungs-Diagramms lassen sich unterschiedliche Bereiche ausmachen.

Linear elastischer Bereich: Zu Beginn des Kurvenverlaufs befinden wir uns im linear-elastischen Bereich. Diesen Bereich kennzeichnet, dass die Dehnung direkt proportional zur Spannung verläuft und die Dehnung sich nach Wegnahme der Spannung vollständig zurückbildet.
Nichtlinear-elastischer Bereich: Daran schließt sich der nichtlinear-elastische Bereich an. Hier verläuft die Dehnung nicht mehr proportional zur Spannung (überproportional) jedoch bildet sich auch hier die Dehnung vollständig zurück sofern die Spannung entfernt wird.
Fließbereich: Im Fließbereich kommt es bereits zu einer plastischen Verformung. Jedoch schwanken die Spannungswerte trotz zunehmender Dehnung.
Materialverfestigungsbereich: Aufgrund von Vorgängen innerhalb der Gitterstruktur kommt es zum Abflachen der Kurve trotz zunehmender Spannung.
Einschnürungsbereich: In der Gitterstruktur haben sich bereits Hohlräume gebildet und es beginnt die Einschnürung in der Probenmitte. Das kennzeichnet sich dadurch, dass die Kurve abfällt. Für eine weitere Dehnung der Probe ist nun immer weniger Spannung erforderlich. Dieser Vorgang setzt sich bis zum Bruch fort.

Spannungs-Dehnungs-Diagramm - Bereiche im Diagramm — Spannungs-Dehnungs-Diagramm

Vorgänge und Gleichungen

Zu Beginn des Versuches ist die Probe (Zustand 1) unbelastet und die Dehnung ist 0.

Mit ansteigender Spannung nimmt die Dehnung zuerst linear zu. Noch befinden wir uns im Bereich der elastischen Formänderung. Das bedeutet im Falle einer Wegnahme der Belastung, fällt die Dehnung wieder auf den Wert 0 zurück.

Diesen Kurvenbereich mit einer elastischen Formänderung bezeichnet man als Hooke’sche Gerade. Alternativ spricht man auch von der Federkennlinie des Probenstabes.

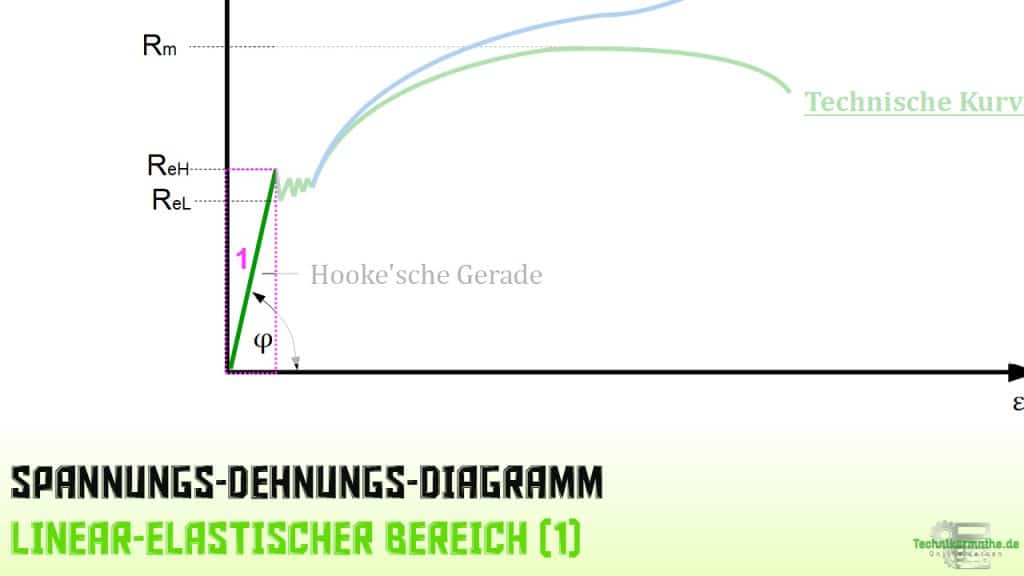
Spannungs-Dehnungs-Diagramm - Linear elastischer Bereich — Spannungs-Dehnungs-Diagramm

Die Steigung dieser Geraden nennt man den Elastizitätsmodul (kurz E-Modul) des geprüften Werkstoffes. Formal ergibt sich das wie folgt:

E-Modul – Formel

E-Modul

$E = tan \varphi = \frac{\Delta \sigma}{\Delta \epsilon}$

Kennzahlen

$E =$ E-Modul

$\varphi =$ Steigungswinkel

$\Delta \sigma =$ Änderung der Spannung

$\Delta \epsilon =$ Änderung der Dehnung

Merk’s dir!

Ein typischer Wert für Stahl ist E = 210 GPa. Das GPA steht hier für Gigapascal.

Die Probe (Zustand 2) liegt bereits im Fließbereich.

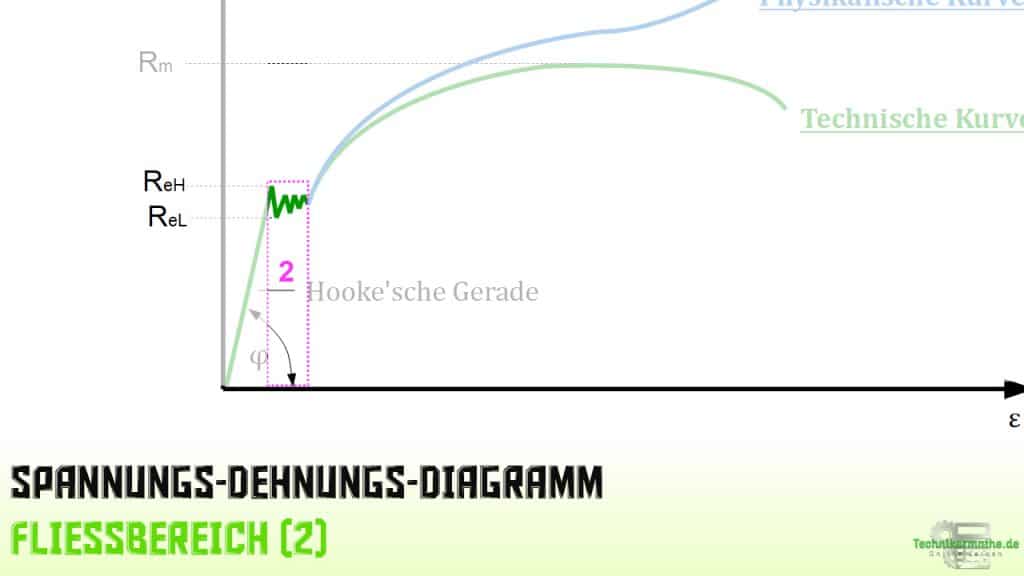
Spannungs-Dehnungs-Diagramm - Fließbereich — Spannungs-Dehnungs-Diagramm – Fließbereich

Das Fließen des Werkstoffes der Probe beginnt, sobald die Zugspannung weiter zunimmt. Ab diesem Zeitpunkt sind die Spannungs-Dehnungs-Kurve in die Hooke’sche Gerade nicht mehr deckungsgleich. Wir bezeichnen diesen Punkt auf der Kurve mit $R_{eH}$ . Es handelt sich um die obere Streckgrenze (H = higher).

Ab diesem Zeitpunkt bleibt auch bei einer Entlastung (Wegnahme der Zugspannung) eine dauerhafte Dehnung. Du kennst diese bereits als plastische, bzw. irreversible Verformung.

Dass hier in diesem Bereich eine Unstetigkeit besteht, wird durch den zackigen Verlauf der Kurve deutlich. Je nach Werkstoff fällt dieser Fließbereich stärker oder schwächer aus.

Die kleinste Spannung, die hier auftritt, ist mit $R_{eL}$ die untere Streckgrenze (L = lower).

Hier ist es irgendwie anders…

Liegt ein Werkstoff vor, bei dem keine ausgeprägte Streckgrenze vorliegt, so ermittelt man stattdessen die Dehngrenze $R_p$ . Hier liegt dann ein stetiger Übergang vom elastischen in den plastischen Bereich vor.

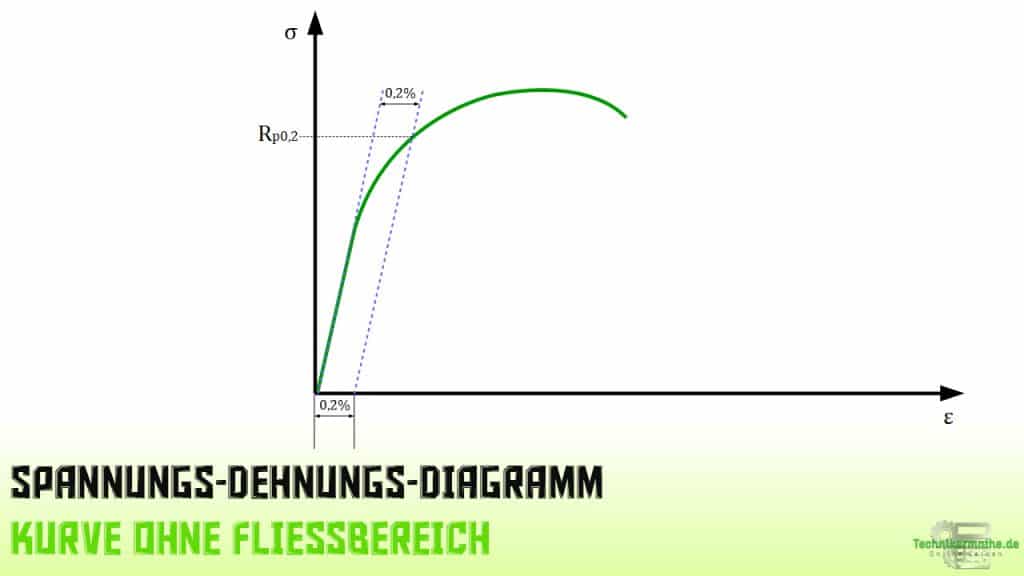
Spannungs-Dehnungs-Diagramm ohne Fließbereich

Die Dehngrenze gibt die Spannung bei einer bleibenden Dehnung an. Dabei entspricht der Zahlenwert der Dehnung in Prozent.

Steht dort $R_{p0,2}$ so handelt es sich um die 0,2 % Dehngrenze.

Steht dort hingegen $R_{p0,01}$ so handelt es sich um die 0,01 % Dehngrenze.

Letztere wird auch als technische Elastizitätsgrenze bezeichnet.

Zugfestigkeit – Formeln

Die Probe (Zustand 3) ist infolge des fortwährenden Streckens kaltverfestigt. Dabei besteht die Gesamtdehnung aus einem elastischen und einem plastischen Anteil.

Spannungs-Dehnungs-Diagramm - Kaltverfestigung, Materialverfestigung — Spannungs-Dehnungs-Diagramm – Kaltverfestigung, Materialverfestigung

Den maximale Spannungswert, welcher hier erreicht wird (also der Hochpunkt der Kurve), bezeichnet man als Zugfestigkeit $R_m$ .

Die Zugfestigkeit ist der Spannungswert, welcher sich aus der auf den Anfangsquerschnitt $S_o$ bezogenen Höchstlast ergibt.

Zugfestigkeit

Formal berechnet sich die Zugfestigkeit wie folgt:

$R_m = \frac{F_m}{S_o}$

Kennzahlen

$R_m =$ Zugfestigkeit

$F_m =$ Maximalkraft

$S_0 =$ Ausgangsquerschnitt

Bruchdehnung – Formel

Die Probe (Zustand 4) zeigt erste Einschnürungen. Die Kurve fällt folglich ab. Am Ende steht der Bruch des Probenstabes.

Spannungs-Dehnungs-Diagramm - Einschnürung — Spannungs-Dehnungs-Diagramm – Einschnürung

Mit Eintreten des Bruchs steht auch die Bruchdehnung $A$ fest. Sie ist die bleibende Dehnung und wird in Prozent angegeben.

Man ermittelt diese, indem man im ersten Schritt die beiden Probenstücke gerade zusammenlegt und anschließend die Gesamtlänge mit $L_U$ ermittelt.

Anschließend setzt man diese in ein Verhältnis mit der Ausgangslänge $L_o$ .

Bruchdehnung

Formal sieht das dann wie folgt aus:

$A = \frac{L_U - L_0}{L_o} \cdot 100$

Kennzahlen:

$A =$ Bruchdehnung

$L_U =$ Gesamtlänge nach Bruch

$L_0 =$ Ausgangslänge

Dehnungsverlauf der Bruchdehnung

In der nächsten Abbildung siehst du den Dehnungsverlauf für die Bruchdehnungen eines kurzen (A5) und eine langen (A10) Probenstabes.

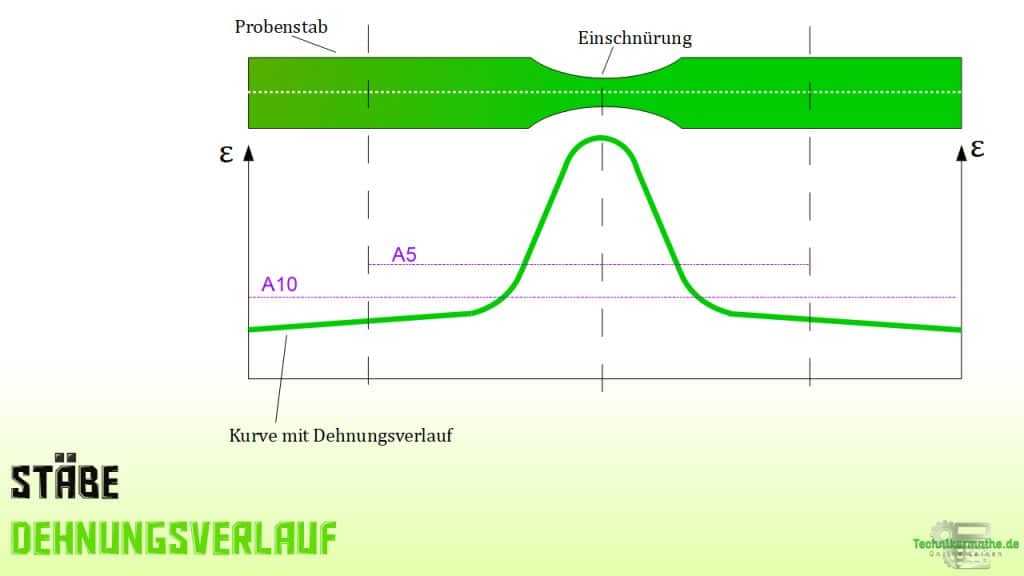
Es zeigt sich deutlich, dass die Gleichmaßdehnung beim langen Stab auch stärker ausfällt.

Daher muss in Vergleichen auch immer angegeben werden, welche Form von Probenstab für den Versuch verwendet wurde.

Brucheinschnürung – Formeln

Merk’s dir!

Gelegentlich wird die Brucheinschnürung Z als Messgröße für das Formänderungsvermögen eines metallischen Werkstoffes herangezogen.

Es handelt sich bei dieser Größe im die bleibende Querschnittsverringerung $\Delta S$ in Bezug auf den Ausgangsdurchmesser $S_0$

Brucheinschnürung

Formal errechnet sich dieser mit:

$Z = \frac{S_0 - S_U}{S_0} \cdot 100 = \frac{\Delta S}{S_0} \cdot 100$

Kennzahlen

$Z =$ Brucheinschnürung

$S_0 =$ Anfangsquerschnitt

$S_U =$ Querschnitt nach Bruch

$\Delta S =$ Querschnittsminderung

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was zeigt das Spannungs-Dehnungs-Diagramm?

Das Spannungs-Dehnungs-Diagramm zeigt, wie sich ein Material unter Zugbelastung verhält, von der elastischen Verformung bis hin zum Bruch.

2. Welche Bereiche gibt es im Spannungs-Dehnungs-Diagramm?

Die Hauptbereiche sind der linear-elastische Bereich, der nichtlinear-elastische Bereich, der Fließbereich, der Materialverfestigungsbereich und der Einschnürungsbereich.

3. Was ist der E-Modul und wie wird er berechnet?

Der Elastizitätsmodul ( $E$ ) ist ein Maß für die Steifigkeit eines Materials und wird berechnet als:

$E = \frac{\Delta \sigma}{\Delta \epsilon}$

4. Was ist der Unterschied zwischen Fließgrenze und Dehngrenze?

Fließgrenze: Punkt der plastischen Verformung mit Spannungsfluktuationen 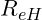$R_{eH}$ und $R_{eL}$ .
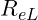Dehngrenze: Spannung bei dauerhafter Dehnung ohne Fließbereich (z. B. $R_{p0,2}$ ).

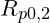5. Wie unterscheidet sich die Bruchdehnung von der Brucheinschnürung?

Bruchdehnung (A): Bleibende Längenänderung der Probe in Prozent.
Brucheinschnürung (Z): Bleibende Querschnittsverringerung in Prozent.

Zusammenfassung

Grundlagen: Das Spannungs-Dehnungs-Diagramm visualisiert die Spannungs-Dehnungs-Kurve eines Materials. Jeder Werkstoff hat ein individuelles Diagramm.
Bereiche:
- Linear-elastischer Bereich: Proportionalität zwischen Spannung und Dehnung; reversibel.
- Nichtlinear-elastischer Bereich: Dehnung nicht proportional, aber reversibel.
- Fließbereich: Übergang zur plastischen Verformung mit Spannungsfluktuation.
- Materialverfestigungsbereich: Steigende Spannung trotz zunehmender plastischer Verformung.
- Einschnürungsbereich: Abnahme der Spannung bis zum Bruch.
Kennwerte:
- E-Modul: Steigung der Hooke’schen Geraden.
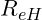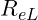- Streckgrenze $R_{eH}$ und $R_{eL}$ : Übergang elastisch zu plastisch.
- Zugfestigkeit 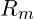$R_m$ : Maximale Spannung.
- Bruchdehnung (A): Bleibende Dehnung nach Bruch.
- Brucheinschnürung (Z): Relative Querschnittsverringerung.

In der folgenden Lerneinheit behandeln wir das Hooke’sche Gesetz und stellen wir einige E-Module vor.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++