Mehr zu diesem Thema und der Werkstofftechnik findest du im Kurs: WT3-Werkstoffprüfung
Der Dauerschwingversuch oder auch Wöhlerversuch dient zur Untersuchung des Schwingverhaltens von Bauteilen über längere Zeit als Prüfverfahren. Mit Hilfe der Wöhlerkurve und dem Smith-Diagramm kann dieser Versuch ausgewertet werden.
Dauerschwingversuch – Grundlagen
Anders als beim Zugversuch, bei welchem eine einmalige, allmählich steigende Zugbelastung untersucht wird, betrachtet der Dauerschwingversuch auch das Werkstoffverhalten eines Bauteils bei einer wiederholenden Beanspruchung. Diese Beanspruchung ist dynamisch und zeichnet sich dadurch aus, dass sie schwellend und wechselnd auftritt.
Die Kurzzeitfestigkeit wird mit dem Dauerschwingversuch nicht ermittelt.
Werden Ständer, Fundamente oder Gehäuse vorwiegend statisch belastet, so unterliegen Wellen, Zahnräder, Federn und Achsen hauptsächlich einer dynamischen Belastung.
Organisatorisches
Organisiert ist der Dauerschwingversuch (Wöhlerversuch) in der DIN50100.”
Der Dauerschwingversuch bildet die Beanspruchung von Maschinenbauteilen genauer ab, als andere Verfahren. Denn eingebaute Maschinenbauteile sind im Betrieb regelmäßig Schwingungen ausgesetzt und müssen diesen auch über einen längeren Zeitraum unbeschadet standhalten.
Die Auswertung des Versuchs erfolgt durch die Wöhlerkurve und das Smith-Diagramm (Dauerfestigkeitsdiagramm).”
Dynamische Beanspruchung
Bevor wir mit dem Versuchsaufbau starten, klären wir zunächst wodurch sich eine dynamische Beanspruchung auszeichnet.
Beinahe jedes bewegliche Maschinenbauteil ist im Betrieb einer mehr oder weniger regelmäßigen Belastung und Entlastung ausgesetzt. Dabei zeigt sich besonders, dass die wiederkehrenden Schwingungen und Erschütterungen, dazu führen, dass ein Bruch bei Betriebsspannungen auftritt, welche unterhalb der in Versuchen ermittelten Festigkeiten liegen.
In diesem Zusammenhang spricht man von dynamischen Belastungen.
Im Rahmen einer dynamischen Belastung haben, die aus dem Zugversuch ermittelten Festigkeitswerte des eingesetzten Werkstoffes keine Gültigkeit mehr und dürfen aus Gründen der Betriebssicherheit jetzt nur noch anteilig angenommen werden.
Um ein passenden Eindruck davon zu erhalten, wie stark die Festigkeitswerte bei einer schwellenden und wechselnden Belastung abfallen, möge die nachfolgende Abbildung helfen.
Dauerfestigkeit
Die Dauerfestigkeit, oder auch Dauerschwingfestigkeit, ist der maximale Spannungsausschlag um eine gegebene Mittelspannung herum, welchen ein Bauteil unbegrenzt oft aushält, ohne dabei zu brechen.
Welchen Wert ein Werkstoff hinsichtlich seiner Dauerfestigkeit annimmt, wird im Vorfeld durch Versuche (Pulsern) experimentell ermittelt und lässt sich dann auf das Verhalten des daraus hergestellten Bauteils übertragen.
Sobald diese Dauerschwingfestigkeit überschritten wird, kommt es im Zeitverlauf zur Rissen und schließlich zum Bauteilversagen des Maschinenbauteils.
Dauerbruch
Den damit einhergehenden Dauerbruch (90% der Fälle) erkennt man zumeist an seiner spezifischen Bruchfläche. Vorläufer des Dauerbruchs sind durch Verformungen ausgelöste Störungen an den Korngrenzen innerhalb der Bauteils, die dann in sich ausbreitenden Rissen münden. Wie diese Form von Bruch aussieht, ist im Vergleich zu einem Sprödbruch in der nächsten Abbildung dargestellt.
Man kann übrigens auch eine Liste von Ursachen heranziehen, welche typische Faktoren für einen Dauerbruch sind:”
- Erhöhte Schwingbeanspruchung
- Erhöhte Anzahl von Belastungsänderungen pro Minute (Schwingspielfrequenz)
- Vorliegen von Rissquellen
Die Rissquellen ergeben sich auch den bereits erwähnten Störungen an Korngrenzen aber auch durch Einlagerungen andere Werkstoffe (heterogene Werkstoffgefüge) sowie Kerben an der Bauteiloberfläche.
Innere & äußere Kerben
Einlagerungen anderer Werkstoffe, die zu einem heterogenen (ungleichmäßigen) Werkstoffgefüge führen bezeichnet man als innere Kerben. Die an der Bauteiloberfläche vorliegenden Kerben sind äußere Kerben.
Zur Gruppe der inneren Kerben zählen
- Schlacken
- Silikate sowie
- Graphitlamellen.
Zur Gruppe der äußeren Kerben zählen
- Riefen (bearbeitungsbeding)
- Bohrungen,
- Nuten,
- Gewinde sowie
- Übergänge bei Wellen (Wellenabsätze)
Gestaltfestigkeit
Besonders die äußeren Kerben stellen einen Konstrukteur vor eine besondere Herausforderung, denn somit kann nicht mehr von den Dauerfestigkeitswerten des Werkstoffes aus den Versuchen ausgegangen werden. Stattdessen gilt es zu prüfen welche Formen (eckig, rund) von äußeren Kerben am Bauteil vorliegt. Denn Kerben weisen Spannungsspitzen am Kerbgrund auf. Um hier Abhilfe zu schaffen, empfiehlt es sich die Gestaltfestigkeit zu ermitteln.
Gestaltfestigkeit wird als die Dauerfestigkeit von vollständigen Bauteilen in Berechnungen aufgenommen. Ein vollständiges Bauteil kann eine Feder oder eine Schraube sein. Berücksichtigt werden hier alle herstellungsbedingten äußeren Kerben.
Dennoch ist es möglich durch geeignete konstruktive Maßnahmen an den Bauteilen das Dauerschwingverhalten positiv zu beeinflussen. Dies gelingt z.B. durch Abrunden von kantigen Absätzen oder durch eine Randschichthärtung der Bauteiloberfläche. Letzteres erzeugt Druck-Eigenspannungen in der Randzone, die Spannungen durch äußere Belastungen kompensieren.
Prüfung – Ablauf
Nach der ganzen Vorarbeit kommen wir nun endlich zum Dauerschwingversuch. Bei diesem Versuch werden die Bauteile oder stellvertretend Proben aus den verwendeten Werkstoffen zumeist über längere Zeiträume schwingend beansprucht.
Prüfmaschinen
Einer der bekanntesten Vertreter von Prüfmaschinen ist der Zug-Druck-Pulser.
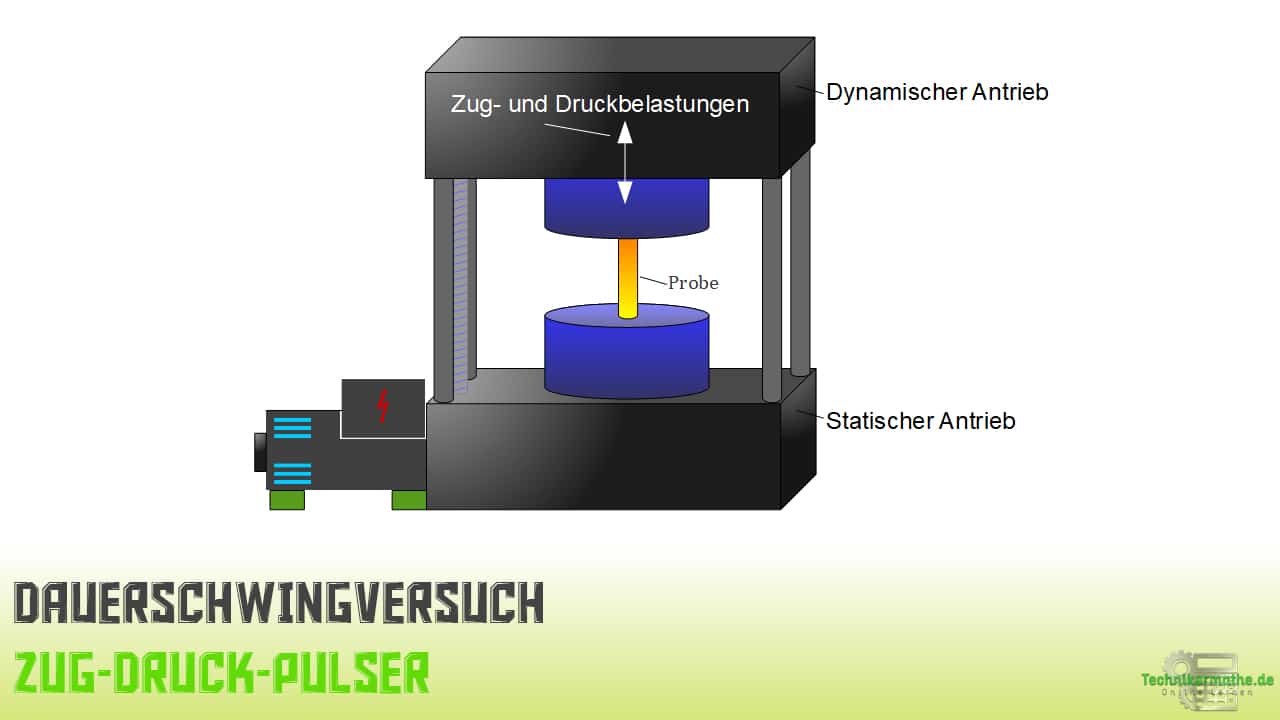
Diese Maschine verursacht eine sich zeitlich ändernder Zug-Druck-Belastung am Bauteil mit Hilfe einer rotierenden Unwucht.
Eine Alternative stellt die Umlaufbiegemaschine dar. Hier werden Proben (zylindrisch) eingespannt und auf Biegung beansprucht. Zeitgleich wird eine rotierende Bewegung erzeugt. Als Ergebnis erhält man hier einen Biegemomentverlauf.
Neben den herkömmlichen Belastungsarten wie Zug, Druck sowie Biegung können auch Schub und Verdrehung, als komplexe Bauteilbeanspruchungen nachgestellt werden.
Spannungs-Zeit-Kurve
Nach Abschluss der Prüfung liegt eine Spannungs-Zeit-Kurve vor.
Die Größen, welche sich aus dieser Kurve ablesen lassen, sind nachfolgend aufgelistet:
= Oberspannung: Größter Spannungswert je Schwingspiel
= Unterspannung: Kleinster Spannungswert je Schwingspiel
= Mittelspannung: Mittelwert aus Oberspannung und Unterspannung
= Amplitude: Spannungsausschlag
= Schwingbreite der Spannung
Aus diesen Werten lassen sich schließlich noch Ausprägungen der Schwell- und Wechselbereiche ermitteln:
= Zug-Schwellbereich, wobei 
und 
positive Vorzeichen besitzen.
= Wechselbereich, wobei und unterschiedliche Vorzeichen aufweisen.
= Druck-Schwellbereich, wobei und negative Vorzeichen besitzen.
In der nachfolgenden Abbildung sind diese Bereiche noch ein mal dargestellt:
Wie du vielleicht schon gemerkt hast, ist es die Lage der Mittelspannung, die darüber entscheidet in welchem Bereich wir uns befinden.
Wöhlerversuch
Ausgehend von einer Schwingbeanspruchung stellt der Wöhlerversuch eine besonders gute Variante des Dauerschwingversuchs dar. Hier werden maximal 12 Proben einer unterschiedlichen Schwingbeanspruchung ausgesetzt.
August Wöhler war einer der ersten, die ihre Arbeit der dynamischen Beanspruchung von Bauteilen widmete. Er fand im Zusammenhang mit Bruchereignissen im Schienenfahrzeugbau heraus, dass es die schwingenden, wiederholenden Beanspruchungen waren, die ein Bauteilverfahren herbeigeführt haben. Und das obwohl die Beanspruchungen unterhalb der maximal zulässigen Beanspruchung für den statischen Fall lagen.
Anforderung & Zweck
“Wichtig ist hier, dass unabhängig davon wie viele Proben letztlich untersucht werden, diese alle die gleiche Ausprägung haben. Soll heißen: Form und Oberflächenbeschaffenheit müssen identisch sein.”
Sobald der Versuch startet werden mit Hilfe eines Zählwerks die Schwingspielzahlen gezählt. Dieser Vorgang läuft so lange bis der Probenbruch eintritt. Ziel ist es jedoch nicht den Probenbruch zu erzeugen, sondern die Beanspruchung zu ermitteln bei welcher kein Bruch eintritt.
Sowohl die Mittelspannung 
als auch die Spannungsamplitude 
werden bis zum Eintreten des Bruchs bei jeder Probe konstant gehalten.
Wöhlerkurven – Auswertung der Prüfergebnisse
Als Ergebnis des Wöhlerversuchs erhält man eine Wöhlerkurve, die uns Aufschluss darüber gibt, wie viele Lastwechsel ein Bauteil aushält bevor es bricht. Die Beanspruchung im Verlauf erfolgt sinusförmig, so wie du es oben bereits gesehen hast.
Für jede Probe wird die Spannungsamplitude über der zugehörigen Bruchlastspielzahl 
(B = Bruch) aufgetragen. Daraus ergibt sich dann die Wöhlerdiagramm mit Wöhlerkurve.
Generell untergliedert man den gesamten Kurvenverlauf der Wöhlerkurve in drei Bereiche:
- Kurzzeitfestigkeit = In diesem Bereich ist von einer Werkstoffschädigung auszugehen (= Bereich der Überbeanspruchung mit Bauteilschädigung)
- Langzeitfestigkeit = In diesem Bereich wird die Schwingbeanspruchung mit erhöhtem Spannungsausschlag durch die Schwingspielzahl begrenzt. (= Bereich der Überbeanspruchung ohne Bauteilschädigung)
- Dauerfestigkeit = In diesem Bereich ist eine Schwingbeanspruchung zeitlich unbegrenzt möglich. Es ist keine Werkstoffschädigung zu erwarten. (= Bereich der Beanspruchung unterhalb der Dauerfestigkeit ohne Bauteilschädigung)
Bei einer Schwingspielzahl von 
stellt sich zumeist ein waagerechter Verlauf der Wöhlerkurve ein. Diese entspricht ungefähr 
.
Eine Wöhlerkurve wie im obigen Bild ergibt sich nach statistischer Auswertung von mehreren Proben, welche mit identischer Spannungsamplitude geprüft wurden. Eine statistische Auswertung ist zwingend erforderlich, denn selbst bei identischer Spannungsamplitude können sehr starke Streuungen in der Bruchlastspielzahl auftreten.
Schadenslinie – Verfahren von French
Die Schadenslinie im Wöhlerdiagramm begrenzt für alle Schwingbeanspruchungshöhen über der Dauerfestigkeit 
die Lastspielzahl. Diese begrenzte Lastspielzahl hält ein Bauteil aus ohne dass des zur Schädigung des Werkstoffes kommt.
Dabei wird die Schadenslinie nicht einfach frei gewählt, sondern ist im Vorfeld nach dem Verfahren von French ermittelt worden. Hierbei setzt man mehrere Proben bei gleicher Belastung, die Oberhalb der Dauerfestigkeit liegt unterschiedlichen Lastspielzahlen aus, die jedoch unterhalb der Bruch-Lastspielzahl liegen.
Kritik an der Aussagekraft
Die Wöhlerkurve aus dem Wöhlerversuch (Dauerschwingversuch) kann ausschließlich zur Auswertung eines Dauerschwingversuches genutzt werden, da es sich lediglich auf die Mittelspannung bezieht.
Abhilfe, schafft hingegen das im nachfolgenden behandelte Smith-Diagramm als Dauerfestigkeitsdiagramm.
Nachdem du jetzt den Dauerschwingversuch als eine weitere Variante der Prüfverfahren kennengelernt hast und jetzt weißt wofür die Wöhlerkurve dient, stellen wir dir im kommenden Kursabschnitt in diesem Zusammenhang das Dauerfestigkeitsdiagramm (Smith-Diagramm) vor, welcher nach einem anderen Prinzip erstellt wird.
Was gibt es noch bei uns?
Tausende interaktive Übungsaufgaben
Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Das erwartet dich!
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Auszüge aus unserem Kursangebot!
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++
Oder direkt >> Mitglied << werden und >> Zugriff auf alle 26 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 7,40 EUR/Monat
++ Besser geht’s nicht!! ++
Technikermathe.de meets Social-Media
Dein Technikermathe.de-Team
