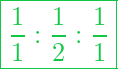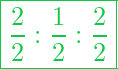Mehr zu diesem Thema und der Werkstofftechnik findest du im Kurs: WT3-Werkstoffprüfung
Die Gittereigenschaften geben uns Aufschluss hinsichtlich des Aufbaus eines Kristallgitters. Dabei unterscheiden wir verschiedene geometrische Eigenschaften bei der Beschreibung.
Gittereigenschaften – Gitterrichtungen
“Die Gitterrichtungen lassen sich mit Hilfe der Gittergeraden beschreiben.”
Wie du bereits, weißt handelt es sich dabei um die Geraden, auf denen sich in regelmäßigen Abständen Atome befinden. Es handelt sich um eine eindimensionale Betrachtung der Elementarzelle.
Die Gittergeraden können mit Hilfe von Vektoren beschrieben werden. Diese Vektoren zeigen vom Koordinatenursprung bis zum Mittelpunkt des betrachteten Atoms.
Für die Koordinaten der Gittergeraden nutzt man immer ganzzahlige Angaben. Aus diesem Grund spricht man auch von teilerfremden Koordinaten.
Zur Verbildlichung der Vorgehendesweise betrachten wir nun stellvertretend für die anderen Gittertypen das orthorhombische Gitter:
Methode
Wir kennen ja bereits die Geometrie diese Gittertyps als eine der Gittereigenschaften. Es ist angegeben mit:
sowie
Mit Hilfe von Richtungsindizes können wir die Gitterrichtung genau beschreiben.
Darüberhinaus berücksichtigen wir die Abmessungen der Elementarzelle
sowie
Die Einheitsvektoren mit der Länge 1
Mit Hilfe dieser Angaben können wir nun die Position des Gitteratoms durch die Resultierende
bestimmen.
Dabei gilt:
In unserem Fall wäre dies:
Die Einzelnen Summanden werden nicht miteinander addiert. Stattdessen tauchen sie lediglich als Zahlenfolge auf.
Beispiele 1 – 3
Damit du ein Gefühl davon bekommst, wie mit diesen Angaben umzugehen ist, folgen nun 3 Beispiele:
Fall 1: , so ist
und
Die Angabe der Koordinaten ist dann folgende: [111]
Merke: Dieser Fall ist sehr einfach, da es keine Brüche oder sonstiges gibt.
Fall 2: 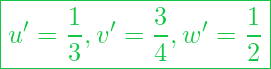
und
Die Angabe der Koordinaten ist dann folgende: [496]
Ergänzung zu Beispiel 2: Falls du dich jetzt fragst wie die Zahlen der Koordinaten-Angabe zustande kommen, dann folgt hier die Lösung: Alle Nenner benötigen den gleichen Wert und der erste gemeinsame Teiler von ist 12. Daher müssen wir die Nenner entsprechend gleichnamig machen. Dieser Multiplikator muss dann mit dem Wert von dem Zähler multipliziert werden und wir haben dann unsere Angabe.
- 4 ergibt sich auch aus der Multiplikation des Bruchs mit dem Wert
um den gleichen Nenner für
zu erhalten wie für
. Da im Zähler von
nur eine
steht wird daraus der Wert
- 9 ergibt sich ebenfalls aus der Multiplikation des Bruchs mit dem Wert
um den gleichen Nenner für
zu erhalten wie für
. Da im Zähler von
bereits eine
steht wird daraus der Wert
- 6 ergibt sich auch aus der Multiplikation des Bruchs mit dem Wert
um den gleichen Nenner für
zu erhalten wie für
. Da im Zähler von
nur eine
steht wird daraus der Wert
Fall 3: 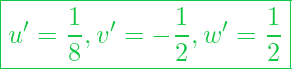
und
Die Angabe der Koordinaten ist dann folgende: []
Ergänzung zu Beispiel 3: Das Prinzip ist das gleiche wie im Fall 2. Der Unterschied ist hier, dass einer der Werte negativ ist mit . Diesen Umstand berücksichtigen wir bei der Koordinatenangabe nicht mit einem Minuszeichen, sondern mit einen Strich über dem entsprechenden Zahlenwert.
In allen Fällen geben wir die reziproken Werte an! Denn sobald alle Werte auf den Hauptnenner gebracht wurden, können wir die Brüche entfernen, da diese keinen Einfluss auf das Zahlenverhältnis besitzen.
Gittereigenschaften – Würfelkanten
Die Würfelkanten als Gittereigenschaften werden im kubischen Gitter ebenfalls bestimmt. Hier könnte folgende Angabe vorliegen:
[100], [010], [001]Die Angabe der Gesamtheit der Würfelkanten wäre dann folgende <100>.
Damit wird gekennzeichnet, dass alle aus kristallographischer Sicht gleichwertig sind.
Gittereigenschaften – Millersche Indizes
“Jetzt gehen wir von der eindimensionalen Beschreibung über zur zweidimensionalen Beschreibung von Elementarzellen, indem wir nun die Ebenen von Gittern bestimmen.”
Diese Ebenen können in das Gitter gelegt werden und darauf befinden sich dann entsprechend die Atome.
Aus diesem Grund spricht man auch von Atomebenen oder halt von Netzebenen.
Miller’sche Indizes – Überblick
Zur einheitlichen Erfassung der Gitter und um eine Vergleichbarkeit zu ermöglichen, nutzt man die Miller’schen Indizes .
Wir starten damit, dass wir ein räumliches Koordinatensystem in das Gitter legen. Anschließend setzen wir die Bereiche, welche die Ebene von den Achsen abtrennt, zueinander in ein Verhältnis.
Dabei verzichten wir auf die herkömmlichen Angaben wie cm, mm oder nm. Stattdessen verwenden wir Gitterparameter.
Bitte verzichte darauf den Achsenursprung in die zu induzierende Ebene zu legen. Tust du dies doch, so besteht die Gefahr, dass du Abschnitte der Achsen erhältst, die den Wert 000 aufweisen. Und so können wir keine Verhältnisse erzeugen.
Also achte darauf, dass du die indizierende Fläche oder umgekehrt das Achsenkreuz parallel zur Ausgangsposition verschiebst.
Wie bei den Gittergeraden verwenden wir ebenfalls die reziproken Werte, denn nachdem wir die Werte auf einen gemeinsamen Nenner gebracht haben, können wir letzteren streichen, da dieser ja keinen Einfluss mehr auf das Zahlenverhältnis haben.
Methode – Grundlagen
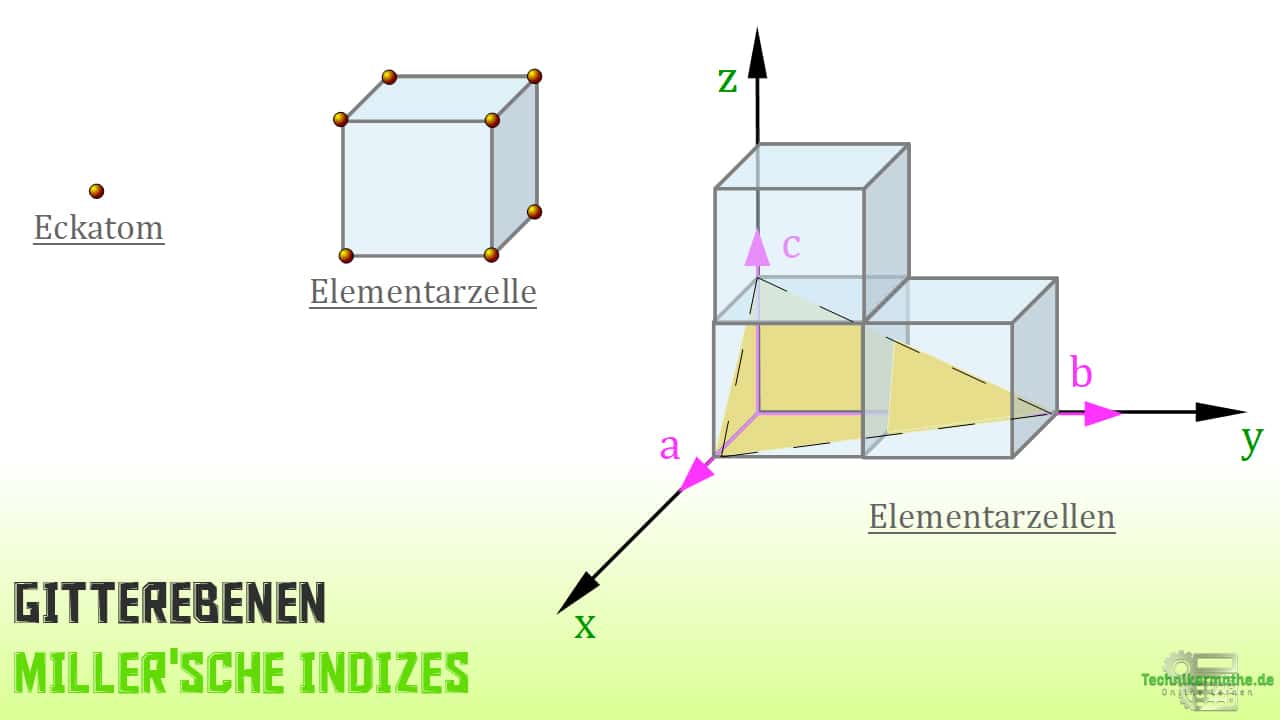
Für ein besseres Verständnis, schauen wir uns die nachfolgende Abbildung genauer an. Hier haben wir die Ebene so gelegt, dass zwei Elementarzellen teilweise indiziert werden.

Der Abbildung können wir entnehmen, dass mit a,b,c drei Gitterparameter gegeben sind, die die Achsenabschnitte beschreiben. Man bezeichnet sie als Ableitungskoeffizienten.
Zur Lösung verwenden wir ein Schema, welches sich in insgesamt 7 Schritte unterteilt.
- Erfassung der Ableitungskoeffizienten: Für unseren Fall ergeben sich die folgenden Koeffizienten in „alphabetischer“ Reihenfolge:
- Die Zahlen setzen wir jetzt einfach in ein Verhältnis zueinander:
- Anschließend bilden wir die reziproken Werte:
- Jetzt überlegen wir, welcher der 1. gemeinsame Nenner ist. In unserem Fall wäre das jetzt der Wert 2:
- Wie in den Malen davor, streichen wir einfach Nenner bei allen Werten:
- Dies Werte setzen wir jetzt in runde Klammern, die Verhältnispunkte lassen wir dabei weg.
- Jetzt sind wir am Ziel und haben die Angabe der Miller’scher Indizes (hkl) mit (212)
Falls es dir gerade entfallen ist, die Gitterebenen werden immer mit runden Klammern angegeben, die Gitterrichtungen hingegen mit eckigen Klammern.
Und wenn auschließlich eine Ebenenart ermittelt, bzw. dargestellt werden soll, dann werden die Miller’schen Indizes in geschweifte Klammer gesetzt.
- Gitterebenen: (…)
- Gitterrichtungen: […]
- 1 Ebenenart: (…)
Das kubische Kristallsystem ist ein besonderes System, denn hier stimmen Gitterrichtungen und Gitterebenen überein.
Anders verhält es sich beim hexagonalen Kristallsystem. Denn hier werden die Indizes der Richtungen und der Ebenen mit vier statt drei Ziffern angegeben.
Gitterrichtungen: Hier kommt das Indize dazu. Die gesamte Angabe ist dann folgende: [uvtw]
Gitterebenen: Auch hier kommt mit ein Indize hinzu. Die gesamte Angabe sieht hier wie folgt aus: (hkil)
Methode – Bestimmung der Indizes der Gitterrichtungen
Erneut legen wir einen Richtungsvektor durch den Koordinatenursprung und verlängern diesen mit zum Eckpunkt (Atom) einer Elementarzelle.
Anschließend lesen die in Gitterparameter angegebenen Projektionen des Vektors auf den Achsen a, b,d als Zahlen u,v,w abgelesen. Auf das Ablesen der Projektion auf der c-Achse verzichten wir.
Diese Zahlen genügen uns um jetzt die vier Ziffern [hkil] zu ermitteln:
oder
[NEU]
Die übrige Vorgehensweise mit gemeinsamen Teiler finden, usw. kennst du ja bereits.
Methode – Bestimmung der Indizes der Gitterebenen
Auch hier verwendest du die gleichen Gleichungen wir bei der Bestimmung der Indizes der Gitterrichtungen.
“Nachdem du jetzt einen Überblick zu den Gittereigenschaften erhalten hast, gehen wir im kommenden Kursabschnitt ausführlich auf die unterschiedlichen Formen von Gitterdefekten im Detail ein.”
Was gibt es noch bei uns?
Tausende interaktive Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Das erwartet dich!
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Auszüge aus unserem Kursangebot!
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++
Oder direkt >> Mitglied << werden und >> Zugriff auf alle 26 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++
Technikermathe.de meets Social-Media
Dein Technikermathe.de-Team