Mehr zu diesem Thema und der Werkstofftechnik findest du im Kurs: WT3-Werkstoffprüfung
Kristallsysteme – Grundlagen
Bevor wir nun mit der Einzelvorstellung der Kristallsysteme starten, folgt vorab ein Gesamtüberblick der Kristallsysteme.

Gittertypen
Ein Großteil der Metalle kristallisiert kubisch oder hexagonal.
Die Anzahl der Atome innerhalb einer Elementarzelle und deren Packungsdichte sind zwei Kenngrößen, die uns veranschaulichen, wie dicht die Atome räumlich angeordnet sind.
Mit n geben wir die Anzahl der Atome je Elementarzelle an. Dabei handelt es sich um die Eckatome und die in Flächen des einfachen geometrischen Grundkörpers eingelagerte Atome (flächenzentriert), sowie die mittig eingelagerten Atome (raumzentriert).
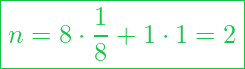
Die Eckatome und die flächenzentrierten Atome gehören auch zu den benachbarten Elementarzellen an. So kann ein Eckatom im Normallfall insgesamt 8 Elementarzellen zugeordnet werden.
Die Packungsdichte einer Elementarzelle hingegen berechnet sich aus dem Quotienten von Kugelvolumen innerhalb der Elementarzelle zu Gesamtvolumen der Elementarzelle.

Kristallsysteme – Kubische Gitter
„Ein kubisches System kennzeichnet, dass alle drei Achsen die gleiche Länge besitzen und im rechten Winkel zueinanderstehen.“
Das kubische Gitter hat die Erscheinung eines Würfels. Besonders Metalle haben diese Form.
Wir können drei Formen in Hinblick auf die Anordnung der Atome unterscheiden:
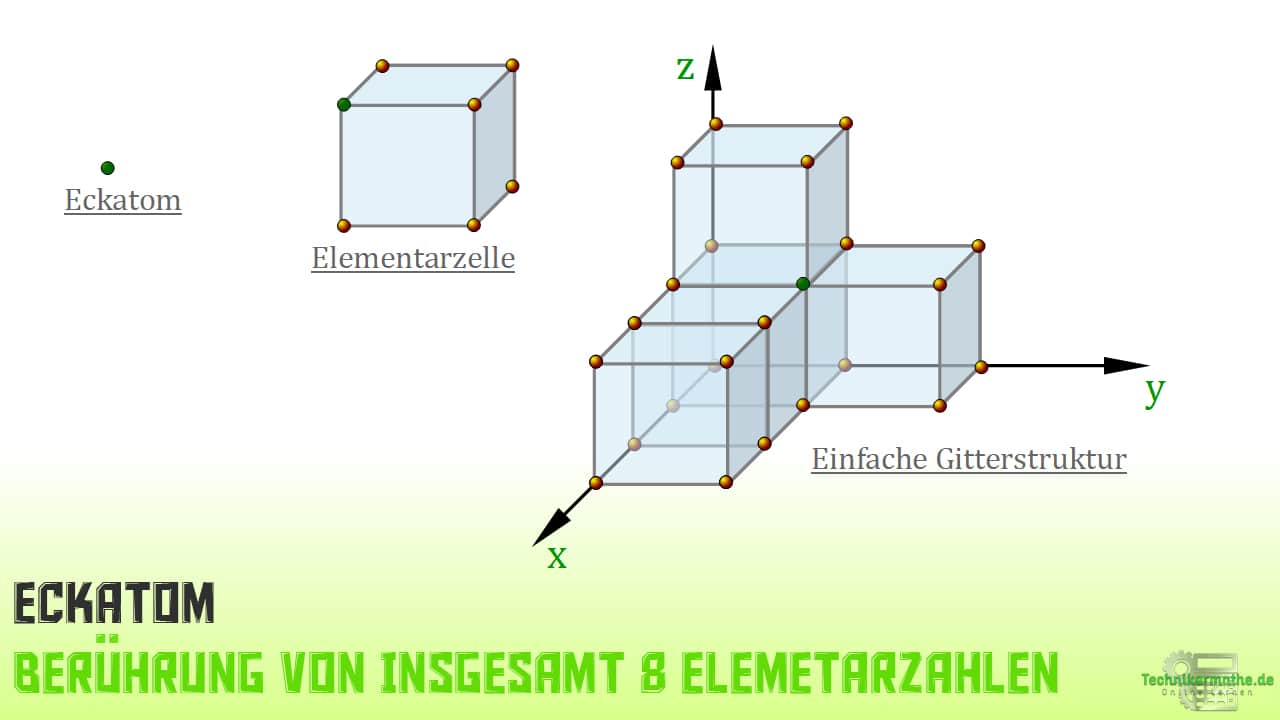
1 – Einfach kubisch oder kubisch primitiv (Kurzzeichen kp) mit 8 Atomen – (Englisch: sc = simple cubic)
2 – kubisch raumzentriert (Kurzzeichen krz) mit 9 Atomen – (Englisch: fcc = face centered cubic)
3 – kubisch flächenzentriert (Kurzzeichen kfz) mit 14 Atomen (Englisch: bcc = body centered cubic)
So sind die Gitterkonstanten: ![]()
Und die Achsenwinkel: ![]()
Einfach kubisches Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome, kommt jedoch selten bei reinen Metallen, sondern vielmehr bei Legierungen vor.

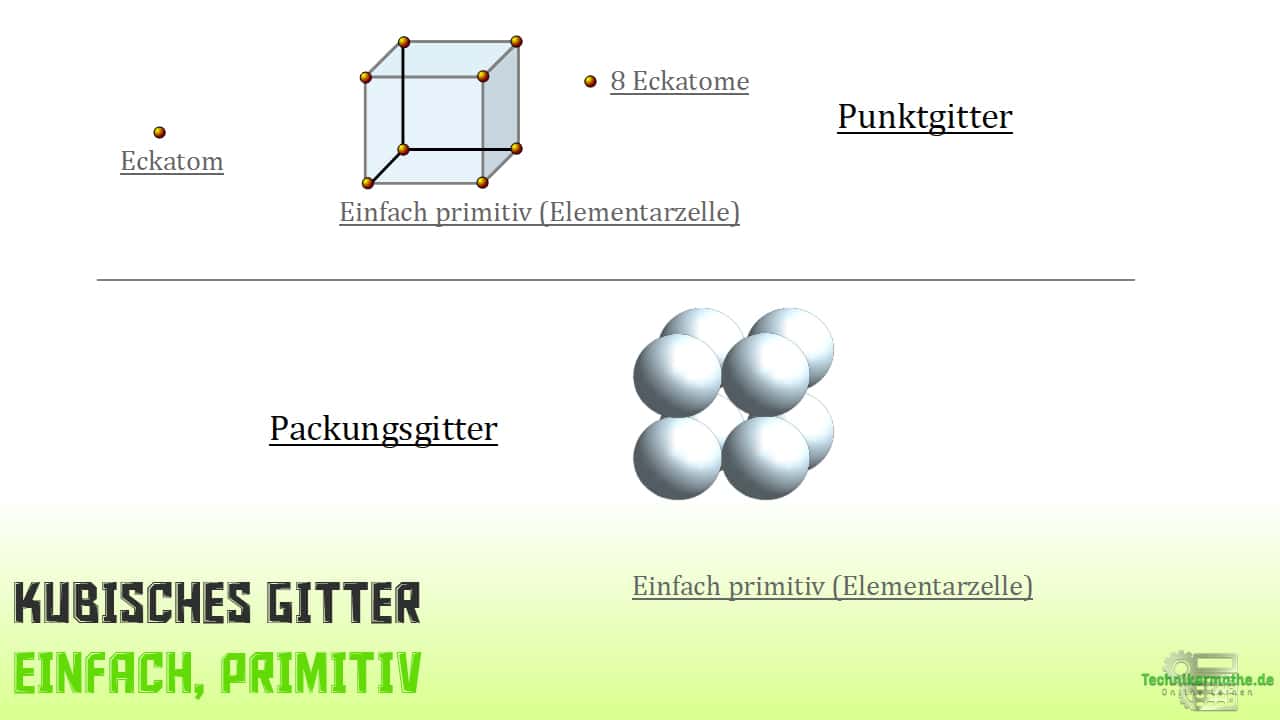
Kubisch-raumzentriertes Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome als Eckatome und zusätzlich ein mittig gelegenes Atom in der Elementarzelle. In Summe macht das 9 Atome.
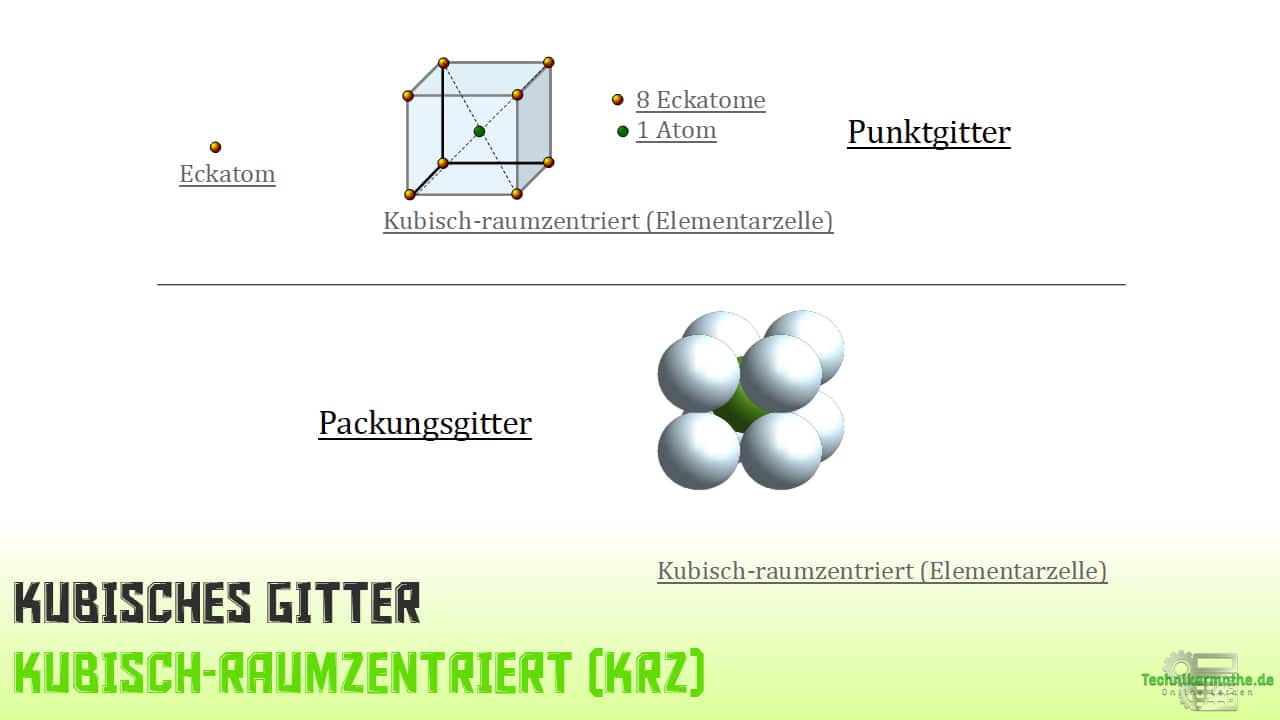
Kubisch-flächenzentriertes Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome als Eckatome und zusätzlich jeweils ein mittig gelegenes Atom in den Flächen der Elementarzelle. In Summe macht das 14 Atome.

Erscheinungen der krz- und kfz-Gitterstruktur – Beispiele
Zur Gruppe der Metalle mit einer krz-Gitterstruktur zählen
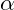 -Eisen (
-Eisen (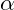 -Fe)
-Fe)- Chrom (Cr)
- Wolfram (W)
- Vanadium (V)
- Molybdän (Mo)
- Tantal (Ta)
Bei jedem Metall entsteht diese Struktur dadurch, dass sich ein einfach kubisches Gitter mit einem Eckatom in der Würfelmitte eines anderen einfach kubischen Gitters anlagert.
Zur Gruppe der Metalle mit einer kfz-Gitterstruktur zählen
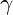 -Eisen (
-Eisen (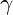 -Fe)
-Fe)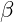 -Cobald (
-Cobald (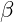 -Co)
-Co)- Aluminium (Al)
- Kupfer (Cu)
- Nickel (Ni)
- Gold (Au)
- Silber (Ag)
- Platin (Pt)
Bei jedem Metall entsteht diese Struktur dadurch, dass sich mehrere einfach kubische Gitter jeweils mit einem Eckatom in der Mitte der Seitenfläche eines anderen einfach kubischen Gitters anlagert.
Kristallsysteme – Tetragonale Gitter
„Ein tetragonales System kennzeichnet, dass die drei Achsen senkrecht zueinanderstehen, jedoch zwei in einer Ebene liegen und gleich lang sind. Die dritte Achse hingegen ist länger oder kürzer als die Hauptachse.“
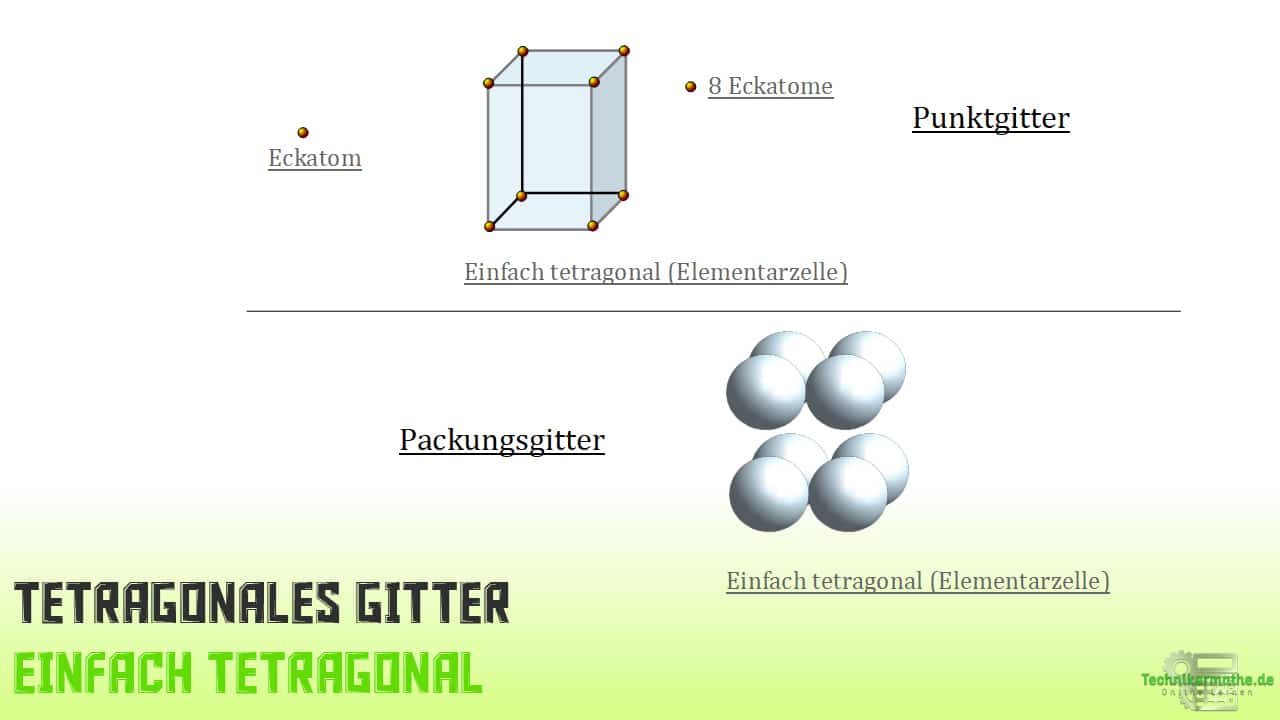
Das tetragonale Gitter hat die Erscheinung eines Würfels, der in eine Richtung gestreckt wurde. Besonders Mineralien haben diese Form.
Wir können zwei Formen in Hinblick auf die Anordnung der Atome unterscheiden:
1 – Einfach tetragonal oder tetragonal primitiv (Kurzzeichen tp) mit 8 Atomen
2 – kubisch raumzentriert (innenzentriert) (Kurzzeichen ti) mit 9 Atomen
Die Geometrie dieser beiden Ausprägungen ist identisch.
So sind die Gitterkonstanten: ![]()
Und die Achsenwinkel: ![]()
Einfach tetragonales Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome und kommt bei Mineralien vor.

Tetragonal raumzentriertes (innenzentriertes) Gitter

Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome als Eckatome und zusätzlich ein mittig gelegenes Atom in der Elementarzelle. In Summe macht das 9 Atome.
Erscheinungen der tP- und tI-Gitterstruktur – Beispiele
Zur Gruppe der Mineralien mit diesen Gitterstrukturen zählen
- Rubine
- Saphire
- Islandspat
- Ankerit
Neben der Form eines Prismas, zählt man auch Trapezoeder sowie Einfachpyramiden und Doppelpyramiden hinzu. Denn auch diese besitzen zwei gleichlange Seite in der Ebene sowie eine verkürzte oder verlängerte Seite, die senkrecht auf der Ebene steht.
Kristallsysteme – Orthorhombische Gitter
„Ein Orthorhombisches (rhombisches) System kennzeichnet, dass drei unterschiedlich lange Achsen im rechten Winkel zueinanderstehen.“

Das rhombische Gitter hat die Erscheinung eines Ziegelsteins, der in eine Richtung gestreckt wurde. Besonders Mineralien haben diese Form.
Wir können vier Formen in Hinblick auf die Anordnung der Atome unterscheiden:
1 – Einfach rhombisch oder rhombisch primitiv (Kurzzeichen oP) mit 8 Atomen
2 – Rhombisch basiszentriert (Kurzzeichen oB) mit 10 Atomen
3 – Rhombisch flächenzentriert (Kurzzeichen oF) mit 14 Atomen
2 – Rhombisch raumzentriert (innenzentriert) (Kurzzeichen oI) mit 9 Atomen
Die Geometrie dieser beiden Ausprägungen ist identisch.
So sind die Gitterkonstanten: ![]()
Und die Achsenwinkel: ![]()
Einfach rhombisches Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome und kommt bei Mineralien vor.

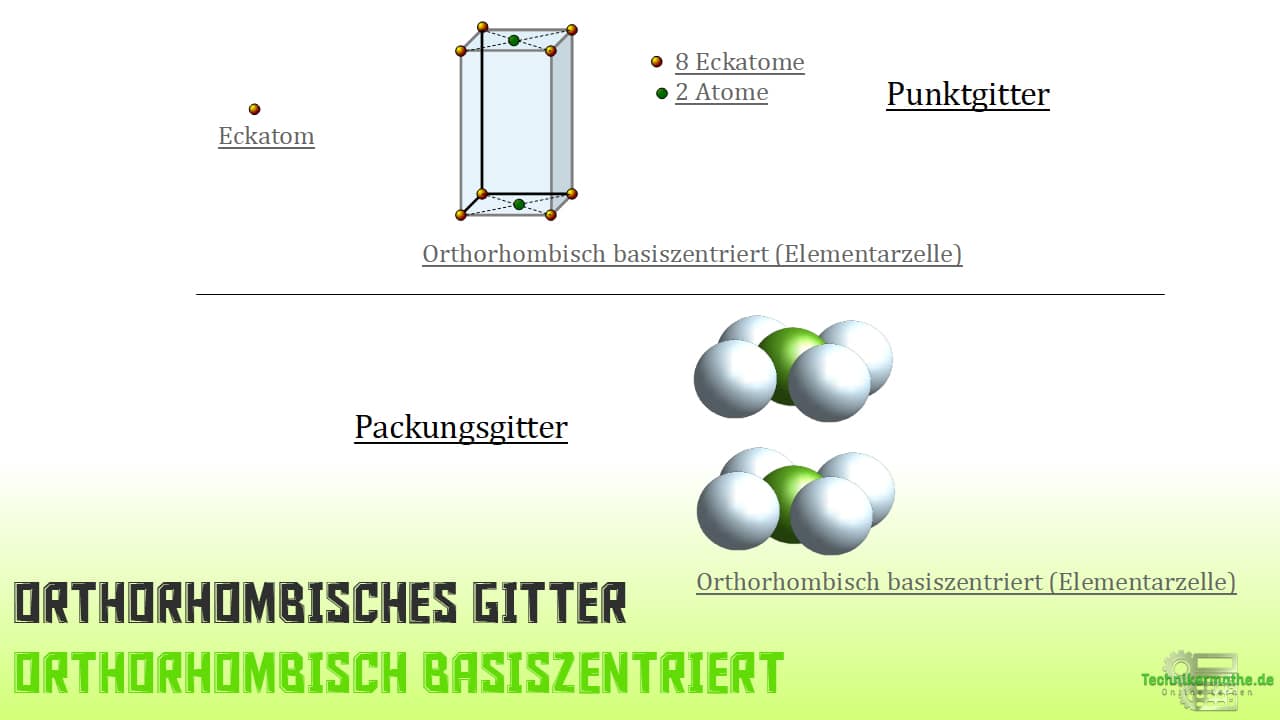
Rhombisch basiszentriertes Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome als Eckatome und zusätzlich zwei mittig gelegene Atome auf den Flächen der Ober- und Unterseite der Elementarzelle. In Summe macht das 10 Atome.
Rhombisch flächenzentriertes Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome als Eckatome und zusätzlich sechs mittig gelegene Atome auf allen Seitenflächen der Elementarzelle. In Summe macht das 14 Atome.
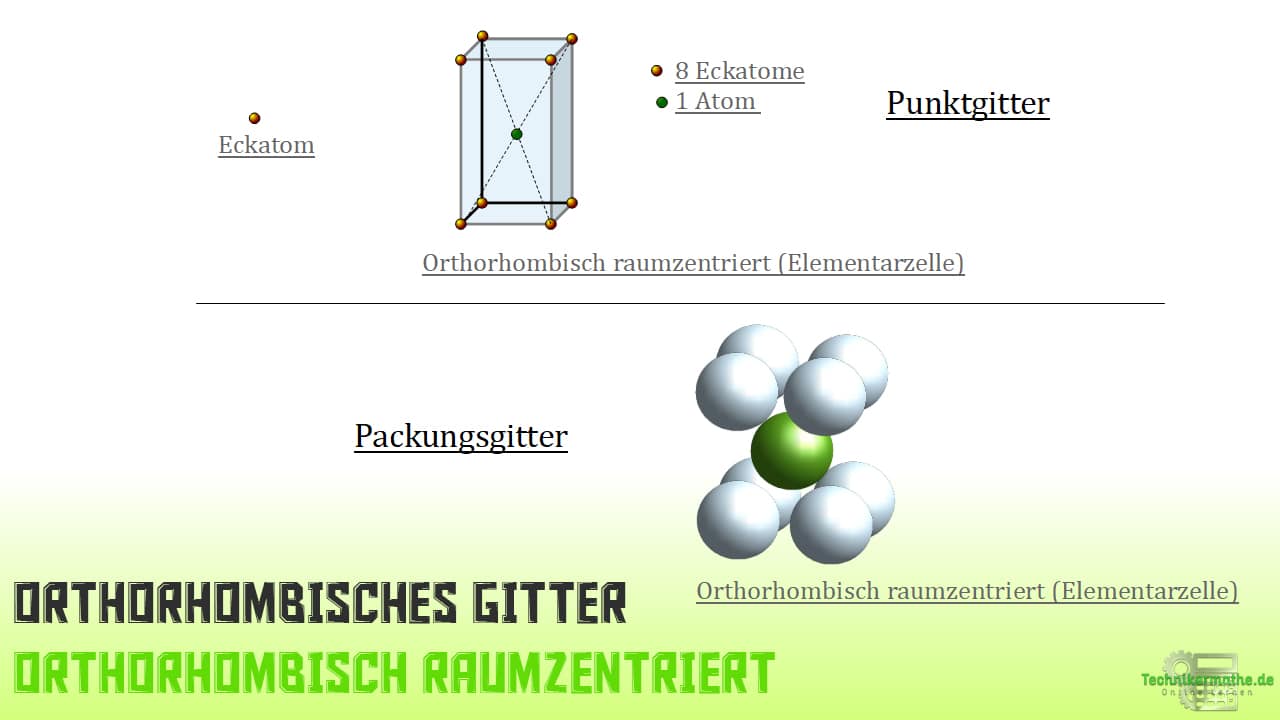
Rhombisch raumzentriertes (innenzentriertes) Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome als Eckatome und zusätzlich ein mittig gelegenes Atom in der Elementarzelle. In Summe macht das 9 Atome.
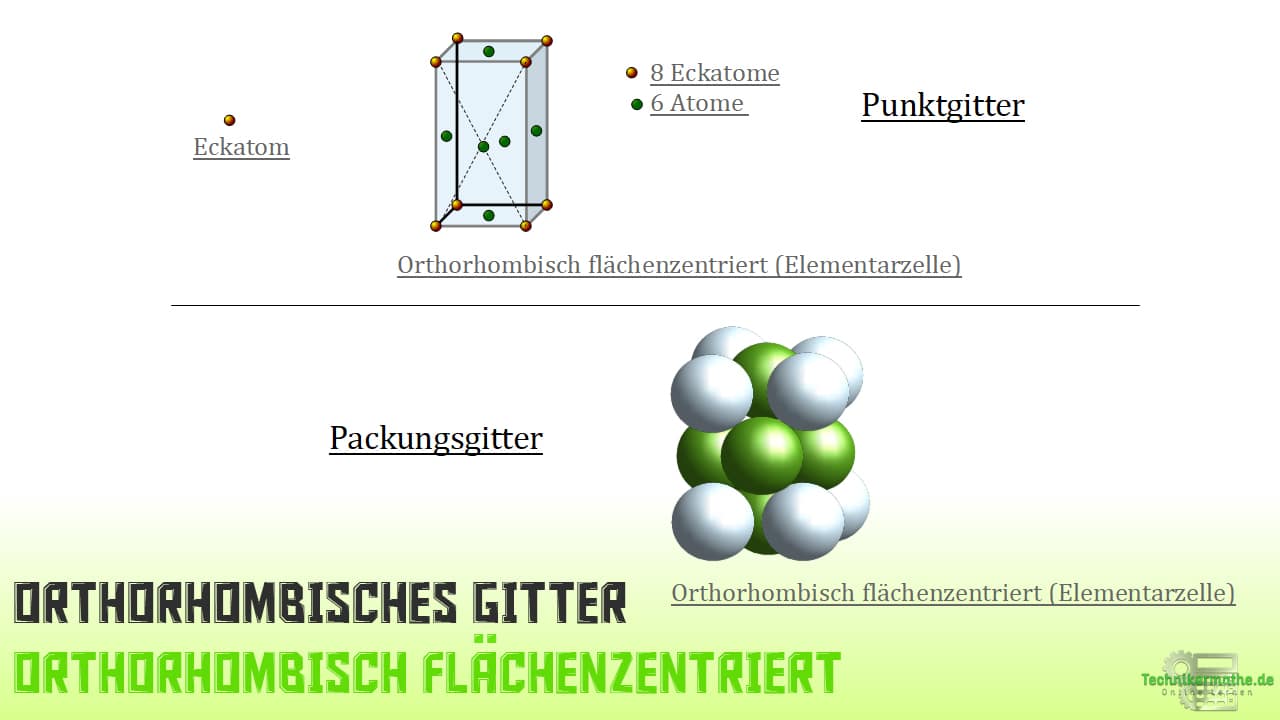
Erscheinungen der oP-, oB, oF und oI-Gitterstruktur – Beispiele
Zur Gruppe der Mineralien mit diesen Gitterstrukturen zählen
- Aragonit
- Prehnit
- Andalusit
- Purpurit
Neben der Form eines Prismas, zählt man auch Einfachpyramiden und Doppelpyramiden hinzu.
Kristallsysteme – Monokline Gitter
„Ein monoklines System kennzeichnet, dass von den drei unterschiedlich langen Achsen zwei senkrecht zueinanderstehen. Die dritte Achse hingegen verläuft schief dazu.“
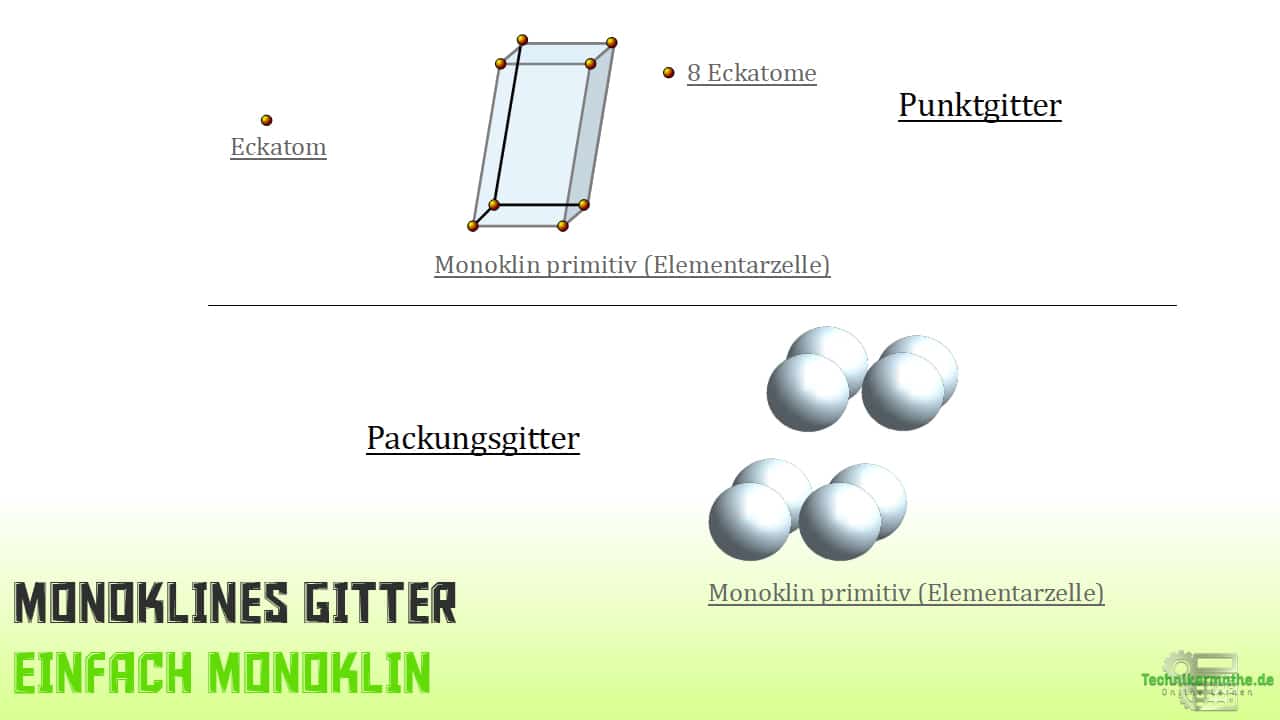
Das monokline Gitter hat die Erscheinung eines schiefen (in eine Richtung) Ziegelsteins, der in eine Richtung gestreckt wurde. Bereits das Wort monoklin (einzeln…) , deutet daraufhin, dass hier ein Winkel vorliegt, welcher von den 90° der anderen Winkel abweicht.
Auch hier handelt es sich um Mineralien. Es handelt sich um eine Abwandlung des rhombischen Gitters. Es kommt zu einer Verzerrung der zur c-Achse senkrechten, rechteckigen Fläche statt.
Wir können zwei Formen in Hinblick auf die Anordnung der Atome unterscheiden:
1 – Einfach monoklin oder monoklin primitiv (Kurzzeichen mP) mit 8 Atomen
2 – Monoklin basiszentriert (Kurzzeichen mB) mit 10 Atomen
Die Geometrie dieser beiden Ausprägungen ist identisch.
So sind die Gitterkonstanten: ![]()
Und die Achsenwinkel: ![]() und
und ![]()
Es kommt zu einer Änderung des Winkels ![]() .
.
Einfach monoklines Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome und kommt bei Mineralien vor.
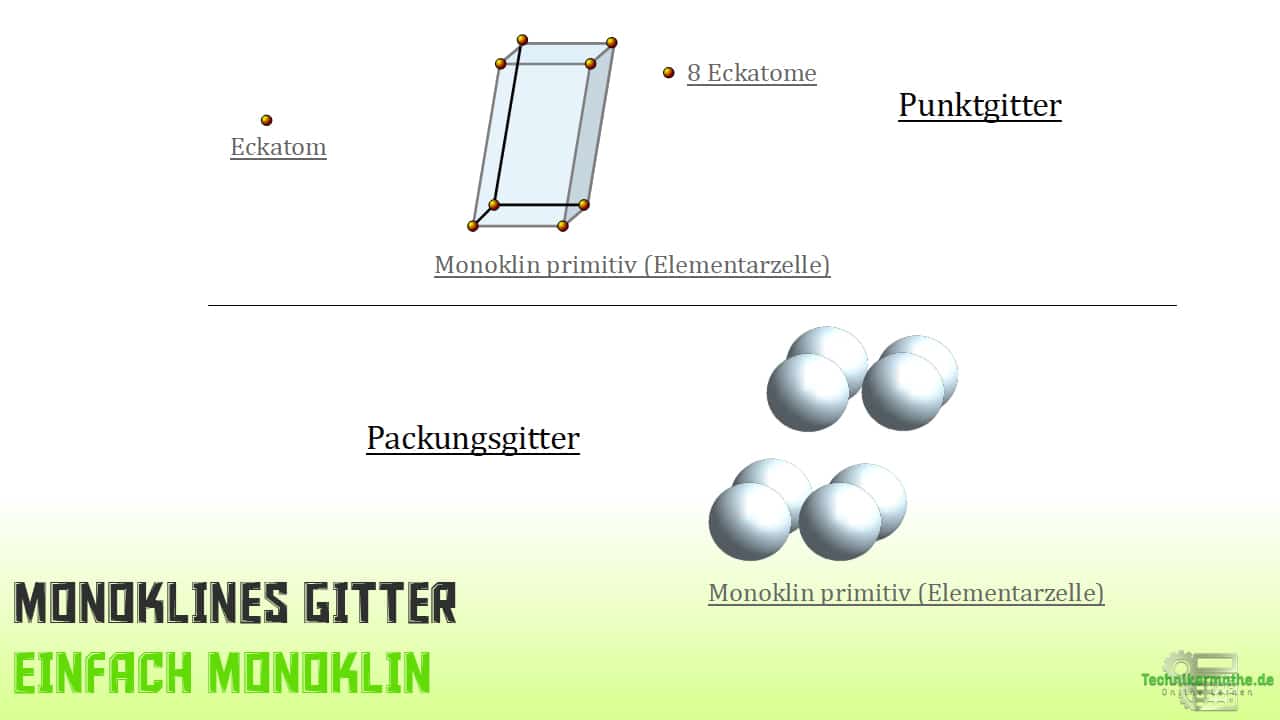
Monoklin basiszentriertes Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome als Eckatome und zusätzlich zwei mittig gelegene Atome auf den Flächen der Ober- und Unterseite der Elementarzelle. In Summe macht das 10 Atome.

Erscheinungen der mP- und mB-Gitterstruktur – Beispiele
Zur Gruppe der Mineralien mit diesen Gitterstrukturen zählen
- Schwefel (S)
- Diopsid
- Azurit
- Krokoit
Neben der Form eines Prismas, zählt man Doppelpyramiden hinzu.
Kristallsysteme – Trikline Gitter
„Ein triklines System kennzeichnet, dass alle drei Achsen unterschiedlich in Bezug auf Länge und gegenseitiger Neigung zueinander sind.
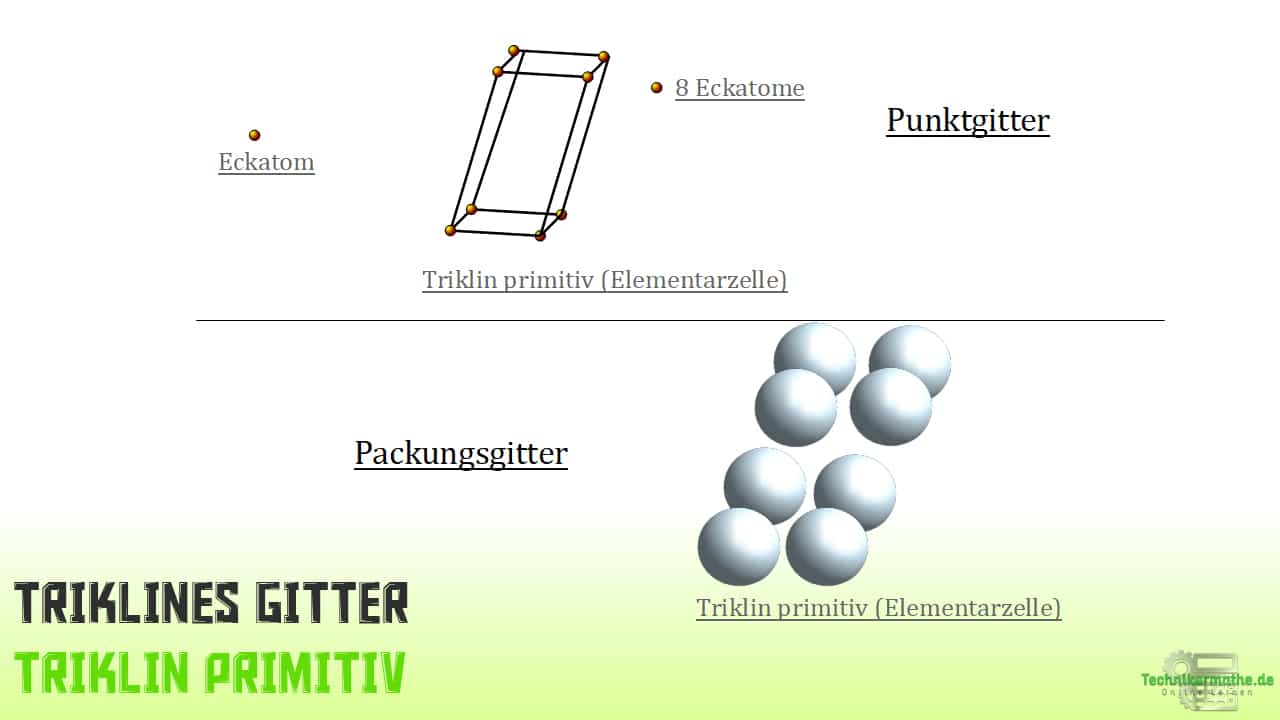
Bereits das Wort triklin (dreifach…) , deutet daraufhin, dass hier drei Winkel vorliegen, welche alle von den 90° abweichen. Das Gitter hat die Erscheinung eines allseitig schiefen Ziegelsteins.
Auch hier handelt es sich um Mineralien. Es handelt sich um eine Abwandlung des rhombischen Gitters. Es kommt zu einer Verzerrung der zur c-Achse senkrechten, rechteckigen Fläche statt.
Wir können eine Form in Hinblick auf die Anordnung der Atome festlegen:
1 – Einfach triklin oder triklin primitiv (Kurzzeichen tP) mit 8 Atomen
So sind die Gitterkonstanten: ![]()
Und die Achsenwinkel: ![]()
Es kommt zu einer Änderung aller Winkel.
Einfach triklines Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 8 Atome und kommt bei Mineralien vor.

Erscheinungen der tP-Gitterstruktur – Beispiele
Zur Gruppe der Mineralien mit dieser Gitterstruktur zählen
- Okenit
- Rhodonit
- Türkis
- Kyanit
Bei diese Gitterform lassen sich Flächenpaare bilden.
Kristallsysteme – Hexagonale Gitter
„Ein hexagonales System kennzeichnet, dass es auch vier anstatt drei Achsen besteht. Dabei liegen drei Achsen in einer Ebene und sind gleich lang. Dabei schneiden sie sich um Winkel von 120°. Die vierte ungleichwertige Achse steht senkrecht zu diesen.

Die Erscheinung ist, die eines Sechskantmaterials, welches gerade abgeschnitten wurde.
Das Hexagonale Gitter unterscheidet sich stark von den anderen Gitterstrukturen, denn hier sind die Basisflächen sechseckig und die Anzahl der Gesamtflächen ist 8. Es handelt sich um eine Struktur, die vorrangig bei Metallen mit Legierungselementen auftritt. In Reinmetallen tritt diese Form nicht auf.
Es besteht also aus mindestens zwei gleichartigen Atomen.
Wir können eine Form in Hinblick auf die Anordnung der Atome festlegen:
1 – Einfach hexagonal oder hexagonal primitiv (Kurzzeichen hP) mit 14 Atomen (Englisch: hcp = hexagonal closed packed)
So sind die Gitterkonstanten: ![]()
Und die Achsenwinkel: ![]() und
und ![]()
Einfach hexagonale Gitter
Wie du bereits weißt, hat diese Erscheinung der Elementarzelle 12 Atome und kommt bei Metallen vor.

Im Raumgitter selber können sich drei Atome befinden:

Es handelt sich hierbei um die dichteste Gitterart, denn es können zwei hexagonal primitive Gitter ineinander liegen. Das wiederum führt dazu, dass der leere Raum zwischen den Atomen minimal wird.
Erscheinungen der tP-Gitterstruktur – Beispiele
Zur Gruppe der Metalle mit Legierungselementen mit dieser Gitterstruktur zählen
- Cadmium
- Magnesium
- Zink
- Titan
Diese legierten Metalle haben ein nur sehr geringes Umformungsvermögen.
Das dichteste hexagonale primitive Gitter hat mit einem Wert von 0,74 die gleiche Packungsdichte wie das kubisch flächenzentrierte Gitter. Diese Gleichheit ist aber nur gegeben, wenn im kubisch flächenzentrierten Gitter auch dichtest gepackte hexagonale Gitterebenen existieren.
Kristallsysteme – Rhomboedrische (trigonale) Gitter
„Ein rhomboedrisches (trigonales) System kennzeichnet, dass auch hier drei von vier Achsen in einer Ebene liegen und sich im Winkel von 120° schneiden. Die vierte Achse steht wieder senkrecht zu diesen.
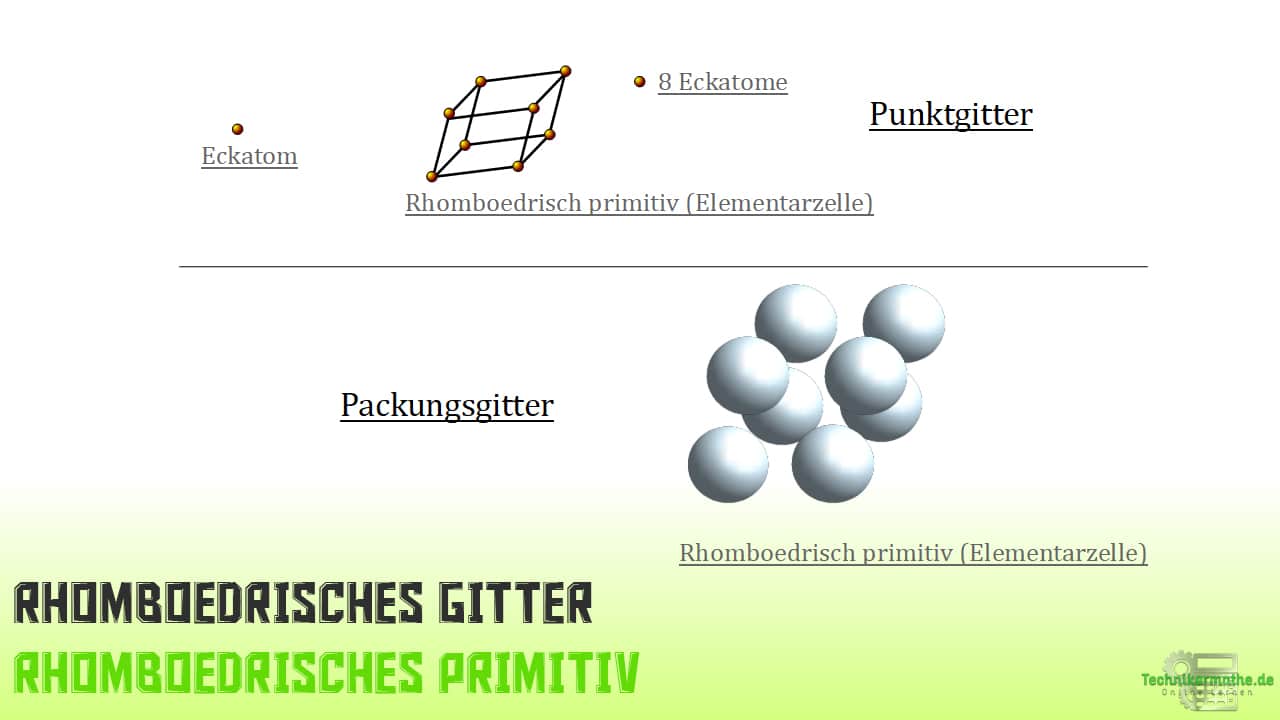
Das rhomboedrische System hat die Erscheinung eines allseitig schiefen Würfels.
Wir können eine Form in Hinblick auf die Anordnung der Atome festlegen:
1 – Einfach rhomboedrisch oder rhomboedrisch primitiv (Kurzzeichen rP) mit 8 Atomen
So sind die Gitterkonstanten: ![]()
Und die Achsenwinkel: ![]()
Das Rhomboedrische und hexagonale System fasst man häufig als hexagonales System zusammen.
Der Unterschied der beiden Systeme liegt darin, dass bei hexagonalen Systemen die betrachtete Grundfläche sechseckig ist und bei dem Rhomboedrischen System ist die Grundfläche hingegen dreieckig (trigonal).
Kristallsysteme – Bravais-Gitter
In Summe haben wir nun 14 verschiedene Gitterarten, die sich 7 unterschiedlichen Kristallsystemen zuordnen lassen. Man kennt diese Zusammenfassung unter dem Begriff Bravais-Gitter.
Unterscheidungsmerkmale
Als Unterscheidungsmerkmal wählte Pearson, die Geometrie einer Gitterart. Denn ein Kristall setzt sich immer aus einem Gitter und einer zugehörigen Basis zusammen. Man spricht dann von einem Kristallgitter oder einer Kristallstruktur.
Gitter: Regelmäßige Anordnung von Atomen im dreidimensionalen Raum.
Basis: Sich wiederholende Struktur innerhalb eines Gitters.
So ist es Pearson gelungen mit Hilfe der drei Gitterkonstanten (a,b,c) und den drei Gitterwinkeln (![]() ) die Gitterarten eindeutig zu charakterisieren.
) die Gitterarten eindeutig zu charakterisieren.
Unter zur Hilfenahme von zusätzlichen Symmetrieoperationen erhöht sich die Anzahl der Gitterarten auf 14.
Kristallsysteme – Symmetrieoperationen
Wir können vier Symmetrieoperationen unterscheiden mit deinen sich die Kristallgitter voneinander unterscheiden lassen.
- Translation: Erfolgt um einen beliebigen Gittervektor
- Spiegelung: Erfolgt an den Ebenen
- Inversion: Bezieht sich auf einen Gitterpunkt
- Rotation: Erfolgt um einen Gittervektor herum.
Nachdem du jetzt einen Überblick zu den Kristallsystemen erhalten hast, gehen wir im kommenden Kursabschnitt ausführlich auf die Gittereigenschaften im Detail ein.
Was gibt es noch bei uns?
Tausende interaktive Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Das erwartet dich!
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Auszüge aus unserem Kursangebot!
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++
Oder direkt >> Mitglied << werden und >> Zugriff auf alle 26 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 7,40 EUR/Monat
++ Besser geht’s nicht!! ++
Technikermathe.de meets Social-Media
Dein Technikermathe.de-Team
Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++
Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++
Technikermathe.de meets Social-Media
Dein Technikermathe.de-Team









