In diesem ersten Kursabschnitt verschaffen wir dir einen Überblick zum Aufbau von kristallinen Werkstoffen und gehen dabei auf die Gitterstrukturen von Werkstoffen ein. Denn Gitterstrukturen verschaffen die einen genauen Überblick über den Aufbau und die Eigenschaften eines Werkstoffes

Gitterstrukturen – Metallgitter & Atomgitter
Die Bausteine von Metallen in fester Form sind Atome.
Die Antwort auf die Frage, weshalb Metalle eine feste Struktur aufweist, liefert das Elektronengasmodell.
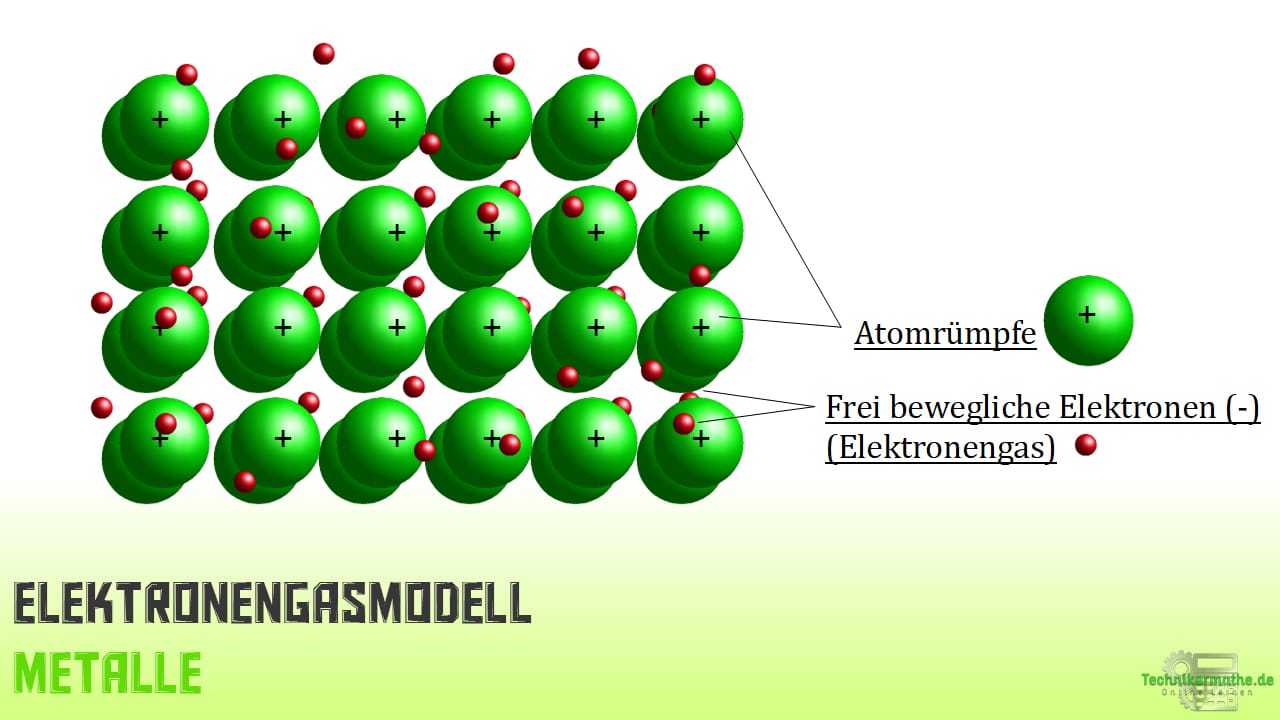
So liegen die Metallatome in einer geordneten Gitterstruktur vor. Umgeben sind die Metallatome von einen Elektronengas, welches sich aus abgegebenen Valenzelektronen zusammensetzt.
Diese Valenzelektronen sind frei beweglich und halten durch elektrostatische Anziehung, die durch die Abgabe der Elektronen positiv geladenen Atomrümpfe zusammen.
Innerhalb der Festkörper finden sich Gitterstrukturen von Metallatome, die regelmäßig in Schichten angeordnet sind.
Wenn es sich um ein reines Metall, also ein Metall ohne zusätzliche Legierungselemente, handelt, sind alle Atome gleich groß und können sehr eng aneinander gepackt werden.
Gitterstrukturen – Koordinationszahl
Vielleicht hast du schon mal von der „dichtesten Kugelpackung“ gehört, dies ist eine typische Struktur von Metallen, bei welcher Jedes Metallatom vom zwölf weiteren Metallatomen umgeben ist.
Sechs Metallatome befinden sich auf der gleichen Ebene und drei in der Ebene darüber sowie drei in der Ebene darunter.
Das 12 Metallatome unser betrachtetes Metallatom umgeben, können wir ganz einfach mit Hilfe der Koordinationszahl ausdrücken, diese hat bei diesem Strukturtyp die Angabe 12.
Die gute Verformbarkeit von Metallen ist auch auf die Struktur zurückzuführen. Denn die einzelnen Metallatomschichten lassen sich gut gegeneinander verschieben, da sie ja insgesamt durch das Elektronengas zusammengehalten werden.
Dieser Vorgang könnte dich an eine Handvoll magnetischer Kugel erinnern, denn diese lassen sich ja auch in ihrer Gesamtform verändern, aber der Zusammenhalt (hier aufgrund des Magnetismus) bleibt bestehen.
Werden dem Metall Fremdatome innerhalb des Metallgitter durch Legierungselemente hinzugefügt, so nimmt die Verschiebbarkeit innerhalb des Metallgitter ab.
Aus diesem Grund sind einige Legierungen, als Metall plus Legierungselemente, härter und spröder als das reine Grundmetall.
Diesen Effekt kann man besonders gut bei Bronze nachweisen. Denn Bronze ist härter als deren Bestandteile Zinn und Kupfer in Reinform.
Gitterstrukturen – Kristalliner Zustand
Je nachdem welche Kräfte wirken, stellt sich ein bestimmter Atomabstand (Bindungslänge) ein.
Die Kristallstruktur ist auch äußerlich mit bloßem Auge durch seine regelmäßigen Flächen und symmetrischen Anordnungen erkennbar.
Auf der anderen Seite haben wir aber auch Flüssigkeiten und falsche Festkörper wie einige Kunststoffe, die amorph, also gestaltlos daher kommen. Ihre Atome haben keine Ordnung in ihrer Struktur, weshalb sie sich stark von Kristallstrukturen unterscheiden.
- kristallin = geordnete (Struktur)
- Amorph = ungeordnete, gestaltlose (Struktur)
Aus der Sicht eines Technikers, lässt sich auch zwischen einer Fernordnung und einer Nahordnung unterscheiden.
Fernordnung = Kristallstruktur: Bausteine sind in Gittern geordnet mit einer endlosen Dimension.
Nahordnung = Flüssigkeiten: Bausteine sind höchstens in kleinen Bereichen geordnet.
Gitterstrukturen – Raumgitter
Das Raumgitter und die Dimensionen eines Kristalls lassen sich mit Hilfe vom Röntgenfeinstrukturanalysen bestimmen.
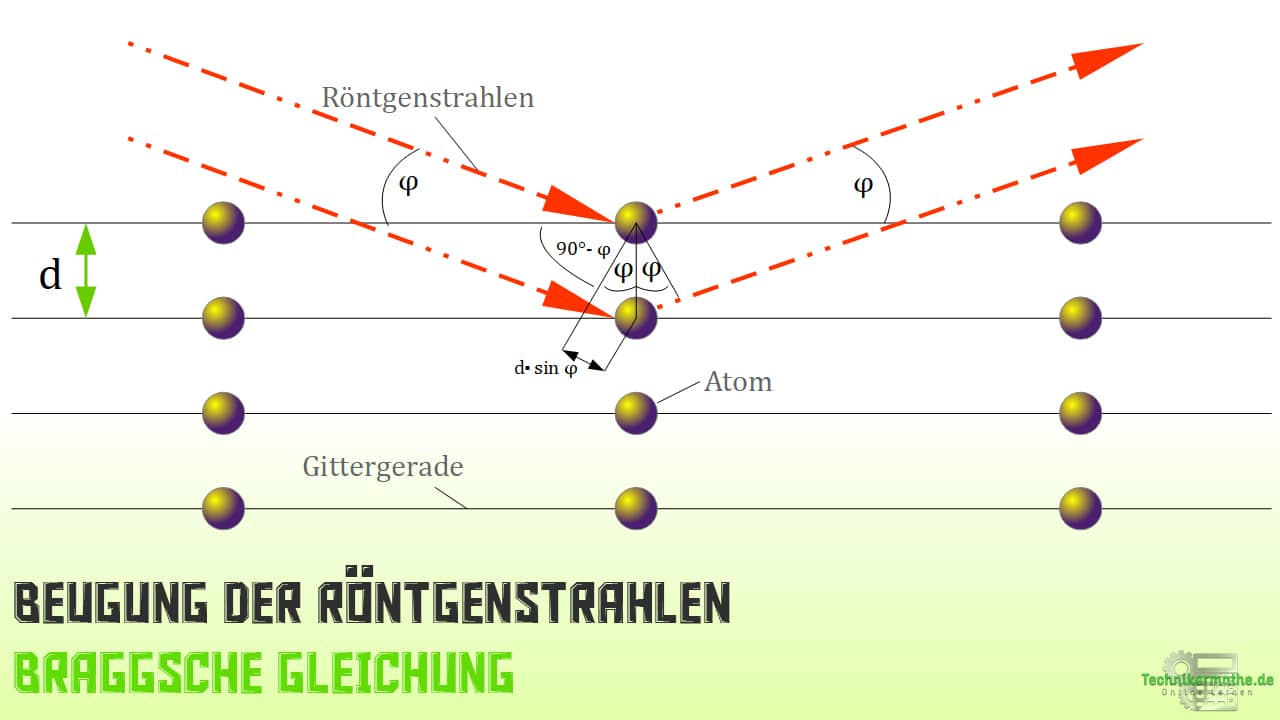
Hier nutzt man Röntgenstrahlen. Mit diesen werden die Kristalle bestrahlt und es kommt zu Interferenzerscheinungen, weil die Wellenlängen der Röntgenstrahlen in der Größenordnung der Atomabstände liegen.
Für die Berechnung der Messergebnisse verwendet man dann die Braggsche Gleichung.
![]()
Kennzahlen
![]() Netzebenenabstand
Netzebenenabstand
![]() Glanzwinkel
Glanzwinkel
![]() Beugungsordnung
Beugungsordnung
![]() Wellenlänge
Wellenlänge
Gitterstrukturen – Beschreibung des Raumgitters
Das Raumgitter besitzt einige geometrische Größen, die wir dir nachfolgend aufführen möchten.
Gittergerade
„Es handelt sich um die eindimensionale Betrachtung des Raumgitters.“
Als Gittergerade beschreibt man die Gerade auf der sich in regelmäßigen Abständen Atome befinden:
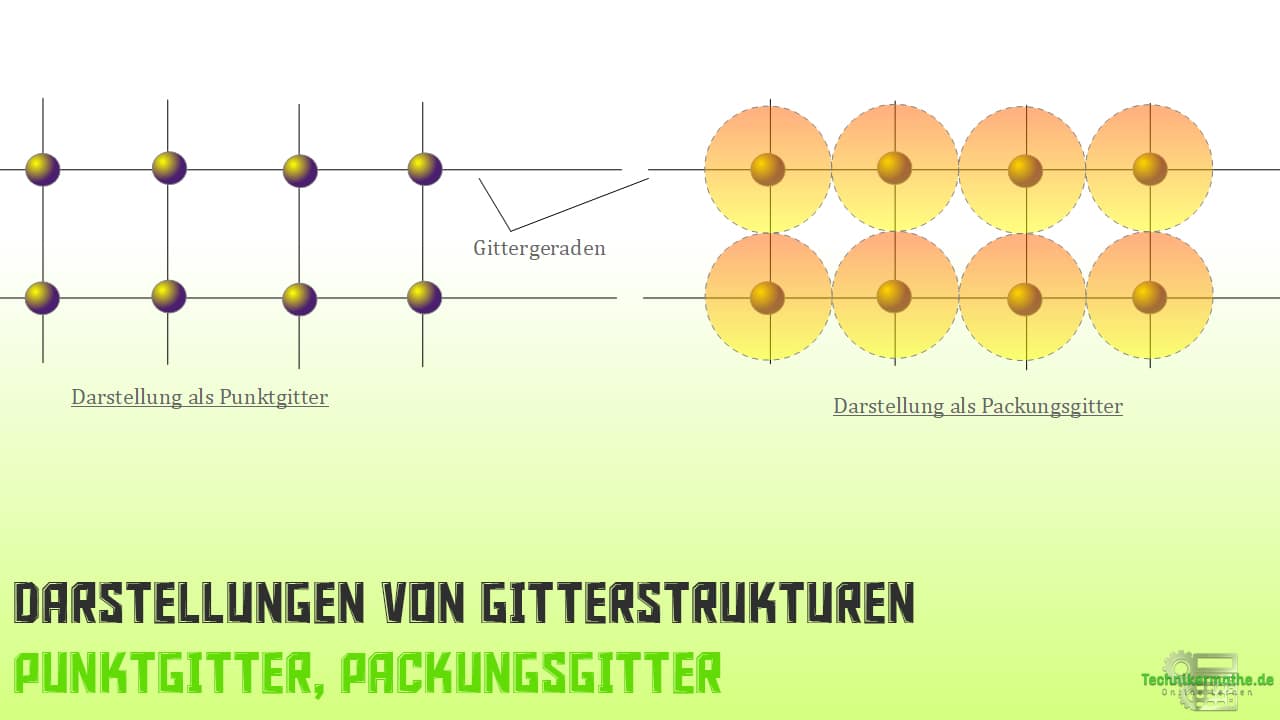
Wie du der Abbildung entnehmen kannst, erfolgt die Darstellung entweder als Packungsgitter oder als Punktgitter.
Gitterebene
„Es handelt sich um die zweidimensionale Betrachtung des Raumgitters.“
Die Gitterebene, in der Literatur auch Netzebene genannt, ist eine Ebene, die regelmäßig mit Atomen besetzt ist.
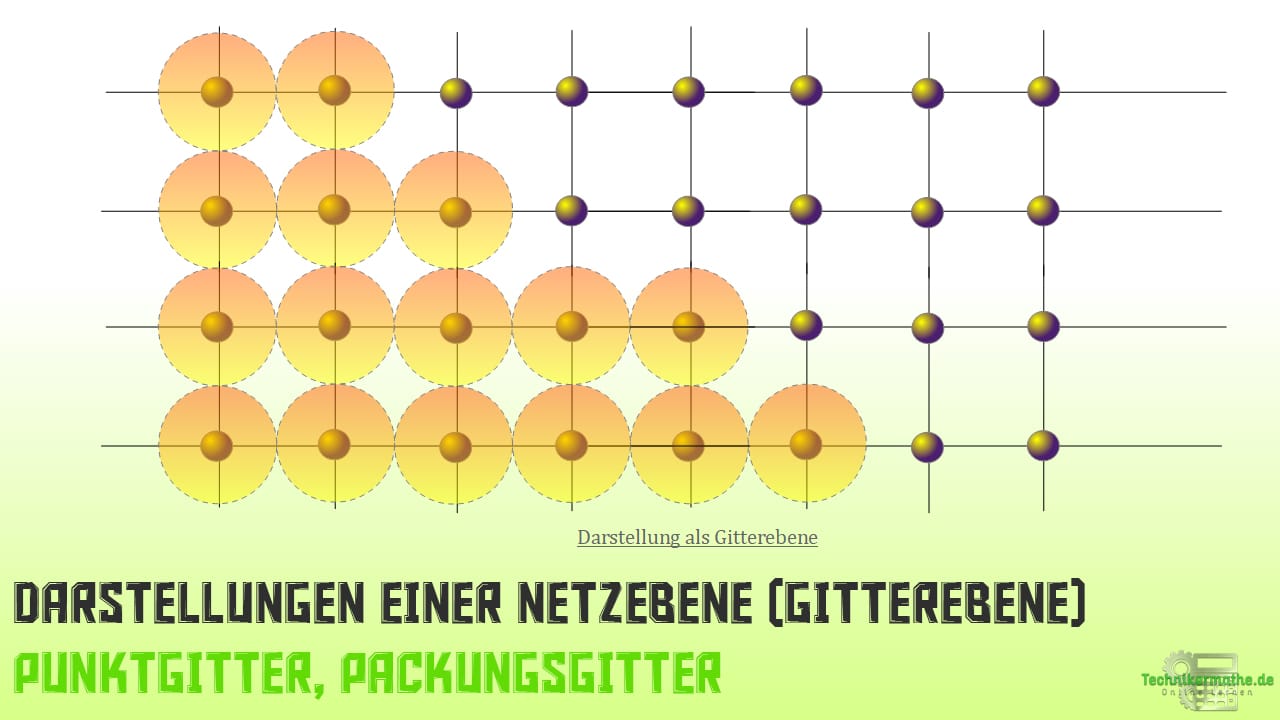
Auch hier unterscheiden wir die Darstellung als Packungsgitter und als Punktgitter.
Raumgitter
„Es handelt sich um die dreidimensionale Betrachtung des Raumgitters.“
Das Raumgitter ermöglicht eine komplette Betrachtung der Atomanordnung und gibt uns die finale Auskunft darüber, welche Art von Kristall uns vorliegt.
Elementarzelle
„Es handelt sich um die kleine Volumeneinheit des Raumgitters“
Die Elementarzelle hat einen besonderen Vorteil, denn sie weist alle Symmetriemerkmale eines Kristallsystems auf. Alle anderen drumherum befindlichen Elementarzellen besitzen die gleichen Merkmale, weshalb wir ausgehend von der einen Zelle auf den ganzen Kristall Rückschlüsse ziehen können.
Elementarzelle
Erneut greifen wir die Beschreibung der Elementarzelle aus dem Vorherigen Abschnitt auf.
Wiederholung
„Es handelt sich um die kleine Volumeneinheit des Raumgitters“
Die Elementarzelle hat einen besonderen Vorteil, denn sie weist alle Symmetriemerkmale eines Kristallsystems auf. Alle anderen drumherum befindlichen Elementarzellen besitzen die gleichen Merkmale, weshalb wir ausgehend von der einen Zelle auf den ganzen Kristall Rückschlüsse ziehen können.
Somit dient die Elementarzelle der genauen Beschreibung eines Gitters.
Gitterkonstanten
Für eine eindeutige Beschreibung legen wir mit den Achsabschnitten a,b,c Gitterkonstanten bzw. Gitterparameter auf den Koordinatenachsen x,y,z fest.
Diese sind das erste von insgesamt zwei Beschreibungsmerkmalen.

In den meisten Fällen liegen die Größen bei 0,25 nm bis hin zu 0,50 nm.
![]()
Um dir mal einen guten Eindruck von den Dimensionen zu geben mit denen wir hier arbeiten, kannst du dir merken, dass auf der Länge von einem Millimeter Kristall zwischen 2-4 Millionen Atome liegen.
Achsenwinkel
Die Achsenwinkel sind das zweite Beschreibungsmerkmal der Elementarzelle.
Wir unterscheiden ausgehend vom Ursprung des Koordinatensystems die Winkel ![]() .
.
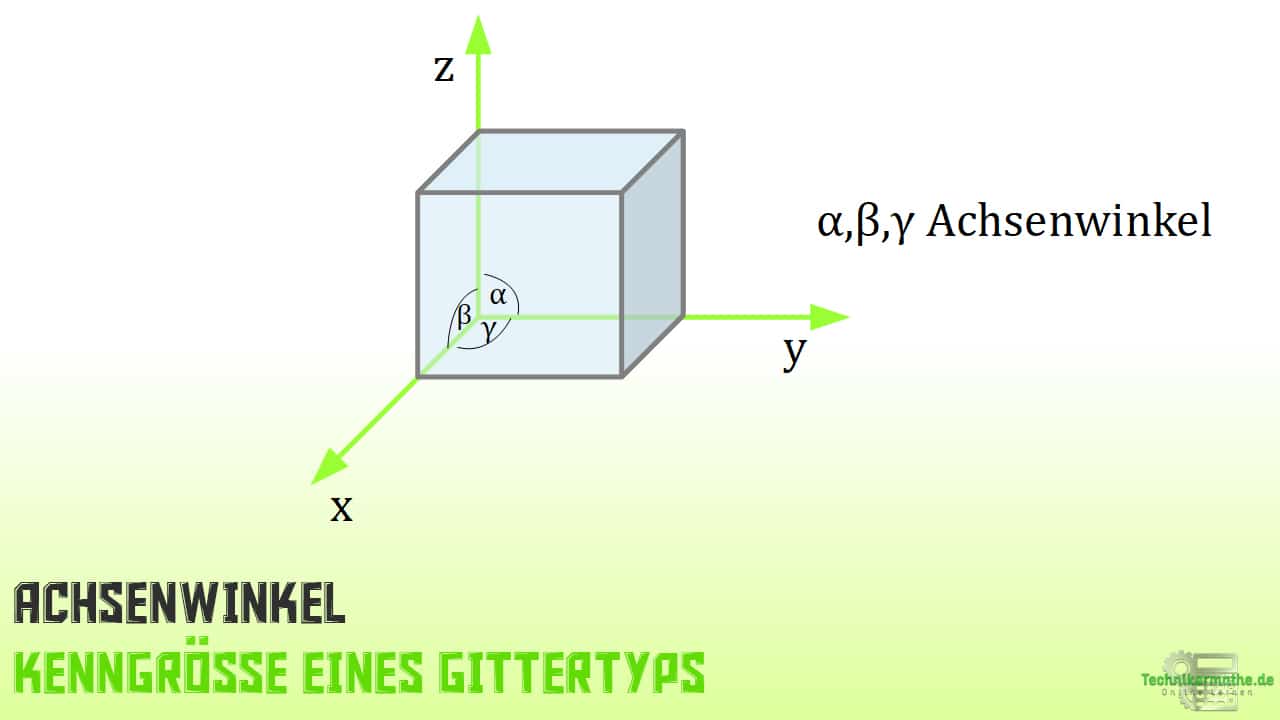
Die Winkel können 90° entsprechen, aber auch davon abweichen.
Was gibt es noch bei uns?
Was ist Technikermathe.de?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Interaktive Übungsaufgaben

Quizfrage 1
Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?
Auszüge aus unserem Kursangebot
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++
Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++
Technikermathe.de meets Social-Media
Dein Technikermathe.de-Team








