PH5 – Volumenänderungsarbeit (Nutzarbeit, Verschiebearbeit) – [Erklärung, Beispiele, Berechnung, Videos]

Ein Teil der Arbeit W, die einem geschlossenen System zugeführt bzw. vom System abgegeben werden kann, ist die Volumenänderungsarbeit.

Volumenänderungsarbeit W_V wird verrichtet, wenn auf ein abgeschlossenes Gas eine Kraft F über einen Weg s wirkt und sich dabei das Volumen ΔV des Gases ändert.

In dieser Lerneinheit betrachten wir die Volumenänderungsarbeit mit und ohne Umgebungsdruck und unterscheiden die Nutzarbeit und Verschiebearbeit.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH5 – Wärmelehre auf Technikermathe.de

Für ein optimales Verständnis helfen dir zwei anschauliches Rechenbeispiele zu dem Thema.

Volumenänderungsarbeit – Definition

Die Volumenänderungsarbeit, oft auch als Volumenarbeit bezeichnet, ist eine physikalische Größe, die in der Thermodynamik und in der Mechanik verwendet wird, um die Arbeit zu beschreiben, die bei einer Volumenänderung eines Systems geleistet wird. Diese Arbeit kann bei verschiedenen Prozessen auftreten, wie beispielsweise der Expansion oder Kompression eines Gases.

Volumenänderungsarbeit – Beispiele im Alltag

Luftkompressor: Wenn du beispielsweise deine Autoreifen aufpumpst, wird Arbeit verrichtet, um die Luft in den Reifen zu komprimieren. Diese Arbeit wird in Form von Volumenänderungsarbeit geleistet.
Atemarbeit: Bei jedem Atemzug wird Arbeit verrichtet, um deine Lunge zu dehnen und zu komprimieren. Die Muskeln in deiner Brust und deinem Zwerchfell leisten Volumenänderungsarbeit, um die Lungenkapazität zu ändern.
Hydraulikheber: Hydraulische Heber, die in Werkstätten oder zur Anhebung von Fahrzeugen verwendet werden, basieren auf Volumenänderungsarbeit. Durch das Pumpen von Hydraulikflüssigkeit wird Druck erzeugt, der dann dazu verwendet wird, das Volumen eines Kolbens zu ändern und somit das Gewicht anzuheben.
Türschließer: Türschließer in öffentlichen Gebäuden oder Geschäften verwenden oft hydraulische Mechanismen, um Türen zu schließen. Dies geschieht durch Volumenänderungsarbeit, indem die Hydraulikflüssigkeit komprimiert wird.
Staubsauger: Staubsauger arbeiten, indem sie Luft ansaugen und dann die Luft durch einen Filter leiten. Dies erfordert Volumenänderungsarbeit, um die Luft zu komprimieren und sie dann wieder zu expandieren, wenn sie durch den Filter geht.

Volumenänderungsarbeit ohne Umgebungsdruck

Zur Veranschaulichung der Volumenänderungsarbeit betrachten wir einen durch einen Kolben geschlossenen Zylinder (geschlossenes System) mit einem näherungsweise idealen Gas:

Volumenänderungsarbeit, Wärmelehre, Zylinder, Kolben, ideales Gas

In der obigen Grafik siehst du einen mit Gas gefüllten geschlossenen Zylinder. Das Gas weist einen gewissen Druck p auf, welcher gegen die Kolbenwand mit der Querschnittsfläche A drückt. Wird der Kolben mit der Kraft F(s) nach rechts bewegt, so drückt sich die Querschnittsfläche A entlang des Weges s gegen den Druck p(s). Das führt dazu, dass sich das Volumen, welches das Gas einnimmt, verringert.

Betrachten wir zunächst die Sicht von außen und die am Kolben von der Kraft F entlang des Weges s verrichtete Arbeit:

Volumenänderungsarbeit

(1) $\Delta W_V = \int_1^2 F(s) \cdot s$

Die Kraft F entlang des Weges s verrichtet die Volumenänderungsarbeit W_V. Diese Arbeit ist positiv und wird dem Gas zugeführt. Damit erhöht sich die innere Energie des Gases.

Durch das Zusammendrücken des Kolbens verdichtet sich das Gas und der Druck steigt mit zunehmendem Weg s an. Je weiter der Kolben zusammengedrückt wird, desto größer wird das Gas verdichtet und der Druck p(s) im Zylinder steigt an. Die aufzuwendende Kraft F(s) muss also zunehmen, je weiter der Kolben zusammengedrückt wird. Deswegen sind Kraft F(s) und Druck p(s) abhängig vom Weg s und es muss vom Zustand 1 zum Zustand 2 integriert werden.

Wir können das Ganze auch aus Sicht von Innen betrachten. Der Druck p(s) drückt gegen die Querschnittsfläche A des Kolbens. Wir können den Druck auf die Querschnittsfläche auch als resultierende Kraft angeben:

Resultierende Druckkraft, Volumenänderungsarbeit, Zylinder

Diese innere resultierende Druckkraft ergibt sich dann durch den Druck multipliziert mit der Fläche, auf welcher der Druck wirkt:

$F(s) = p(s) \cdot A$ Kraft gleich Druck mal Fläche

Diese Kraft ist identisch mit der äußeren Kraft. Die innere Kraft F(s) steigt an, je weiter der Kolben zusammengedrückt wird, weil das Gas verdichtet wird und damit der Druck p(s) mit zunehmendem Weg s im Zylinder ansteigt.

Wir können nun diesen Ausdruck in der obigen Gleichung (1) ersetzen:

(2) $\Delta W_V = \int_1^2 p(s) \cdot A \cdot s$ Volumenänderungsarbeit

Volumenänderung

Durch das Verschieben des Kolbens, wird das Gas verdichtet und das Volumen reduziert. Betrachten wir die Volumenänderung vom Zustand 1 zum Zustand 2:

Volumenänderung

$\Delta V = V_2 - V_1$

Diese Volumenänderung ist bei einer Verdichtung des Gases negativ, weil das Volumen im Zustand 2 kleiner ist, als im Zustand 1.

Die Volumenänderung ΔV ist nichts anderes als der zurückgelegte Weg des Kolbens multipliziert mit der Querschnittsfläche A:

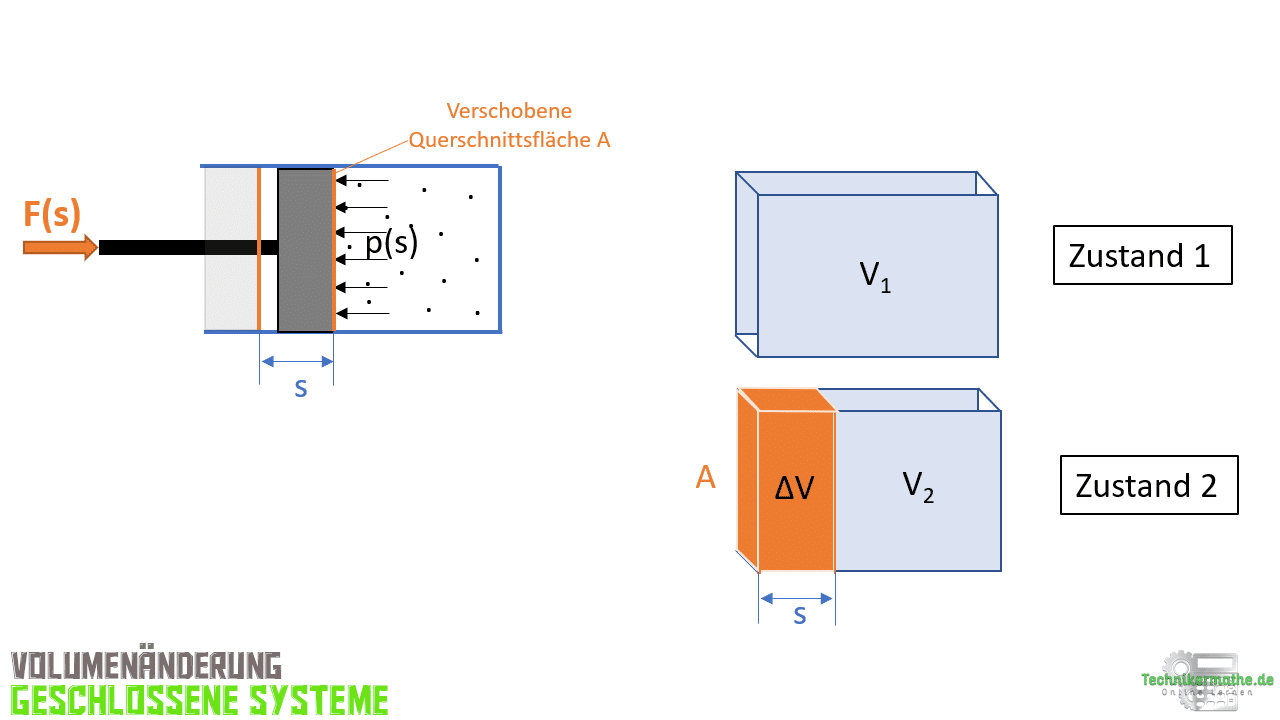
Volumenänderung, Volumenänderungsarbeit (Geschlossene Systeme)

Wir sehen in der obigen Grafik, dass die Volumenänderung gleich Fläche A mal Weg s ist:

$\Delta V = A \cdot s$

Wir können den Ausdruck in Gleichung (2) ersetzen und erhalten:

Volumenänderungsarbeit

(3) $\Delta W_V = -\int_1^2 p(V) \cdot dV$

Das Minuszeichen gilt der Volumenänderung ΔV. Wird der Kolben zusammengedrückt, so verringert sich das Volumen. Die Volumenänderung von Zustand 1 zu Zustand 2 ist also negativ. Es würde also ohne Minuszeichen in der Gleichung ein negativer Wert resultieren. Da die Arbeit dem System aber zugeführt wird (plus) muss hier das Minuszeichen berücksichtigt werden, damit das Ergebnis am Ende positiv ist.

++Beispiel: Volumenänderungsarbeit++

Beispiel!

Gegeben sei ein ideales Gas, welches sich in einem Zylinder befindet und den Druck von p = 180.000 Pa aufweist. Vor der Kompression (Verdichten des Gases) beträgt das Volumen V₁ = 4m³. Nach dem Zusammendrücken des Kolbens, beträgt das Volumen noch V₂ = 3,8m³. Der Druck sei über den gesamten Weg konstant.

Wir wollen nun die Volumenänderungsarbeit berechnen, die dem System zugeführt wird.

Wir haben drei Gleichungen für die Volumenänderungsarbeit gegeben und verwenden diejenige, für welche wir die Größen zur Berechnung gegeben haben.

Gegeben:

$V_1 = 4m^3$

$V_2 = 3,8m^3$

$p_1 = p_2 = p = 180.000 Pa$

Gesucht:

$W_V$

Wir können die folgende Gleichung (3) heranziehen:

$\Delta W_V = -\int_1^2 p(V) \cdot dV$

Die Volumenänderung ergibt sich wie folgt:

$\Delta V = V_2 - V_1 = 3,8m^3 - 4m^3 = -0,2m^3$

Da wir einen konstanten Druck gegeben haben, dieser sich also über den Weg s nicht ändert, fällt das Integral weg:

$\Delta W_V = -p \cdot \Delta V$

Einsetzen der gegebenen Werte:

$\Delta W_V = -180.000 Pa \cdot (-0,2m^3) = 36.000 J$

Die zugeführte Volumenänderungsarbeit beträgt 36.000 Joule. Die innere Energie des betrachteten System erhöht sich also um 36.000 J.

Volumenänderungsarbeit mit Umgebungsdruck – Erklärung

Befindet sich der Zylinder mit dem eingeschlossenen Gas im Vakuum, so ist der Umgebungsdruck nicht vorhanden (p_u = 0). Bei einer Kompression wird dem eingeschlossenen Gas die gesamte Volumenänderungsarbeit zugeführt. Bei einer Expansion wird die gesamte Volumenänderungsarbeit an der Kolbenstange abgeführt und als Nutzarbeit abgenommen werden.

Befindet sich der Zylinder hingegen in einer Umgebung mit dem Umgebungsdruck p_u > 0, z. B. auf der Erde mit dem Atmosphärendruck 101.325 Pa, so verringert sich in beiden Fällen (Expansion und Kompression) die Volumenänderungsarbeit im Vergleich zum Vakuum.

Nutzarbeit, Verschiebearbeit, Volumenänderungsarbeit

Bei einer Kompression (Volumenverkleinerung) gibt der Umgebungsdruck (z.B. der Atmosphärendruck) über die Kolbenrückseite Volumenänderungsarbeit an den Zylinder ab. Der Umgebungsdruck “hilft” also, den Kolben zusammenzudrücken und vermindert damit den Arbeitsaufwand an der Kolbenstange (siehe obige Grafik).

Bei einer Expansion (Volumenvergrößerung) wird ein Teil der vom Zylinder abgeführten Volumenänderungsarbeit dazu verwendet, den Umgebungsdruck auf der Kolbenrückseite zu verdrängen. Das bedeutet, dass nicht die gesamte Volumenänderungsarbeit als Nutzarbeit zur Verfügung steht.

Wir können die Arbeit, die durch den Umgebungsdruck p_u an der Kolbenstange geleistet wird als Verschiebearbeit W_u bezeichnen:

Verschiebearbeit

$W_{u12} = -\int_{V_1}^{V_2} p_u(V) dV$

Bei einem konstanten Umgebungsdruck (z.B. dem Atmosphärendruck), können wir direkt integrieren (p_u(V) = p_u = const):

$W_{u12} = -p_u \cdot [V]_{V_1}^{V_2}$

Mit Einsetzen der Grenzen ergibt sich dann die Verschiebearbeit bei konstantem Umgebungsdruck:

Verschiebearbeit bei konstantem Umgebungsdruck

$W_{u12} = -p_u \cdot (V_2 - V_1)$

Die Verschiebearbeit muss bei der Berechnung der gesamten Volumenänderungsarbeit berücksichtigt werden. Sie vermindert sowohl bei der Expansion als auch bei der Kompression die Volumenänderungsarbeit im Vergleich zum Vakuum. Damit vermindert sich auch die tatsächliche gewinnbare Nutzarbeit W_n (bei der Expansion) bzw. die aufzuwendende Nutzarbeit W_n (bei der Kompression):

Volumenänderungsarbeit mit Umgebungsdruck

$W_{V12} = -\int_1^2 p(V) \cdot dV$ Gesamte Volumenänderungsarbeit

$W_{V12} = W_{n12} - p_u \cdot (V_2 - V_1)$

$-\int_1^2 p(V) \cdot dV = W_{n12} - p_u \cdot (V_2 - V_1)$

Die gesamte Volumenänderungsarbeit W_V enthält die Nutzarbeit W_n und die Verschiebearbeit. Die bei der Expansion tatsächlich nutzbare Arbeit (=Nutzarbeit) an der Kolbenstange ergibt sich wie folgt:

Nutzarbeit

$W_{n12} = -\int_1^2 p(V) \cdot dV + p_u \cdot (V_2 - V_1)$

Ist ein Vakuum gegeben, so ist die Nutzarbeit und die gesamte Volumenänderungsarbeit identisch, da die Verschiebearbeit wegfällt:

$W_{n12} = W_{V12} = -\int_1^2 p(V) \cdot dV$

Merk’s dir!#

Die gesamte Volumenänderungsarbeit W_V wird mit dem Absolutdruck p_abs des Gases im Zylinder bestimmt:

$W_{V12} = -\int_1^2 p_{abs}(V) \cdot dV$

pV-Diagramm: Verschiebearbeit und Nutzarbeit

In der nachfolgenden Grafik sieht du ein pV-Diagramm mit abgeführter Volumenänderungsarbeit (Expansion):

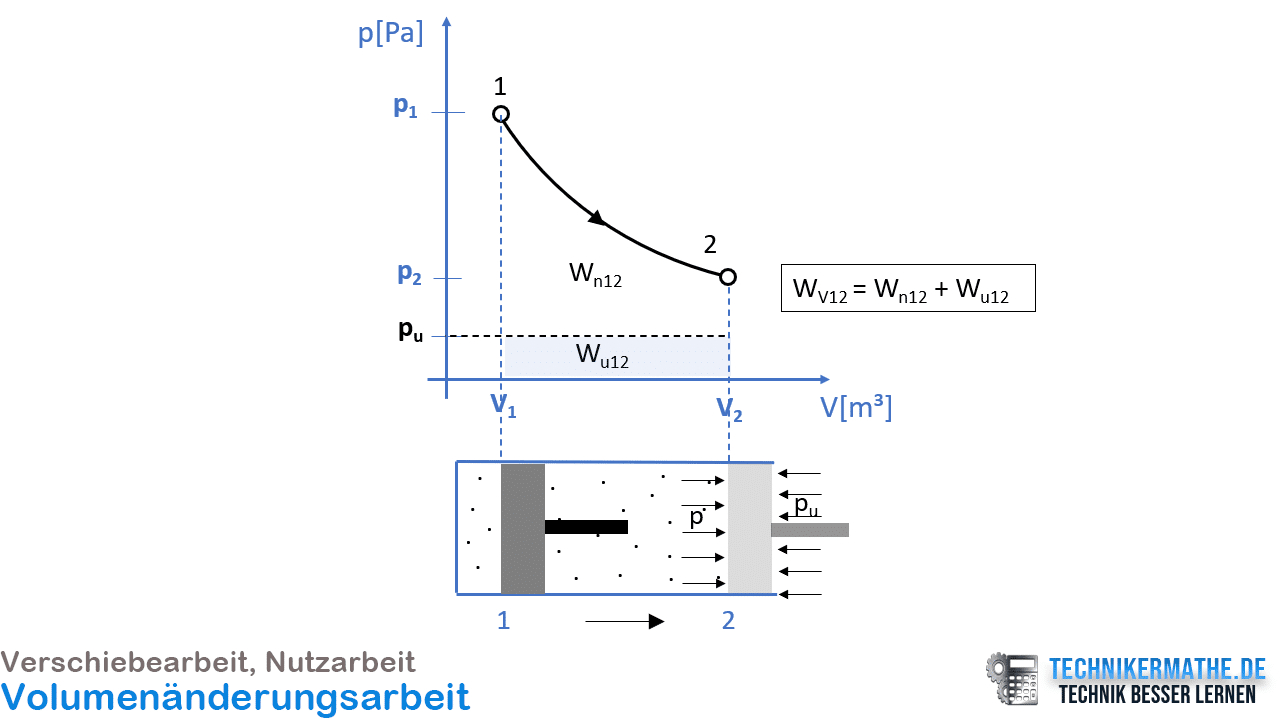
Verschiebearbeit, Nutzarbeit, Volumenänderungsarbeit

Die Volumenänderungsarbeit lässt sich in die Nutzarbeit W_n und Verschiebearbeit W_u aufteilen, sofern ein Umgebungsdruck p_u vorhanden ist. In der obigen Grafik siehst du den Verlauf der Zustandsänderung im pV-Diagramm bei einer Expansion dargestellt. Von Zustand 1 zu Zustand 2 erhöht sich das Volumen und der Druck sinkt. Die Verschiebearbeit W_u wird an die Umgebung abgegeben und kann nicht weiter genutzt werden. Damit verbleibt der Teil der Volumenänderungsarbeit, der als Nutzarbeit W_n für weitere Prozesse verwendet werden kann.

++Beispiel: Volumenänderungsarbeit, Verschiebearbeit, Nutzarbeit++

Aufgabenstellung

Ein Gasbehälter hat eine kreisförmige Grundfläche mit einem Radius r = 5 m und eine Höhe von h = 15 m. Er wird durch eine höhenverschiebbare Scheibe gasdicht abgeschlossen.

Die Scheibe hat eine Masse von m_scheibe = 46.450 kg, der Luftdruck beträgt p_L = 1000 mbar. Durch Sonneneinstrahlung vergrößert sich das Gasvolumen bei gleichbleibendem Luft- und Gasdruck und die Scheibe hebt sich reibungsfrei und sehr langsam um s = 0,5 m.

a) Wie groß ist die gegen den Luftdruck verrichtete Arbeit?

b) Wie groß ist die Volumenänderungsarbeit?

c) Stelle die Zustandsänderung in einem p-V-Diagramm dar und trage auch die gegen den Luftdruck verrichtete Arbeit sowie die Volumenänderungsarbeit ein!

d) Wie groß ist die Änderung der inneren Energie, wenn die Sonneneinstrahlung 44.740 kJ beträgt?

Lösung der Aufgabe

a) Verschiebearbeit

Zunächst sollen wir die gegen den Luftdruck verrichtete Arbeit berechnen. Hierbei handelt es sich um die Verschiebearbeit W_u:

$W_{u12} = -p_u \cdot (V_2 - V_1) = -p_u \cdot \Delta V$

Der Umgebungsdruck p_u ist hier der Luftdruck. Wir müssen diesen noch in Pascale (SI-Einheit des Drucks) umrechnen:

$p_u = p_L = 1.000 mbar = 1 bar = 100.000 Pa$

Als nächstes benötigen wir die Volumenänderung von Zustand 1 zum Zustand 2. Diese ist in der Aufgabenstellung nicht angegeben, dafür aber der Weg s und die Querschnittsfläche. Hieraus können wir das Volumen berechnen:

$\Delta V = A \cdot \Delta s = \pi \cdot r^2 \cdot \Delta s$

Wir haben eine kreisförmige Querschnittsfläche gegeben, weshalb wir hier die Fläche eines Kreises verwenden. Einsetzen der in der Aufgabenstellung gegebenen Werte führt uns auf:

$\Delta V = \pi \cdot (5m)^2 \cdot 0,5m = 39,27 m^3$

Wir können nun die Volumenänderung und den Luftdruck eingeben:

$W_{u12} = -p_u \cdot \Delta V = -100.000 Pa \cdot 39,72 m^3 = -3.927.000 Pa m^3$

Die Einheit Pascale mal Kubikmeter entspricht der Einheit Joule:

$\frac{kg m^2}{s^2} \cdot m^3 = \frac{kg m^2}{s^2} = J$

Es ergibt sich demnach:

$W_{u12} = -3.927.000 J = -3,927 MJ$

Die Verschiebearbeit ist negativ, weil sie von der Kolbenstange abgegeben wird.

b) Volumenänderungsarbeit

Die Volumenänderungsarbeit ist die gesamte Arbeit, die an der Kolbenstange abgegeben wird. Da ein Umgebungsdruck gegeben ist, setzt sich diese aus der Nutzarbeit und der Verschiebearbeit zusammen und wird wie folgt berechnet:

$W_{V12} = -\int_1^2 p(V) \cdot dV$

In dieser gesamten Volumenänderungsarbeit ist die Nutzarbeit und die Verschiebearbeit enthalten.

Wir wollen nun die Volumenänderungsarbeit berechnen. Die Volumenänderung ΔV haben wir bereits berechnet. Wir müssen noch den Druck p(V) ermitteln, um die obige Gleichung anwenden zu können. Über die Zustandsgleichung des idealen Gases können wir diesen leider nicht berechnen, da wir zu wenig Größen gegeben haben. So fehlt uns nicht nur der Druck p im Kolben sondern auch die Temperatur. Das sind zwei unbekannte Größen. Wir müssen demnach in der Aufgabenstellung nach anderen Werten schauen.

Wir haben in der Aufgabenstellung z.B. die Masse der Scheibe gegeben. Diese wird durch die Volumenvergrößerung um 0,5 m angehoben. Wir können uns also die Frage stellen:

Wie viel Kraft ins nötig, um die Scheibe anzuheben?

Die Scheibe wird angehoben. Das bedeutet, dass hier gegen die Schwerkraft gearbeitet wird und wir deswegen sehr leicht die Kraft berechnen können, die dazu notwendig ist:

$F_{scheibe} = m_{scheibe} \cdot g = 46.450 kg \cdot 9,81 \frac{m}{s^2} = 455.674,5 N$

Wir haben also die gesamte Kraft berechnet, die zum Anheben der Scheibe notwendig ist, damit sich die Volumenvergrößerung ergibt. Hierbei handelt es sich um diejenige Kraft im Zustand 2, die aufgewendet werden muss, um die angehobene Scheibe in Position zu halten. Sie wirkt gegen den herrschenden Überdruck im Gasbehälter. Wir können aus dieser Kaft also den Überdsruck im Gasbehäter berechnen:

$p_e = \frac{F}{A} = \frac{455.674,5 N}{\pi \cdot (5m)^2} = 5.802 Pa$

Für die Berchnung der Volumenänderungsarbeit benötigen wir aber den Absolutdruck. Diesen berechnen wir aus der folgenden Formel:

$p_{abs} = p_e + p_u = 5.802 Pa + 100.000 Pa = 105.802 Pa$

Wir können nun die Volumenänderungsarbeit berechnen:

$W_{V12} = -\int_1^2 p(V) \cdot dV$

Da der Druck laut Aufgabenstellung konstant bleibt, gilt:

$W_{V12} = -\int_1^2 p \cdot dV$

$W_{V12} = -p \cdot (V_2 - V_1)$

Einsetzen der Werte:

$W_{V12} = -105.802 Pa\cdot 39,27 m^3 = -4.154.844,54 J = -4,155 MJ$

Die gesamte Volumenänderungsarbeit, die dem Zylinder abgeführt (Minuszeichen) wird, beträgt 4,155 MJ.

c) pV-Diagramm

In der folgenden Grafik siehst du das dazugehörige pV-Diagramm der Expansion. Vom Zustand 1 zum Zustand 2 bleibt der Druck p konstant und das Volumen V erhöht sich. Damit ergibt sich eine horizontale Gerade. Die Volumenänderungsarbeit V_W entspricht der Fläche unterhalb der Geraden. Diese Fläche wird aufgeteilt in die Nutzarbeit W_n (die Arbeit, die weiter verwendet werden kann) und die Verschiebearbeit W_u (die Arbeit zum verschieben des Luftdrucks):

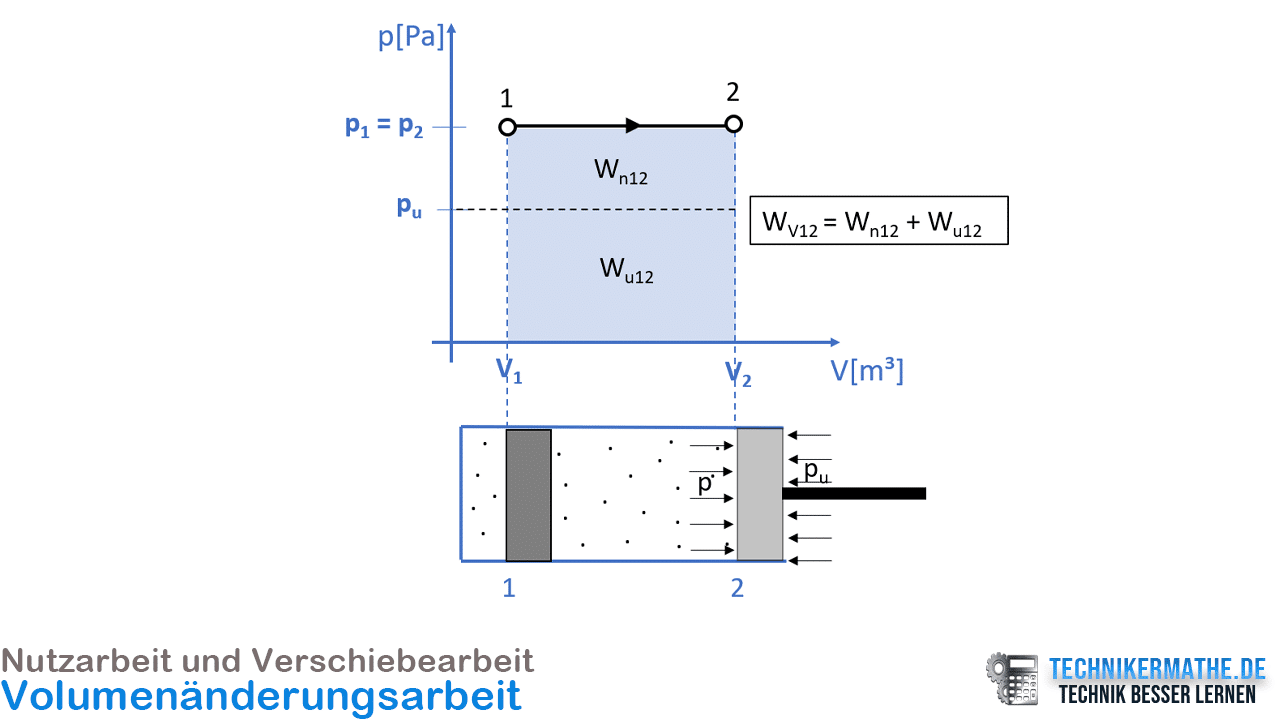
d) Innere Energie

Die Änderung der inneren Energie in einem geschlossenen System wird wie folgt berechnet:

$\Delta U = \Delta W + \Delta Q$

Von Zustand 1 zu Zustand 2 ergibt sich dann:

$U_{12} = W_{V12} + Q_{12}$

Wir haben bereits die Arbeit ΔW berechnet. Das ist nichts anderes als die gesamte Volumenänderungsarbeit W_V12= -4,154 MJ (in der folgenden Lerneinheit betrachten wir noch Dissipationsarbeit, die hier aber nicht gegeben ist):

$U_{12} = -4,154 MJ + Q_{12}$

Die Änderung der Wärmemenge von Zustand 1 zu Zustand 2 ist in der Aufgabenstellung mit Q₁₂ = 44.740 kJ. Die Wärme wird dem Zylinder zugeführt, weshalb wir diese positiv berücksichtigen. Wir müssen die beiden Einheiten kJ und MJ auf eine Einheit bringen:

$W_{V12} = -4,154 MJ = -4.154 kJ$

Wir setzen die beiden Werte in die Formel für die Änderung der inneren Energie ein:

$U_{12} = -4.154 kJ + 44.740 kJ = 40.586 kJ$

Die innere Energie nimmt von Zustand 1 zu Zustand 2 um 40.586 kJ zu.

Über Technikermathe

Tausende interaktive Übungsaufgaben

Übungsbereich

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Das erwartet dich!

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Auszüge aus unserem Kursangebot!

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

building 4794329 1280 — TM1 (Technische Mechanik – Kurs)

scientist 6621069 1280 — WT3 (Werkstoffprüfung – Kurs)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 26 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++