[ME1] Torsionsbeanspruchung (Torsion) [Erklärung, Beispiele, Berechnung, Videos]

In diesen Kursabschnitt befassen wir uns ausführlich mit der Torsion (Torsionsbeanspruchung).

Für ein optimales Verständnis helfen dir einige anschauliche Beispiele und abschließende, umfangreiche Abbildungen zu dem Thema, sowie ein zusammenfassender Videoclip.

Torsionsbeanspruchung – Grundlagen

Eine Torsion ist immer dann gegeben wenn an oder in Maschinenbauteilen Kräfte, Momente oder Kräftepaare wirken, deren Wirkungslinie nicht mit der Balkenachse oder Trägheitsebene übereinstimmt. Ferner lässt sich die Torsion weiter unterscheiden in

Reine Torsion &
Gängige Torsion

Reine Torsion

Die reine Torsion ist eine mechanische Belastung, bei der ein Körper um seine Achse verdreht wird, ohne dass dabei Biege- oder Scherkräfte auftreten.

Hier sind einige Beispiele für reine Torsion:

Beispiele!

Schraubendreher: Wenn Sie einen Schraubendreher verwenden, um eine Schraube in ein Material einzudrehen, wird der Schaft des Schraubendrehers einer reinen Torsionsbelastung ausgesetzt.
Torsionsstab: Ein langer, zylindrischer Stab, der an einem Ende fest eingespannt ist und am anderen Ende eine Drehmomentkraft erfährt, ist ein klassisches Beispiel für reine Torsion. Das bekannteste Beispiel ist die Torsion in einem elastischen Stab, wie sie in der Torsionsprüfung von Materialien verwendet wird.
Torsionsfeder: Eine Spiralfeder, wie sie in mechanischen Vorrichtungen und in der Technik verwendet wird, unterliegt einer reinen Torsionsbelastung, wenn sie verdreht wird, um eine Federkraft zu erzeugen.
Torsionspendel: Ein Torsionspendel besteht aus einem dünnen Draht oder einem dünnen Stab, an dem ein Massenelement befestigt ist. Wenn das Massenelement aus seiner Gleichgewichtslage verdreht wird, erzeugt die Rückstellkraft des Drahts oder Stabs eine Schwingung um die Torsionsachse.

Diese Beispiele veranschaulichen Situationen, in denen reine Torsion auftreten kann. Es ist wichtig anzumerken, dass reine Torsion in der Realität selten vorkommt, da Biege- und Scherkomponenten oft mit der Torsion verbunden sind.

Gängige Torsion

Zumeist liegt eine Überlagerung mit Biegemomenten und Querkräften vor.

Hier sind einige Beispiele für Situationen, in denen es nicht nur um reine Torsion geht:

Beispiele!

Biegetorsion: Bei einer Kombination aus Biegung und Torsion werden sowohl Biegemomente als auch Torsionsmomente auf ein Bauteil ausgeübt. Ein Beispiel dafür ist eine Welle, die sowohl durch Biegung als auch durch Torsion belastet wird, wie es bei einer Antriebswelle der Fall ist.
Torsionsbiegung: In einigen Fällen kann die Torsion zu einer Biegung führen. Ein Beispiel dafür ist ein Stab, der an einem Ende verdreht wird, wodurch eine Torsionsbelastung erzeugt wird, die sich entlang des Stabs ausbreitet und zu einer Krümmung führt.
Kombinierte Belastungen: Oft treten verschiedene Belastungen gleichzeitig auf, wie zum Beispiel Zug, Druck, Biegung und Torsion. Diese kombinierten Belastungen treten häufig in komplexen Strukturen wie Brücken, Gebäuden oder Flugzeugrümpfen auf.
Scherbelastung: Scherung ist eine andere Form der Belastung, bei der Kräfte parallel zur Querschnittsfläche eines Materials wirken. Scherbelastungen treten oft zusammen mit Torsionsbelastungen auf und spielen eine Rolle bei der Analyse von Balken, Wellen und anderen strukturellen Elementen.

Torsion – Beispiele im Alltag

Hier sind einige Beispiele für Torsion, die im Alltag vorkommen:

Beispiele!

Türgriffe: Wenn du eine Tür öffnest, übst du eine Torsionskraft auf den Türgriff aus, um ihn zu drehen und die Tür zu öffnen.
Schraubverschlüsse: Beim Öffnen oder Schließen von Schraubverschlüssen, wie zum Beispiel bei einem Deckel auf einem Glas oder einer Flasche, wird Torsion angewendet, um den Verschluss zu lösen oder festzuziehen.
Spielzeugkreisel: Ein Spielzeugkreisel funktioniert durch Torsion. Durch das Verdrehen des Griffs oder der Schnur wird eine Torsionskraft erzeugt, die den Kreisel rotieren lässt.
Korkenzieher: Beim Verwenden eines Korkenziehers zum Öffnen einer Weinflasche wird eine Torsionskraft ausgeübt, um den Korken aus der Flasche zu ziehen.
Haarspangen: Beim Befestigen von Haarspangen oder Haarklammern wird oft Torsion angewendet, um das Haar zu halten.
Schraubendreher: Wenn du einen Schraubendreher verwendest, um eine Schraube einzudrehen oder herauszudrehen, wendest du eine Torsionskraft an, um die Schraube zu drehen.
Sportgeräte: Viele Sportgeräte nutzen Torsion, zum Beispiel beim Golfen wird durch die Drehung des Golfschlägers Torsion erzeugt, um den Ball zu schlagen. Auch beim Tennis, Baseball oder beim Drehen eines Jojos tritt Torsion auf.

Diese Beispiele zeigen, dass Torsion im Alltag häufig vorkommt und in verschiedenen Gegenständen und Handlungen eine Rolle spielt.

Torsion – Anwendungsfälle

In der nächsten Abbildung siehst du hierzu die unterschiedlichen Szenarien für das Auftreten einer Torsion.

Aufgepasst!

In der nachfolgenden Abbildung sind die Stäbe fest an der Wand eingespannt und erlauben somit keine Drehbewegung!

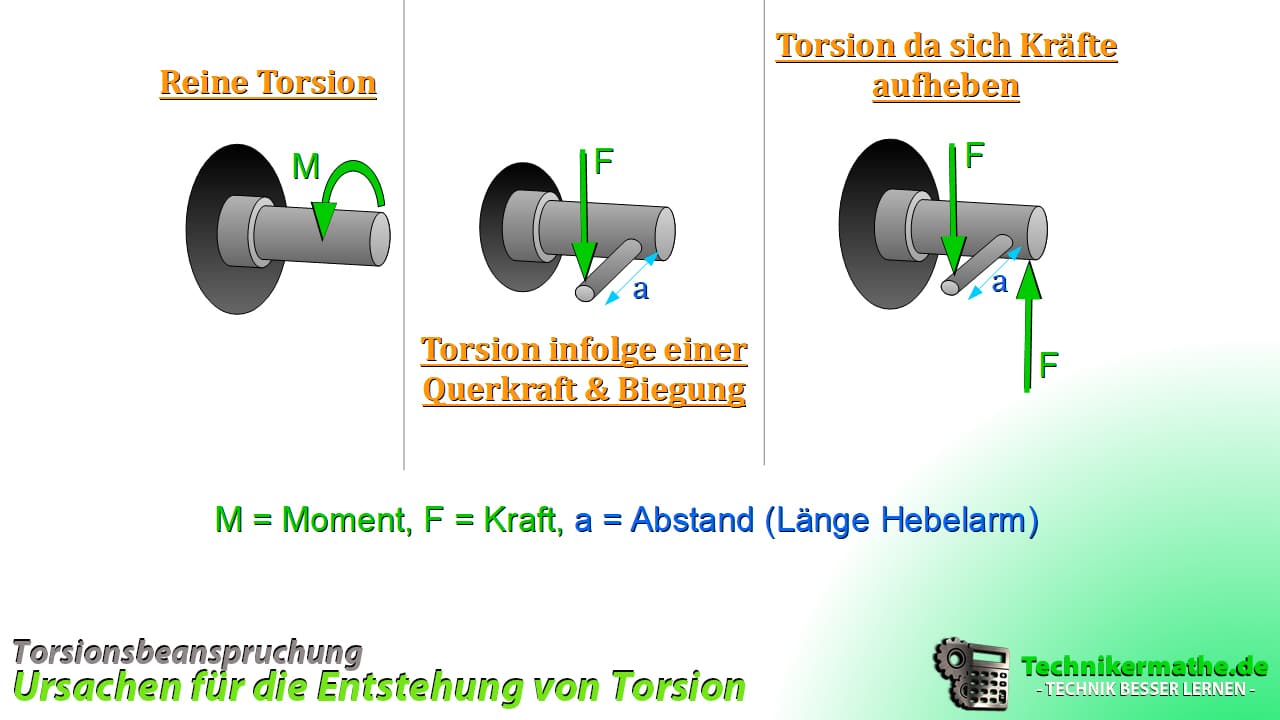
Im ersten Fall wird ein Torsionsmoment eingeleitet, wodurch eine reine Torsion entsteht, da der Stab fest eingespannt ist.
Im zweiten Fall sehen wir eine Kraft 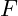$F$ die an einem Hebelarm mit der Länge 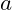$a$ wirkt. Das Produkt aus beiden, also $F \cdot a$ ergibt das Torsionsmoment. Am Anlenkpunkt wirkt dabei eine Querkraft, welche an der Einspannstelle ein Biegemoment erzeugt. Hierbei handelt es sich um einen ungünstigen Fall.
Im dritten Fall können wir durch eine zusätzliche Kraft, die durch die Drehachse der Hauptstruktur geht, die Querkraft und Biegung wieder auf null zwingen (Kräftegleichgewicht wird wieder Null) ohne das Drehmoment wieder auf null zu bringen. Es verbleibt wieder nur Torsion

Torsion – Ablaufschema zur Torsionsberechnung

Funktionsermittlung

Er handelt sich also um einen Hebel zur Drehmomenterzeugung. Beansprucht wird dieser durch eine außermittige Last. Ein Beispiel hierfür ist der Radmutterschlüssel.

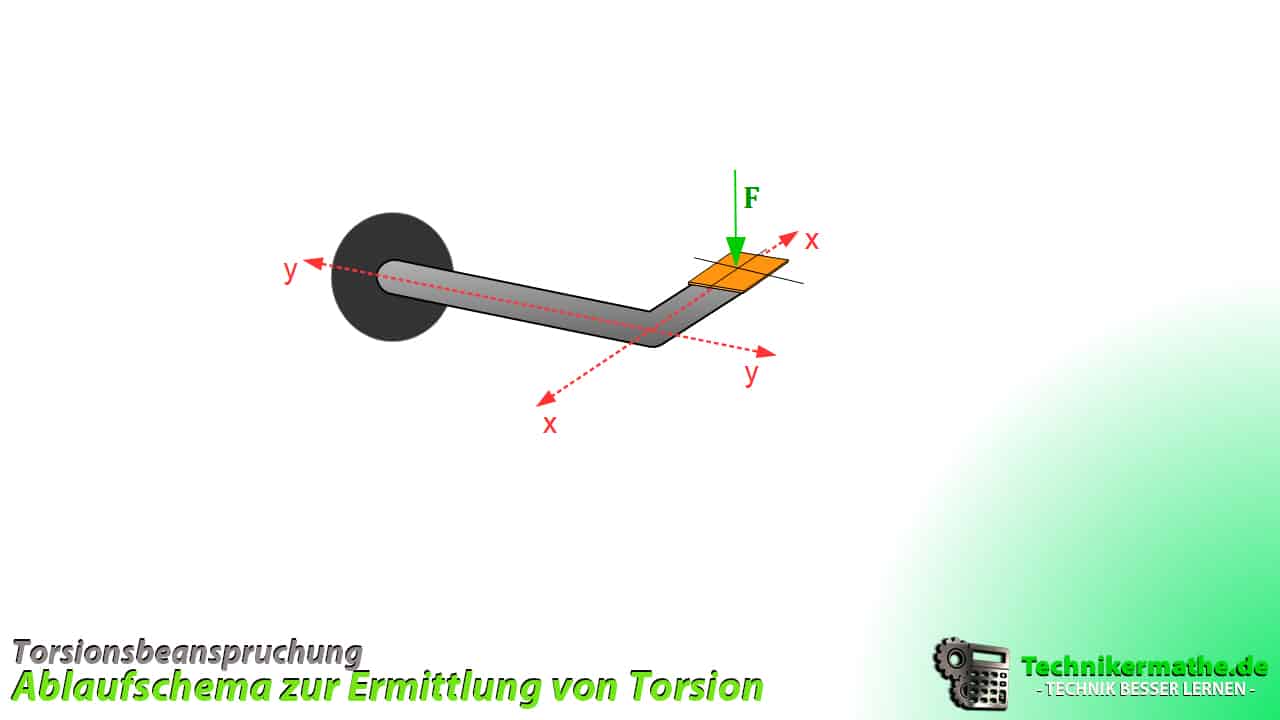
Torsionsbeanspruchung - Funktionsbestimmung — Torsionsbeanspruchung – Funktionsbestimmung

Größenerfassung

In der nachfolgenden Abbildung ist ein fest eingespannter Stab mit einem Hebelarm (ähnlich einer Türklinke) dargestellt, welcher am Ende des Hebelarms (Bereich 1 mit der Länge a) durch eine Kraft $F$ belastet wird. Auch der Abschnitt zwischen Einspannung und Abknickung (Bereich 2-3 mit der Länge b) stellt einen Hebelarm dar. Der Durchmesser beträgt d.

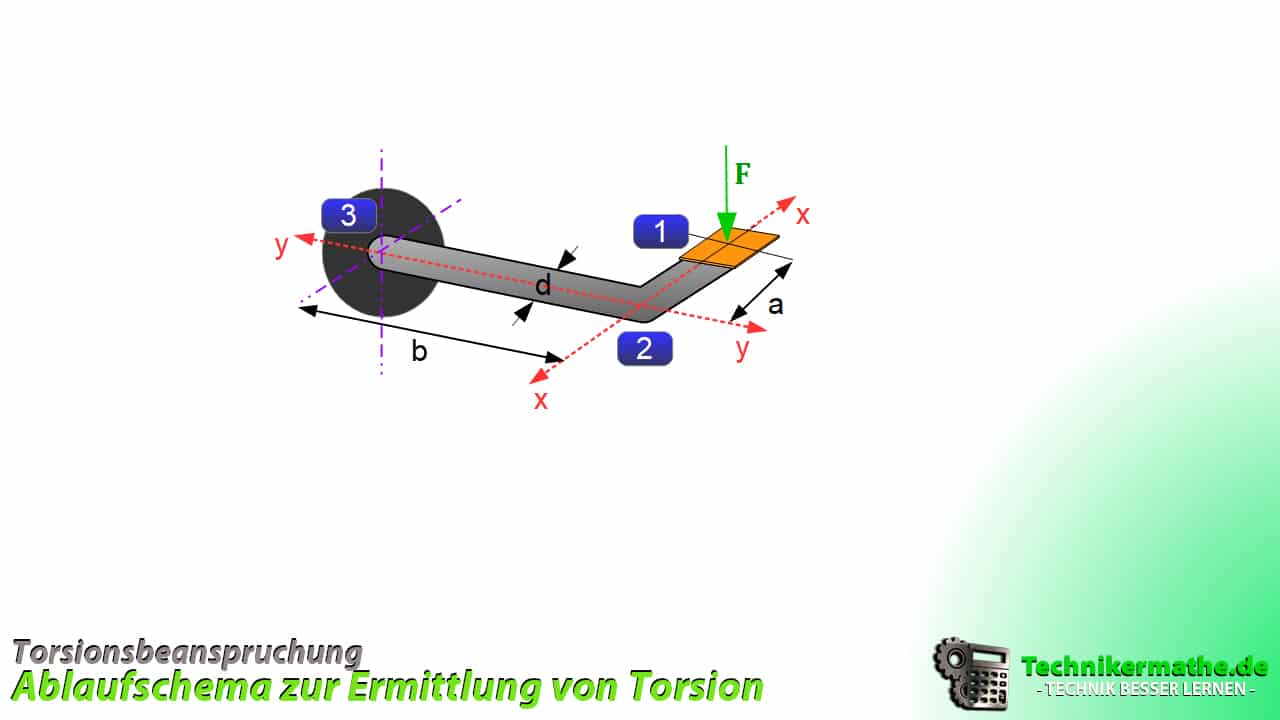
Mechanisches Ersatzbild

Im mechanischen Ersatzbild finden wir zwei Elemente einen Biegebalken und einen Torsionsstab. Der Bereich mit der Länge $b$ ist sowohl eine Biegebeanspruchung als auch einer Torsionsbeanspruchung.

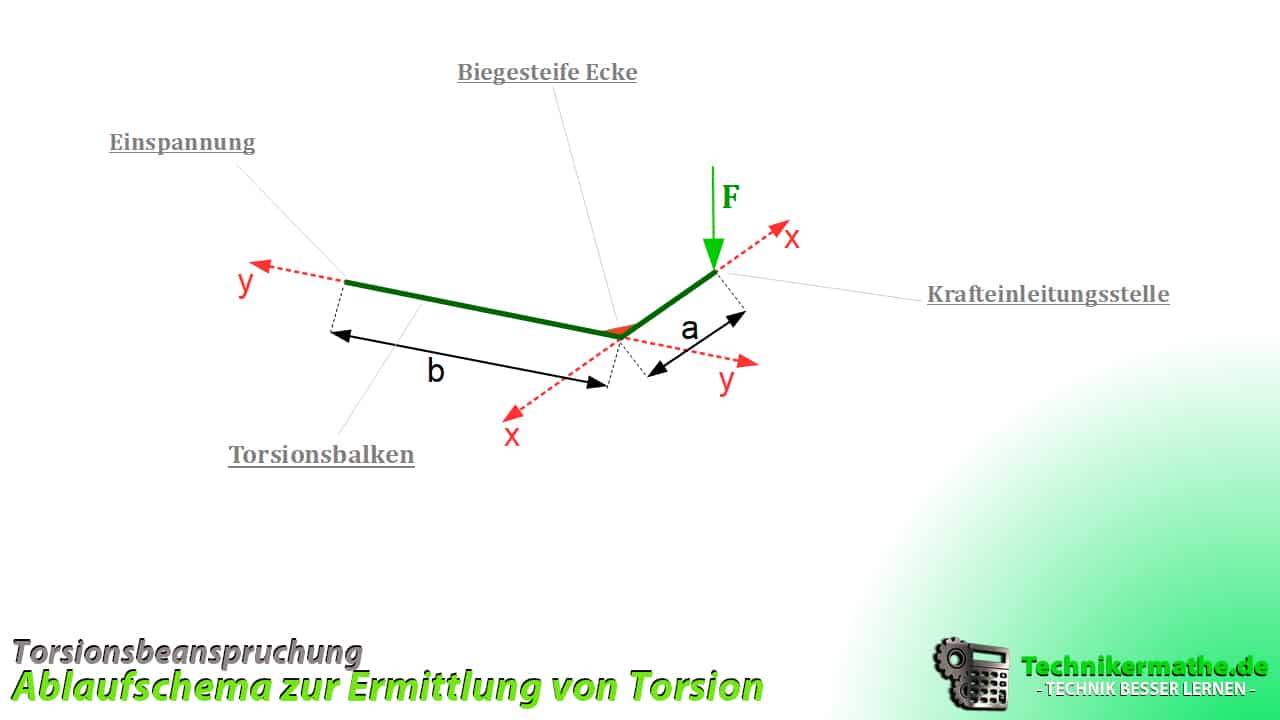
Schnittgrößen ermitteln

Hier legen wir 3 Schnittstellen fest. Wobei wir die Schnittstelle 2 sowohl von rechts als auch von links betrachten müssen. Zudem sei hier erwähnt, dass es sich bei der Schnittstelle 2 um eine biegesteife Ecke handelt (orangene Ausfüllung der Ecke), die Biegemoment übertragen kann. Schnittstelle 1 ist die Krafteinleitungsstelle mit der Querkraft $F$ .

Schnittstelle 1

$N = 0$ [In Achsrichtung (x) wirkt keine Kraft]

$Q = F$ [Kraft F wirkt senkrecht zur Bauteilachse (x)]

$M = 0$ [Es liegt kein Hebelarm vor, daher kein Biegemoment]

$T = 0$ [Es wird hier keine Torsion eingeleitet]

Schnittstelle 2 (rechts)

$N = 0$ [In Achsrichtung (x) wirkt keine Kraft]

$Q = F$ [Kraft F wirkt senkrecht zur Bauteilachse (x)]

$M = F \cdot a$ [Es liegt ein Hebelarm vor, daher ein Biegemoment]

$T = 0$ [Es wird hier keine Torsion eingeleitet]

Schnittstelle 2 (links)

$N = 0$ [In Achsrichtung (y) wirkt keine Kraft]

$Q = F$ [Kraft F wirkt senkrecht zur Bauteilachse (y)]

$M = 0$ [Es liegt kein Hebelarm vor, daher kein Biegemoment]

$T = F \cdot a$ [Es wird hier eine Torsion eingeleitet]

Schnittstelle 3

$N = 0$ [In Achsrichtung (y) wirkt keine Kraft]

$Q = F$ [Kraft F wirkt senkrecht zur Bauteilachse (y)]

$M = F \cdot b$ [Es liegt ein Hebelarm (b) vor, daher ein Biegemoment]

$T = F \cdot a$ [Es wird hier eine Torsion eingeleitet]

Visualisierung der Kräfte

Im letzten Schritt visualisieren wir die Kräfte $Q, M_b, T$ , genauer gesagt der Verläufe von der Schnittstelle 1 bis 3.

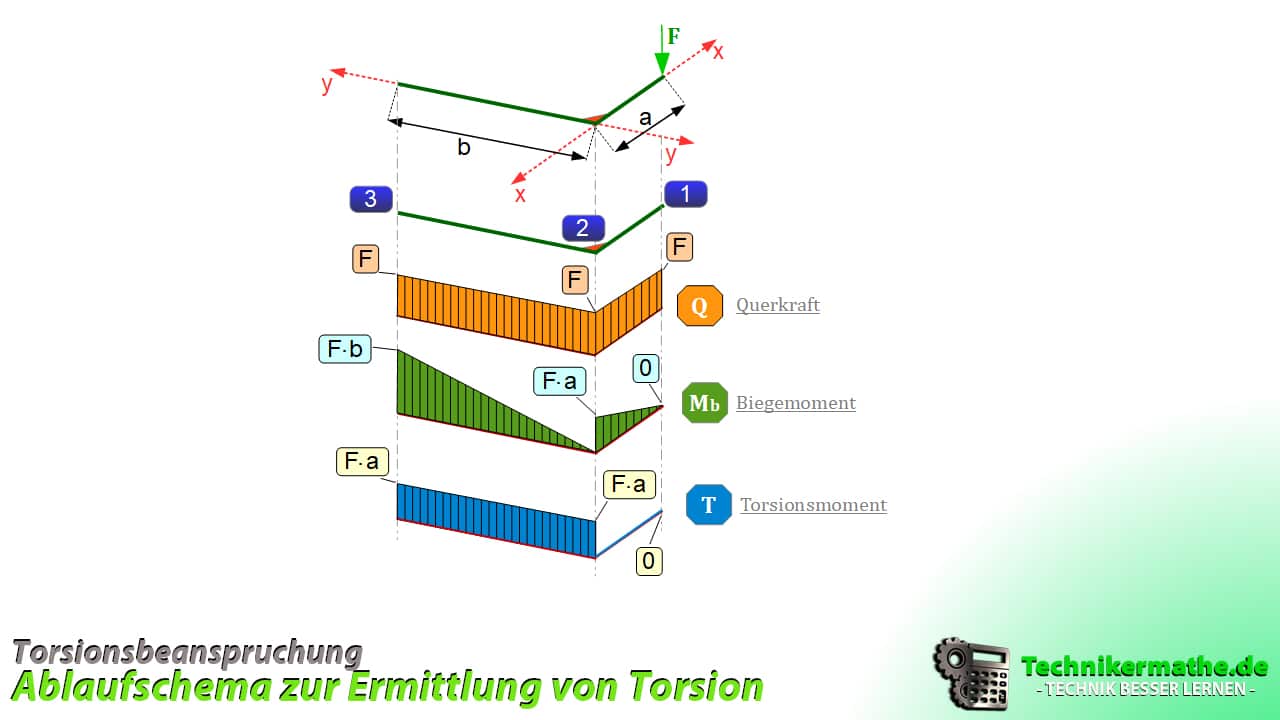
Torsionsbeanspruchung - Kraftverläufe Q, Mb, T — Torsionsbeanspruchung – Kraftverläufe Q, Mb, T

Merk’s dir!

Schaut man sich die Verläufe genauer an, so fällt auf, dass die kritische Stelle die Einspannstelle (3) ist. Daher sollten die Belastungen und Spannungen an dieser Stelle berechnet werden.

Torsion – Formel

Als Modellfall betrachten wir nun den geraden Torsionsstab mit einem Kreis- oder Kreisringquerschnitt.

Suchen wir uns nun eine beliebige Stelle des Stabes x so ergibt sich nachfolgende Gleichung:

$\tau_t = \frac{T}{J_p} \cdot r$

Kennzahlen

$\tau_t =$ Schubbeanspruchung für Torsion
$T =$ Torsionsmoment
$J_p = J_y + J_z =$ Polares Flächenträgheitsmoment des Kreisquerschnitts
$r = \frac{d}{2}$ Radius

An der Außenfaser liegt die höchste Beanspruchung. Analog zur Biegebeanspruchung führen wir nun ein Widerstandsmoment ein. Uns interessiert lediglich der Wert an der Außenfaser, da dieser dem Maximalwert darstellt. Kleinere Beanspruchungen sind hingegen unkritisch.

$\tau_{t, max} = \frac{T}{W_t} = \frac{T}{W_p} \le \tau_{zul}$

Kennzahlen

$\tau_{t, max} =$ maximale Schubbeanspruchung für Torsion
$T =$ Torsionsmoment
$W_t = W_p = W_y + W_z =$ Polares Widerstandsmoment
$\tau_{zul} =$ maximal zulässige Schubbeanspruchung für Torsion

wobei

$W_p = \frac{J_p}{r}$

Torsion – Gestaltungsarten

Abschließend stellen wir uns die Frage: Welcher Querschnitt ist optimal bei einer Torsionsbeanspruchung?

War das doppel-T-Träger-Profil (I-Profil) noch die beste Wahl bei einer Biegebeanspruchung, so ist dieser hier bei einer Torsionsbeanspruchung eher ungünstig. Denn betrachten wir erneut den vorangegangenen Fall mit der Profilwelle, so hat sich gezeigt, dass die höchste Belastung an der Außenfaser besteht. Logischerweise, sollte sich hier das meiste Material befinden. Daher sind geschlossene Querschnitte wesentlich steifer als offene Querschnitte bei gleichem Materialaufwand.

Merk’s dir!

Das Verhältnis zwischen dem Flächenträgheitsmoment

[ $I_{t, quadrat}$

] zu [ $I_{t, I-Profil}$

]

ist [ $77$ ] zu [ $1$ ].

Optimal sind runde Querschnitt gefolgt von quadratischen Querschnitten. Es sollte daher nach Möglichkeit eine Anpassung an einen Kreisquerschnitt vorgenommen werden, beispielsweise durch Abrunden der Ecken eines quadratischen Querschnitts.

In Bezug auf die Torsionssteifigkeit sind geschlossene, hohle Querschnitt bei gleichem Gewicht am steifsten.

Was soll es denn sein?…

Treten sowohl Biegebeanspruchungen als auch Torsionsbeanspruchungen auf, so sollte die Wahl zwischen einem I-Träger-Profil oder einem Kreisprofil davon abhängig gemacht werden, welche Anteile überwiegen.

Was kommt als Nächstes?

Nachdem wir uns mit der Torsion als Beanspruchungsart befasst haben und du im Vorfeld die Beanspruchungsarten Zug, Druck und Biegung ausführlich kennengelernt hast, gehen wir im kommenden Kurstext auf die zusammengesetzten Beanspruchungen ein. Eine zusammengesetzte Beanspruchung liegt immer dann vor, wenn mehrere, der oben aufgeführten Beanspruchungen gemeinsam auftreten und zusammen wirken.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++