Schraubenverbindung Teil 4 – Der Tragfähigkeitsnachweis

Diese Lerneinheit beinhaltet...

Nachdem wir uns bereits einen guten Überblick zu den Nachgiebigkeiten einer Schraubenverbindung und den notwendigen Berechnungen des Montagezustandes und Betriebszustandes der Schraubenverbindung verschafft haben, schließen wir mit dem vierten Abschnitt Tragfähigkeitsnachweis das Thema Schraubenverbindungen ab.

Tragfähigkeitsnachweis – Grundlagen

Der wichtigste Werkstoffkennwert ist die Zugfestigkeit. Der Nachweis der Tragfähigkeit erfolgt über zwei Grenzzustände:

Grenzzustand der Tragfähigkeit: Der Grenzzustand der Schraube, dessen Überschreiten zu einem rechnerischen Versagen führt.

Grenzzustand der Gebrauchstauglichkeit: Der Grenzzustand der Schraube, dessen Überschreiten die Nutzung unter festgelegten Bedingungen nicht mehr gewährleistet.

Merke dir! Biegebeanspruchungen sollten auf jedem Fall in einer Schraubenverbindung vermieden werden.

Auswahl des passenden Werkstoffs für die Schraube

Da eine Schraubenverbindung, also Schraube mit Gewinde und Gegengewinde, zumeist höheren Belastungen ausgesetzt ist, empfiehlt es sich im Vorfeld den richtigen Werkstoff auszusuchen. Als Entscheidungshilfe dienen uns die bisher bestimmten oder aufgeführten Größen wie:

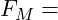$F_M =$ Montagekraft
$F_A =$ Betriebskraft
$F_M + F_A = F_S$ Schraubengesamtkraft

So ist es auch die Schraubengesamtkraft, die wir bei der Werkstoffauswahl als entscheidende Größe berücksichtigen sollten, denn nun wenn dieser Kraft durch den richtigen Werkstoff ertragen werden kann, hält die Schraube.

Der Schraubenwerkstoff selber sollte eine besonders hohe Festigkeit und eine ausreichende Plastizität (Zähigkeit) aufweisen. Die Plastizität ist wichtig, da reine hochfeste Werkstoffe eine besonders hohe Kerbempfindlichkeit aufweisen.

Die passende Wahl von Festigkeit und Zähigkeit als Kombination, lässt sich nur als Kompromiss bewerkstelligen.

Festigkeitswerte des Schraubenwerkstoffs

Wie in vielen anderen Bereichen des Maschinenbaus und der Montagetechnik wählen wir Größen aus dem Spannungs-Dehnungs-Diagramm um den Werkstoff genau beurteilen zu können. Uns helfen die Größen:

$R_{eH} =$ Streckgrenze
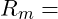$R_m =$ Zugfestigkeit

Beide Werkstoffkennwerte findest du in den zumeist auf dem Schraubenkopf, sofern es sich um einen Sechskantschraubenkopf handelt.

Werkstoffangaben auf der Schraube

Nähere Informationen zur Kennzeichnung erhältst du in der DIN EN 20898 und der DIN EN 493!

Unabhängig vom Ausgangsmaterial werden $R_{eH}$ und $R_m$ durch zwei durch einen Punkt getrennte Kennziffern ausgedrückt.

Beispiel mit der Angabe $10.9$ .

Es handelt sich hierbei um eine vergleichsweise kritische Schraube.
Die hintere Ziffer 9 wird mit der vorderen Ziffer 10 und dem Faktor 10 multipliziert: $9 \cdot 10 \cdot 10 = 900 \frac{N}{mm^2} = R_{eH}$
Die vordere Ziffer 10 wird mit dem Faktor 100 multipliziert: $10 \cdot 100 = 1000 \frac{N}{mm^2} = R_m$

Tragfähigkeitsnachweis – Bestimmung der Vergleichsspannung

Im ersten Schritt müssen wir für den Tragfähigkeitsnachweis die Vergleichsspannung $\sigma_v$ der Schraubenverbindung ermitteln. Die Bestimmung erfolgt mit Hilfe der Gestaltänderungsenergiehypothese, kurz GEH.

In den meisten Fällen tritt ein zweiachsiger Spannungszustand auf, der sowohl eine Zugbeanspruchung $\sigma_z$ als auch eine Torsionsbeanspruchung $\tau$ beinhaltet.

Die Zugbeanspruchung tritt infolge der Montagevorspannung auf und ermittelt sich durch:

$\sigma_z = \frac{F_M}{A_S}$

wobei

$A_S = \frac{\pi}{4} \cdot (\frac{d_2 + d_3}{2})^2$

Kennzahlen:

$\sigma_z =$ Zugspannung

$F_M =$ Montagekraft

$A_S =$ Querschnittsfläche (Spannungsquerschnitt)

$(\frac{d_2 + d_3}{2})^2 = d_s$ [ $d_s$ ist kleiner als Schaftdurchmesser $d_T$ ]

Die Torsionsbeanspruchung tritt infolge des Reibmomentes im Gewinde auf und ermittelt sich durch:

$\tau = \frac{M_G}{W_p}$

wobei

$W_p = \frac{\pi}{16} d_s^3$

Kennzahlen:

$\tau =$ Torsionsspannung

$M_G =$ Reibmoment

$W_p =$ polares Widerstandsmoment

$(\frac{d_2 + d_3}{2})^2 = d_S$ [ $d_S$ ist kleiner als Schaftdurchmesser $d_T$ ]

Die Gleichung für die Vergleichsspannung berücksichtigt diese beiden Größen.

$\sigma_v = \sqrt{ \sigma_z^2 + 3 \tau^2}$

Kennzahlen:

$\sigma_v =$ Vergleichsspannung

$\sigma_z =$ Zugbeanspruchung

$\tau =$ Torsionsbeanspruchung

Haben wir die beiden Werte gegeben und errechnen daraus die Vergleichsspannung mit der obigen Gleichung, so ist es uns anschließend möglich, diese mit den Herstellerangaben (Schraubenwerkstoffkennwerten) zu vergleichen. Ist die Vergleichsspannung niedriger oder gleich der Herstellerangaben, so ist davon auszugehen, dass die Schraubenverbindung den einwirkenden Belastungen standhält. Liegt sie jedoch oberhalb der Herstellerangaben so ist mit einem Versagen der Schraubenverbindung zu rechnen:

$\sigma_v \ge \frac{R_{eH}}{\nu}$ Schraubenverbindung hält.

$\sigma_v > \frac{R_{eH}}{\nu}$ Schraubenverbindung versagt.

Kennzahlen:

$\sigma_v =$ Vergleichsspannung

$R_{eH} =$ Obere Streckgrenze

$\nu =$ Sicherheit (Faktor variiert je nach Belastungsart [statisch oder dynamisch])

Liegt eine statische Belastung vor, so wird die Sicherheit mit einem Faktor von $\nu = 1,1 - 1,3$ angenommen.

Liegt eine dynamische Belastung vor, so wird die Sicherheit mit einem Faktor von $\nu = 1,5 - 1,8$ angenommen.

Sofern eine Betriebskraft ebenfalls berücksichtigt werden soll, so kann ihr statischer Anteil der Montagekraft hinzuaddiert werden, womit wir die Angabe der Vergleichspannung haben.

Auf der anderen Seite kann auch der dynamische Anteil der Betriebskraft als Ausschlagspannung berücksichtigt werden.

Tragfähigkeitsnachweis – Flächenpressung

Als nächste wichtige Größe bestimmen wir die Flächenpressung. Die Flächenpressung tritt bei einer Schraubenverbindung durch Vorspannkräfte und Betriebskräften auf, soll aber nach Möglichkeit weitestgehend vermieden werden. Der Grund für diese Vermeidungshaltung liegt im dadurch bedingten Auftreten von Kriechvorgängen. Letztere sorgen dann wieder für Vorspannungsverluste.

Durchsteckschraube

Handelt es sich um eine Durchsteckschraubenverbindung so tritt die Flächenpressung zwischen dem Schraubenkopf und den verspannten Teilen sowie auf der gegenüberliegenden Seite zwischen verspannten Teilen und Mutter auf.

Sacklochschraube

Bei einer Sacklochschraubenverbindung beschränkt sich die Flächenpressung hingegen lediglich auf den Bereich zwischen Schraubenkopf und verspannten Teilen.

Grenzflächenpressung

Unabhängig von der Wahl der Schraubenverbindung nimmt man als Grenzwert für die Flächenpressung die Grenzflächenpressung $p_{zul}$ an. Dieser Wert variiert je nach ausgewähltem Schraubenwerkstoff. Bleibt der Wert für die Flächenpressung unterhalt dieses Grenzwert, so kann davon ausgegangen werden, dass Kriechvorgänge ausbleiben.

Die nächste Übersicht zeigt einige Werkstoffangaben zur Grenzflächenpressung im Zusammenhang mit der Mittelspannung $R_M$ .

Tragfähigkeitsnachweis – Schraubenwerkstoffe – Übersicht

Berechnung der Flächenpressung

Bevor wir nun mit der Berechnung starten, schauen wir uns mal genau an, wo und wie die Flächenpressung im Bereich zwischen Kopf der Schraube und verspannten Teilen auftritt.

SKIZZE

Wie du siehst, wirkt die Flächenpressung ringförmig zwischen Kopf und Verspannteilen. In der nachfolgenden Berechnung benutzen wir die Ringfläche

$A_P = \frac{\pi}{4} \cdot (d_w^2 - d_a^2)$

Mit dieser Größe können wir nun die (Un-)Gleichung für die Flächenpressung aufstellen. Diese errechnet sich wie folgt:

$p_{zul} \le \frac{F_S}{A_P}$

eingesetzt:

$p_{zul} \le \frac{F_S}{\frac{\pi}{4} \cdot (d_w^2 - d_a^2)}$

Wie geht es weiter?...

Nachdem wir jetzt wissen, welche Berechnungen uns im Betriebszustand einer Schraubenverbindung begegnen können, führen wir im nächsten Schritt den Tragfähigkeitsnachweis durch.

Was gibt es noch bei uns?

Finde die richtige Schule für dich!

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe.de?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Interaktive Übungsaufgaben

Demo–Quizfrage 1

Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?

Auszüge aus unserem Kursangebot

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
ET1 (Grundlagen der Elektrotechnik) und
ET2 (Gleichstromtechnik) an.

Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++