
Unterschied zwischen Betriebszustand & Montagezustand
Der Betriebszustand einer Schraubenverbindung liegt vor, wenn eine im Montagezustand befindliche Schraubenverbindung durch zusätzliche Kräfte (Betriebskräfte) belastet wird.
Die Betriebskräfte ![]() (A = Axial) kennzeichnet, dass sie axial zur Schraubenachse auf die Verbindung einwirken.
(A = Axial) kennzeichnet, dass sie axial zur Schraubenachse auf die Verbindung einwirken.
Die Kräfte bewirken sowohl eine Längung der Schraube als auch eine Stauchung der verspannten Teile.
Für eine besseres Verständnis schauen wir uns zunächst den Vergleich zwischen dem Montagezustand und dem Betriebszustand wie in der nachfolgenden Abbildung dargestellt genauer an.
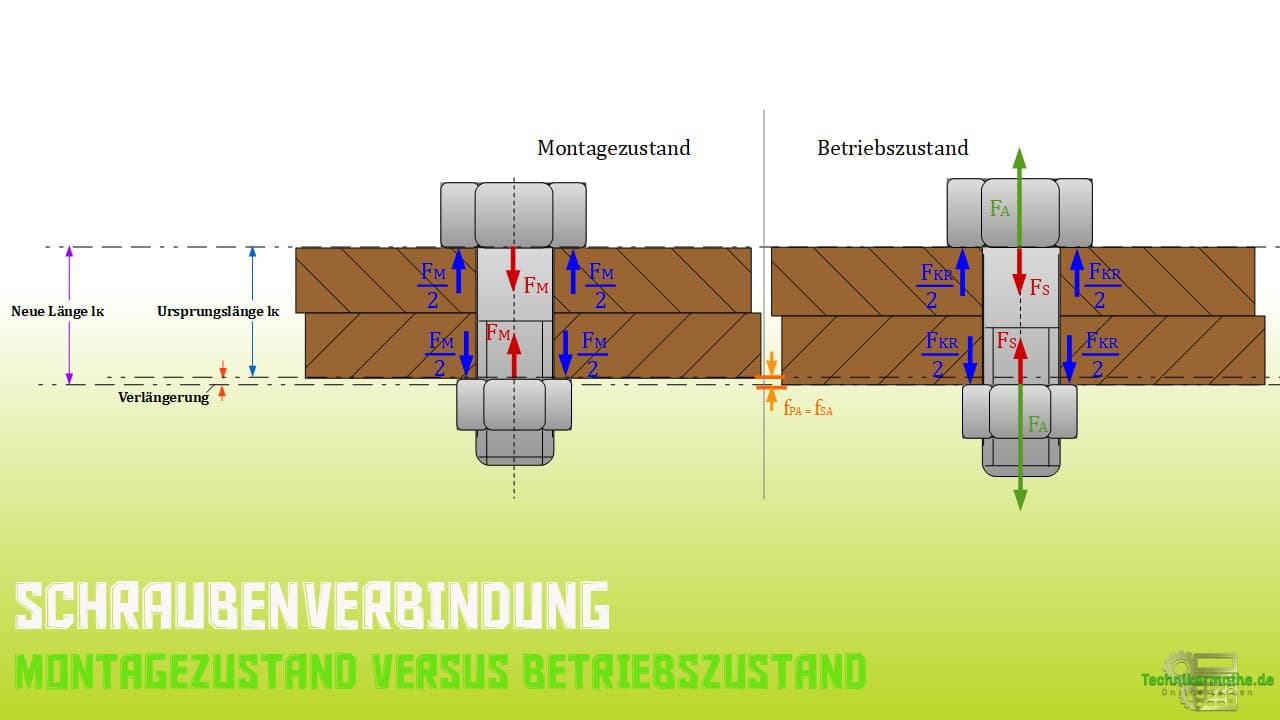
Es zeigt sich, dass nun mit den Betriebskräften andere Kräfte zusätzlich zum Tragen kommen.
Die Betriebskraft ![]() bewirkt dabei eine Längung der Schraube um den Anteil
bewirkt dabei eine Längung der Schraube um den Anteil ![]() und eine Stauchung der verspannten Teile um den Anteil
und eine Stauchung der verspannten Teile um den Anteil ![]() .
.
Da es sich um eine feste Verbindung zwischen Schraube und verspannten Teilen handelt, müssen beide Anteile von ![]() und
und ![]() betragsmäßig identisch sein.
betragsmäßig identisch sein.
![]()
Sowie
![]()
Kennzahlen:
![]() Längenänderung
Längenänderung
![]() Längung der Schraube
Längung der Schraube
![]() Stauchung der verspannten Teile
Stauchung der verspannten Teile
![]() Betragsstriche
Betragsstriche
Vergleich der Kraftverhältnisse zwischen Montagezustand und Betriebszustand
Die Betriebskraft ![]() sorgt für eine Änderung innerhalb des Kräftegleichgewichts sowohl von der Schraube (mit
sorgt für eine Änderung innerhalb des Kräftegleichgewichts sowohl von der Schraube (mit ![]() ) als auch der verspannten Teile (mit
) als auch der verspannten Teile (mit ![]() ).
).
Das Kräftegleichgewicht der Schraube können wir über die Schraubenkraft abbilden.
Im Montagezustand entspricht die Schraubenkraft der Montagekraft:
![]()
Kennzahlen:
![]() = Schraubenkraft
= Schraubenkraft
![]() = Montagekraft
= Montagekraft
Im Betriebszustand wird die Schraubenkraft neben der Montagekraft zusätzlich um die Betriebskraft verstärkt, weshalb letztere positiv in die Berechnung eingeht.
![]()
Kennzahlen:
![]() = Schraubenkraft
= Schraubenkraft
![]() = Montagekraft
= Montagekraft
![]() = Anteil der Betriebskraft der Schraube
= Anteil der Betriebskraft der Schraube
Das Kräftegleichgewicht der verspannten Teile können wir über die Klemmkraft abbilden.
Im Montagezustand entspricht die Schraubenkraft der Montagekraft:
![]()
Kennzahlen:
![]() = Klemmkraft
= Klemmkraft
![]() = Montagekraft
= Montagekraft
Im Betriebszustand wird die Klemmkraft neben der Montagekraft zusätzlich um die Betriebskraft reduziert, weshalb letztere negativ in die Berechnung eingeht.
![]()
Kennzahlen:
![]() = Klemmkraft
= Klemmkraft
![]() = Montagekraft
= Montagekraft
![]() = Anteil der Betriebskraft der verspannten Teile.
= Anteil der Betriebskraft der verspannten Teile.
Verspannungsschaubild für den Betriebszustand.
Wir haben uns ja bereits ausführlich mit dem Verspannungsschaubild für den Montagezustand befasst und dieses auch für unterschiedliche Montagezustände mit verschiedenen Montagekräften erstellt.
Daraus konnten wir Rückschlüsse hinsichtlich der Längenänderungen von Schraube und Verspannteilen ziehen.
Zur Erinnerung nachfolgende das Verspannungsschaubild für den Montagezustand.
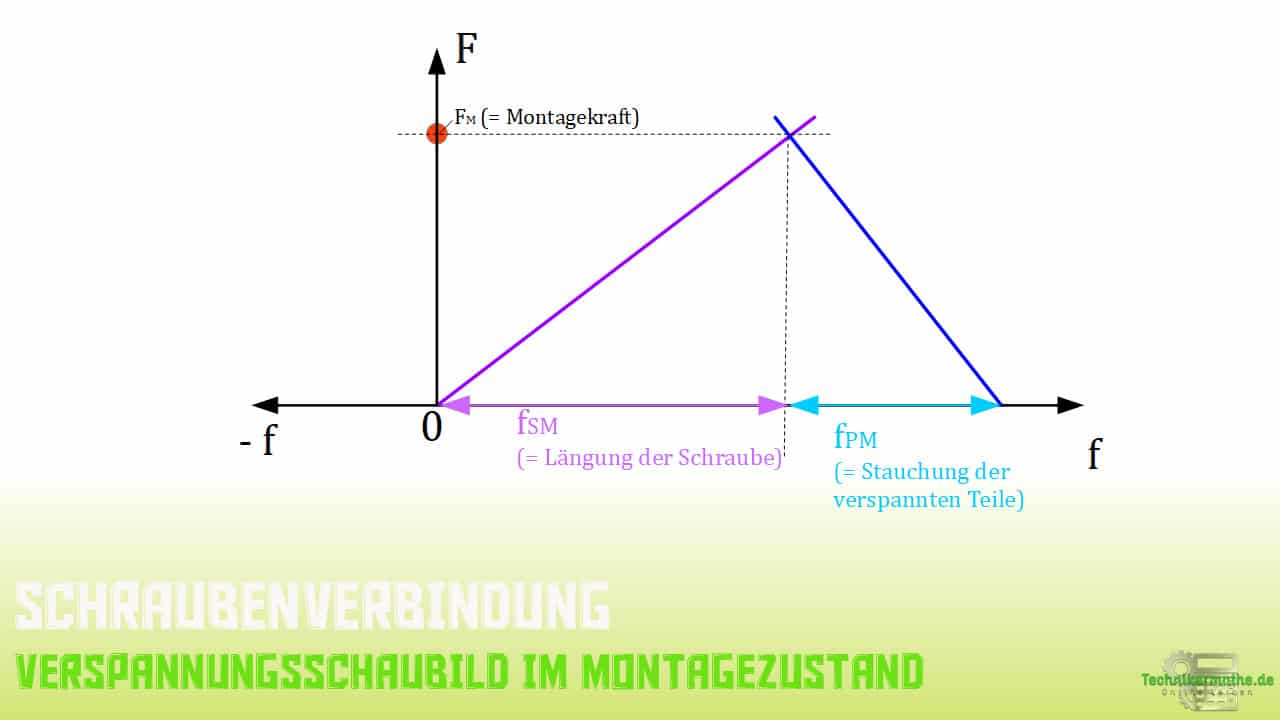
Die drei eingezeichneten Größen
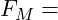 Montagekraft
Montagekraft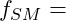 Längenänderung der Schraube (Längung)
Längenänderung der Schraube (Längung)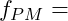 Längenänderung der Verspannteile (Stauchung)
Längenänderung der Verspannteile (Stauchung)
sollten dir bereits geläufig sein.
Mit der Betriebskraft ![]() tragen wir nun eine zusätzliche Kraft anteilig über und unterhalb der Montagekraft
tragen wir nun eine zusätzliche Kraft anteilig über und unterhalb der Montagekraft ![]() auf der Y-Achse auf, wodurch es folgerichtig zu einer Änderung von
auf der Y-Achse auf, wodurch es folgerichtig zu einer Änderung von ![]() und
und ![]() kommt, die zuvor noch deckungsgleich mit
kommt, die zuvor noch deckungsgleich mit ![]() waren.
waren.
Die Zusatzbelastung (Anteil der Betriebskraft) der Schraube ![]() sorgt für eine Erhöhung der Gesamtschraubenkraft:
sorgt für eine Erhöhung der Gesamtschraubenkraft:
![]()
Die Minderbelastung (Anteil der Betriebskraft) der Verspannteile ![]() sorgt für eine Senkung der Gesamtklemmkraft:
sorgt für eine Senkung der Gesamtklemmkraft:
![]()
![]()
Im Verspannungsschaubild tragen wir ![]() nach oben ab, wodurch sich ein neuer Punkt auf der Geraden ergibt (grün).
nach oben ab, wodurch sich ein neuer Punkt auf der Geraden ergibt (grün).
![]() hingegen tragen wir nach unten ab, wodurch sich auch hier ein neuer Punkt auf der Gerade ergibt (grün)
hingegen tragen wir nach unten ab, wodurch sich auch hier ein neuer Punkt auf der Gerade ergibt (grün)
Nun ziehen wir jeweils eine horizontale Gerade von den Punkten zu der Y-Achse und haben dann unsere neuen Werte für ![]() und
und ![]() .
.
Die neue Angabe von ![]() zeigt uns welche Kräfte die Schraube aus materieller Sicht aushalten muss, ohne zu brechen.
zeigt uns welche Kräfte die Schraube aus materieller Sicht aushalten muss, ohne zu brechen.
- Daher sollte sich die Werkstoffauswahl für die Schraube immer an der Schraubenkraft im Betriebszustand orientieren und nicht fälschlicherweise im Montagezustand.
- Ebenfalls sollte bei der Verbindung darauf geachtet werden, dass die Klemmkraft im Betriebszustand geringer ausfällt als im Montagezustand. Sorgen die Betriebskräfte dafür, dass die Klemmkraft den Wert 0 annimmt, so ist die Verbindung nicht mehr gegeben.
Kraftverhältnis im Betriebszustand
Das Kraftverhältnis ![]() im Betriebszustand berücksichtigt die Schraubenzusatzkraft
im Betriebszustand berücksichtigt die Schraubenzusatzkraft ![]() und die Zusatzkraft der verspannten Teile
und die Zusatzkraft der verspannten Teile ![]() als einen Anteil der axial wirkenden Kraftkomponente der Betriebskraft
als einen Anteil der axial wirkenden Kraftkomponente der Betriebskraft ![]() .
.
Daher ist es nur sinnig das Kraftverhältnis in die bisherigen Gleichungen zur Schraubenzusatzkraft und der Zusatzkraft der verspannten Teile zu übernehmen.
Bis wir jedoch bei diesen Gleichungen ankommen, müssen wir zuvor noch ein paar Schritte berücksichtigen. Die Vorgehensweise erfolgt dabei schrittweise:
Schritt 1 – Zusatzkraft
Im ersten Schritt stellen wir ausgehend von der Gleichung für die Nachgiebigkeit durch Auflösen nach ![]() die beiden Gleichungen auf:
die beiden Gleichungen auf:
Ausgangsgleichung: 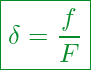
Kennzahlen:
![]() Elastische Nachgiebigkeit
Elastische Nachgiebigkeit
![]() Längenänderung
Längenänderung
![]() Kraft
Kraft
Umgestellt: ![]()
Angepasst für die Schraubenzusatzkraft im Betriebszustand
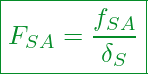
Kennzahlen:
![]() Elastische Nachgiebigkeit der Schraube
Elastische Nachgiebigkeit der Schraube
![]() Längenänderung der Schraube
Längenänderung der Schraube
![]() Schraubenzusatzkraft
Schraubenzusatzkraft
Angepasst für die Zusatzkraft der verspannten Teile im Betriebszustand
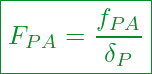
Kennzahlen:
![]() Elastische Nachgiebigkeit der verspannten Teile
Elastische Nachgiebigkeit der verspannten Teile
![]() Längenänderung der verspannten Teile
Längenänderung der verspannten Teile
![]() Zusatzkraft der verspannten Teile
Zusatzkraft der verspannten Teile
Schritt 2 – Elastische Nachgiebigkeit
Da wir bereits wissen, dass die Längenänderungen von verspannten Teilen und Schrauben im Betriebszustand betragsmäßig identisch sind mit
![]() , und es gilt
, und es gilt
![]() sowie
sowie
![]()
können wir im nächsten Schritt durch Gleichsetzen eine Gleichung aufstellen, die dies berücksichtigt:
![]()
oder
![]()
Kennzahlen:
![]() Elastische Nachgiebigkeit der Schraube
Elastische Nachgiebigkeit der Schraube
![]() Schraubenzusatzkraft
Schraubenzusatzkraft
![]() Elastische Nachgiebigkeit der verspannten Teile
Elastische Nachgiebigkeit der verspannten Teile
![]() Zusatzkraft der verspannten Teile
Zusatzkraft der verspannten Teile
Schritt 3 – Herleiten der Gleichung für die Schraubenzusatzkraft
Aus den bisherigen Gleichungen wissen wir ebenfalls, dass
![]()
Ist. Für das weitere Vorgehen lösen wir diese Gleichung nach ![]() auf:
auf:
![]()
Im nächsten Schritt setzen wir diese Gleichung in die Gleichung ![]() ein und erhalten:
ein und erhalten:
![]()
Nun multiplizieren wir die Klammer aus:
![]()
Das Ausklammern von ![]() führt zu nachfolgender Gleichung:
führt zu nachfolgender Gleichung:
![]()
Die finale Gleichung für die Schraubenzusatzkraft erhalten wir, wenn wir die bisherige Gleichung nach ![]() auflösen:
auflösen:
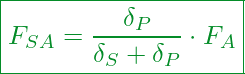
Schritt 4 – Herleiten der Gleichung für die Zusatzkraft der verspannten Teile:
Aus den bisherigen Gleichungen wissen wir ebenfalls, dass
![]()
Ist. Für das weitere Vorgehen lösen wir diese Gleichung nach ![]() auf:
auf:
![]()
Im nächsten Schritt setzen wir diese Gleichung in die Gleichung ![]() ein und erhalten:
ein und erhalten:
![]()
Nun multiplizieren wir die Klammer aus:
![]()
Das Ausklammern von ![]() führt zu nachfolgender Gleichung:
führt zu nachfolgender Gleichung:
![]()
Die finale Gleichung für die Schraubenzusatzkraft erhalten wir, wenn wir die bisherige Gleichung nach ![]() auflösen:
auflösen:
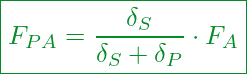
Nun haben wir zwei Gleichungen mit deren Hilfe wir unter Kenntnis der Betriebskraft ![]() und den jeweiligen Nachgiebigkeiten
und den jeweiligen Nachgiebigkeiten ![]() sowie
sowie ![]() die beiden Zusatzkräfte berechnen können.
die beiden Zusatzkräfte berechnen können.
Schritt 5 – Bestimmung der Kraft mit Kenntnis von Betriebskraft und Kraftverhältnis
Das Kraftverhältnis ![]() ergibt sich in unserem Fall aus dem Quotienten von Schraubenzusatzkraft
ergibt sich in unserem Fall aus dem Quotienten von Schraubenzusatzkraft ![]() und axialer Betriebskraft
und axialer Betriebskraft ![]() .
.
Da wir annehmen, dass die Krafteinleitung über den Schraubenkopf erfolgt, erhält ![]() einen Index
einen Index ![]() und wird zu
und wird zu ![]() .
.
Wird die Kraft an anderer Stelle eingeleitet, so wählen wir einen anderen Index.
Als Gleichung für das Kraftverhältnis erhalten wir:
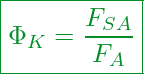
Kommt dir die rechte Seite der Gleichung vielleicht bekannt vor? Bestimmt! Denn unsere obige Gleichung für die Schraubenzusatzkraft können wir ebenfalls umstellen:
![]()
Wenn wir jetzt die beiden Gleichungen gleichsetzen, schaffen wir eine neue Gleichung, bei der sich das Kraftverhältnis mit Hilfe der Nachgiebigkeiten ![]() und
und ![]() errechnet.
errechnet.
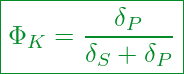
Schritt 6 – Vereinfachung der Gleichungen für die Zusatzkräfte
Ausgehend von der letzten Gleichung können wir die beiden Gleichungen für die Zusatzkräfte umformulieren
- Aus
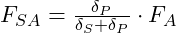 wird
wird
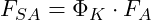
- Und aus
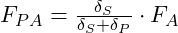 wird
wird
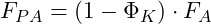
![]()
Ersetzen wir nun die 1 auf der rechten Seite der Gleichungen durch einen gleichwertigen Bruch, so erhalten wir:
![]()
Diese Gleichung lässt sich alternativ wie folgt schreiben:
![]()
Dies entspricht dann:
![]()
Gesamtbelastung der Schraubenverbindung
Nachfolgend führen wir unsere Berechnung für das Vorliegen einer statisch und anschließend dynamisch wirkenden Betriebskraft durch.
Gesamtbelastung der Schraubenverbindung bei statischer Betriebslast
Dabei helfen uns die nachfolgenden drei Erkenntnisse weiter:
- Befindet sich die Schraubenverbindung im Betriebszustand so treten mit
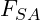 und
und 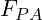 zwei zusätzliche Kräfte (jeweils anteilig) auf.
zwei zusätzliche Kräfte (jeweils anteilig) auf.
- Wir wissen ebenfalls, dass in Berechnungen zum Betriebszustand diese Anteile bei der Auslegung berücksichtigt werden müssen, damit es weder zum Schraubenbruch noch zum Klemmkraftverlust der Verbindung kommt.
- Unter Kenntnis der Betriebskraft und der beiden Nachgiebigkeiten lassen sich
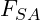 und
und 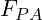 einfach berechnen.
einfach berechnen.
Gesamtbelastung der Schraube
Die Gleichung ist folgende:
![]()
Angepasst erhalten wir für die Schraubengesamtkraft eine Gleichung, die sich aus der Summe von Montagekraft ![]() und anteiliger Betriebskraft (
und anteiliger Betriebskraft (![]() ) zusammensetzt.
) zusammensetzt.
![]()
Kennzahlen
![]() Schraubengesamtkraft (Belastung)
Schraubengesamtkraft (Belastung)
![]() Montagekraft
Montagekraft
![]() Kraftverhältnis
Kraftverhältnis
![]() Betriebskraft (statisch)
Betriebskraft (statisch)
Gesamtbelastung der verspannten Teile
Die Gleichung ist folgende:
![]()
Angepasst erhalten wir für die Gesamtkraft der verspannten eine Gleichung, die sich aus der Differenz von Montagekraft ![]() und anteiliger Betriebskraft (
und anteiliger Betriebskraft (![]() ) zusammensetzt.
) zusammensetzt.
![]()
Kennzahlen
![]() Gesamtkraft (Belastung) der verspannten Teile
Gesamtkraft (Belastung) der verspannten Teile
![]() Montagekraft
Montagekraft
![]() Kraftverhältnis
Kraftverhältnis
![]() Betriebskraft (statisch)
Betriebskraft (statisch)
Gesamtbelastung der Schraubenverbindung bei dynamischen Betriebslast
Anders als im statischen Betriebszustand mit einer konstanten Belastung, variiert die dynamische Betriebskraft hinsichtlich der Belastungshöhe.
Um dennoch eine einigermaßen überschaubare Gleichung ermitteln zu können, bilden wir sowohl für die Schraube als auch die verspannten Teile Mittelwerte von den Belastungen.
Da dieses Thema sehr tief in den Maschinenbau eindringt, begnügen wir uns mit der Gleichung für eine sinusförmige Belastung durch die Betriebskraft.
So errechnet sich die Schraubenzusatzkraft mit:
![]()
Die mittlere Schraubenkraft ![]() ist dann zu berechnen mit:
ist dann zu berechnen mit:
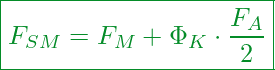
Krafteinleitungskennzahl
Die Krafteinleitungskennzahl oder auch Krafteinleitungsfaktor ![]() genannt, wird aus der gedachten Angriffsposition der Betriebskraft ermittelt und bestimmt so das Kraftverhältnis linear.
genannt, wird aus der gedachten Angriffsposition der Betriebskraft ermittelt und bestimmt so das Kraftverhältnis linear.
Formal errechnet sich dieser Faktor aus dem Quotienten von tatsächlicher Klemmlänge ![]() und konstruktiver Klemmlänge
und konstruktiver Klemmlänge ![]()
![]()
Wobei gilt
![]()
Nimmt der Krafteinleitungsfaktor den Wert ![]() an, so wirkt die axiale Betriebskraft über die gesamte Schaftlänge und die anteilige Gewindelänge, welche die Schraube zusätzlich belastet und die verspannten Teile entlastet. Tatsächliche Klemmlänge und konstruktive Klemmlänge sind dabei gleich groß.
an, so wirkt die axiale Betriebskraft über die gesamte Schaftlänge und die anteilige Gewindelänge, welche die Schraube zusätzlich belastet und die verspannten Teile entlastet. Tatsächliche Klemmlänge und konstruktive Klemmlänge sind dabei gleich groß.
In der nächsten Abbildung sind diese Größen nochmals aufgeführt:
SKIZZE
Anders verhält sich dies, wenn die Betriebskraft seitlich von der Schraubenverbindung eingeleitet wird. Hier greift die Betriebskraft an den verspannten Teilen an.
SKIZZE
Durch das seitliche Angreifen, erhalten wir für den Krafteinleitungsfaktor einen Wert von ![]() . Ein Teil der verspannten Teile wird also gestaucht und der andere Teil entlastet.
. Ein Teil der verspannten Teile wird also gestaucht und der andere Teil entlastet.
In Bezug auf unser Kraftverhältnis ergänzen wir ![]() einfach als Faktor in der Gleichung:
einfach als Faktor in der Gleichung:
So wird aus:
![]() (Montagezustand)
(Montagezustand)
Jetzt
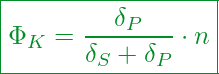 (Betriebszustand)
(Betriebszustand)
Gleiches gilt für die bisherige Nachgiebigkeitsberechnung der Schraube und der verspannten Teile:
Schraube:
![]() (Montagezustand)
(Montagezustand)
Jetzt:
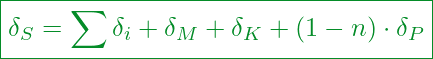 (Betriebszustand)
(Betriebszustand)
Verspannte Teile:
![]() (Montagezustand)
(Montagezustand)
Jetzt:
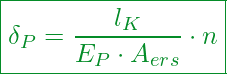 (Betriebszustand)
(Betriebszustand)
Setzkraftverluste
Ein Setzen liegt immer dann vor, wenn sich bei der Schraube und den verspannten Teilen eine plastische Verformung, bzw. plastische Längenänderung, aufgrund von Krafteinwirkungen einstellt.
Diese Längenänderung ist bleibend. Da plastische Verformungen eigentlich immer unerwünscht sind, muss eine elastische Vorspannung der Schraubenverbindung eingestellt werden, die das Setzen vollständig kompensiert.
Der Hauptbereich der plastischen Verformung liegt jeweils an der Oberfläche von Schraube und verspannten Teilen. Hier wird die raue Oberfläche mit ihren Unebenheiten durch das Anziehen der Schraube plattgedrückt, wodurch es zu einer minimalen Entlastung der Verbindungselemente kommt. Dies führt dann wieder zu einem Lockern der Verbindung, welches der Techniker als Setzkraftverlust bezeichnet.
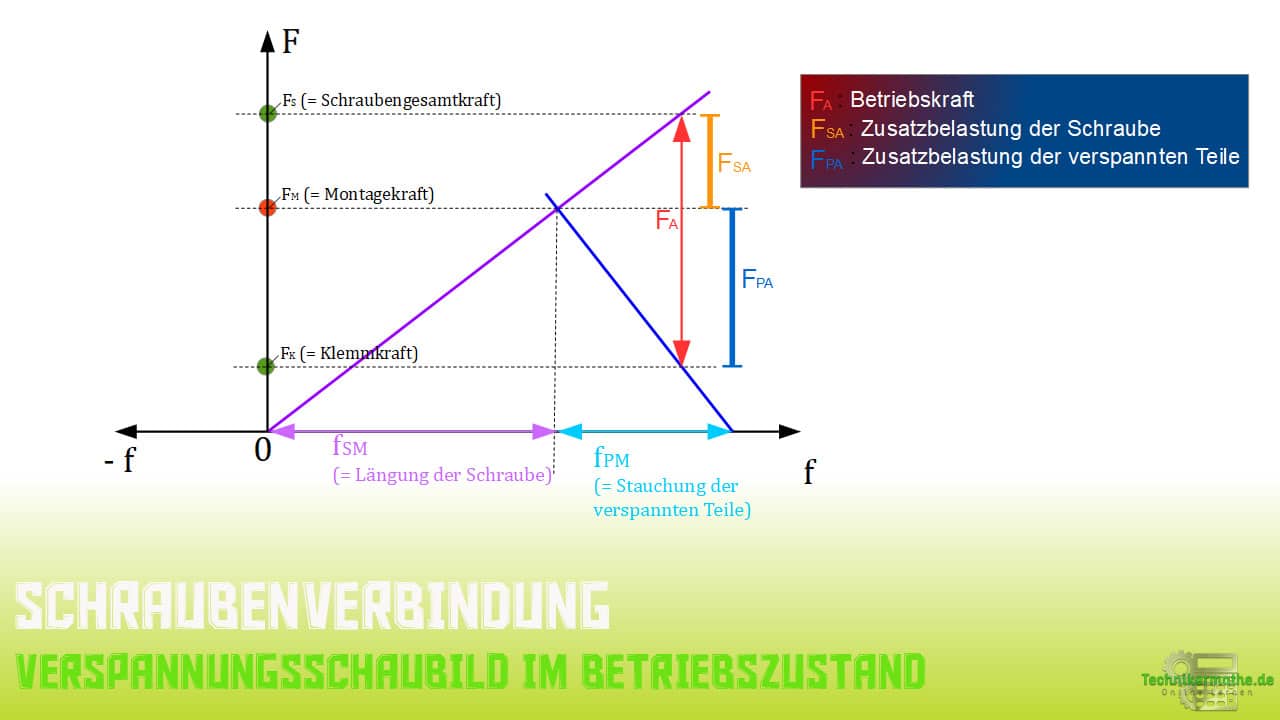
Dieser Verlust lässt sich auf rechnerischem Wege durch den Setzbetrag ![]() bestimmen. Formal sieht das dann wie folgt aus:
bestimmen. Formal sieht das dann wie folgt aus:
![]()
Kennzahlen
![]() Setzbetrag
Setzbetrag
![]() Anteil des Setzens der Schraube
Anteil des Setzens der Schraube
![]() Anteil des Setzens der verspannten Teile
Anteil des Setzens der verspannten Teile
In der nächsten Abbildung siehst du noch mal, wie sich der Setzbetrag auf die Gerade im Verspannungsschaubild auswirkt.
SKIZZE
So sorgt der Setzbetrag ![]() dafür, dass die Gerade nach links verschoben wird und sich dadurch ein neuer Schnittpunkt mit einer gleichzeitig geringeren Montagekraft einstellt. Den Betrag, um welchen die Montagekraft abnimmt, bezeichnen wir als Setzkraftverlust
dafür, dass die Gerade nach links verschoben wird und sich dadurch ein neuer Schnittpunkt mit einer gleichzeitig geringeren Montagekraft einstellt. Den Betrag, um welchen die Montagekraft abnimmt, bezeichnen wir als Setzkraftverlust ![]() .
.
Dass Setzkraftverluste uns sogar regelmäßig im Alltag begegnen, zeigt sich beispielsweise beim jährlichen Reifenwechsel. Hier empfiehlt uns der Reifen-/Fahrzeughersteller, die Radmuttern an den Felgen nach einem Reifenwechsel nachzuziehen. Empfohlen wird dies nach einer Strecke von 50 gefahrenen Kilometern.
Maßnahmen um Setzkraftverluste auszugleichen
In der Montagetechnik sieht man von einem Nachziehen ab und wählt daher konstruktive Maßnahmen, die einen Setzkraftverlust ausgleichen und somit eine Nachbehandlung überflüssig machen.
Maßnahmen, die sich hierbei bewährt haben, sind:
- Unter den Schraubenkopf wird eine federnde Unterlegscheibe gelegt – plastische Verformung nur bei der Unterlegscheibe.
- Der Schraubenkopf wird mit einem federnden Bereich konstruiert – gleicher Effekt wie bei der Unterlegscheibe.
- Einsatz längerer Schrauben – Dies erhöht die Klemmlänge
- Einsatz hochfester Schrauben – Diese erhöht ebenfalls die Klemmlänge, begünstigt aber zeitgleich die Kerbempfindlichkeit.
Was gibt es noch bei uns?
Was ist Technikermathe.de?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Interaktive Übungsaufgaben

Demo–Quizfrage 1
Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?
Auszüge aus unserem Kursangebot
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
ET1 (Grundlagen der Elektrotechnik) und
ET2 (Gleichstromtechnik) an.
Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++
Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++
Technikermathe.de meets Social-Media
Dein Technikermathe.de-Team








