Schraubenverbindung Teil 2 – Montagezustand

Montagezustand und Betriebszustand

Nachdem wir uns ausgiebig mit den Nachgiebigkeiten von Schrauben und verschrauben Teilen befasst haben, werden wir uns nun die Schraubenverbindung im Montagezustand und anschließend im Betriebszustand betrachten. Dabei bestimmen wir für beide Zustände die Kraftverhältnisse und die Verformungsverhältnisse.

Montage

Nachdem wir alle zu verschraubenden Bauteile ordentlich ausgelegt haben, werden diese jetzt montiert. Durch das Anziehen der Schrauben erfolgt eine Stauchung der zu verspannenden Teile und im Umkehrschluss eine Dehnung (Längung) der Schraube.

Verursacht wird dieser Zustand der Stauchung und Dehnung durch die Montagekraft $F_M$ .

Da wir uns noch immer im Zustand der Montage befinden, treten keine zusätzlichen Kräfte in Form von Betriebskräften auf.

Welche Kräfte zum jetzigen Zeitpunkt auf die Schraube und die verspannten Teile jeweils einwirken, schauen wir uns in den beiden folgenden Grafiken näher an.

Schraube im Montagezustand

Auf der linken Bildseite siehst du die Darstellung der Schraube im unbelasteten und auf der rechten Bildseite die Darstellung der Schraube im gedehnten (montierten) Zustand.

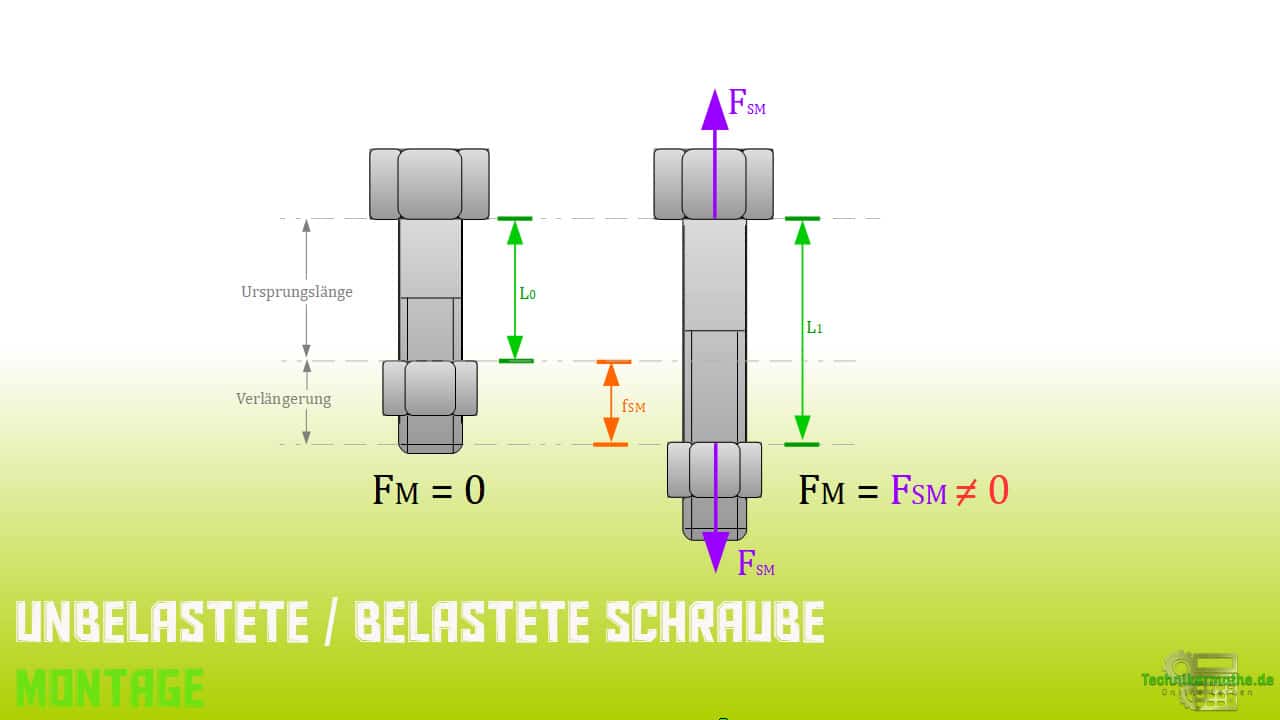
Montagezustand - Unbelastete und belastete Schraube — Montagezustand – Unbelastete und belastete Schraube

Neben der Montagekraft der Schraube $F_{SM}$ [S = Schraube], können wir als zweite Größe die Längenänderung der Schraube $f_{SM}$ aus der Grafik ablesen.

Verspannte Teile im Montagezustand

Auch hier sehen wir auf der linken Bildseite die Darstellung der zu verspannenden Teile im unbelasteten und auf der rechten Bildseite die Darstellung der verspannten Teile im gestauchten (montierten) Zustand.

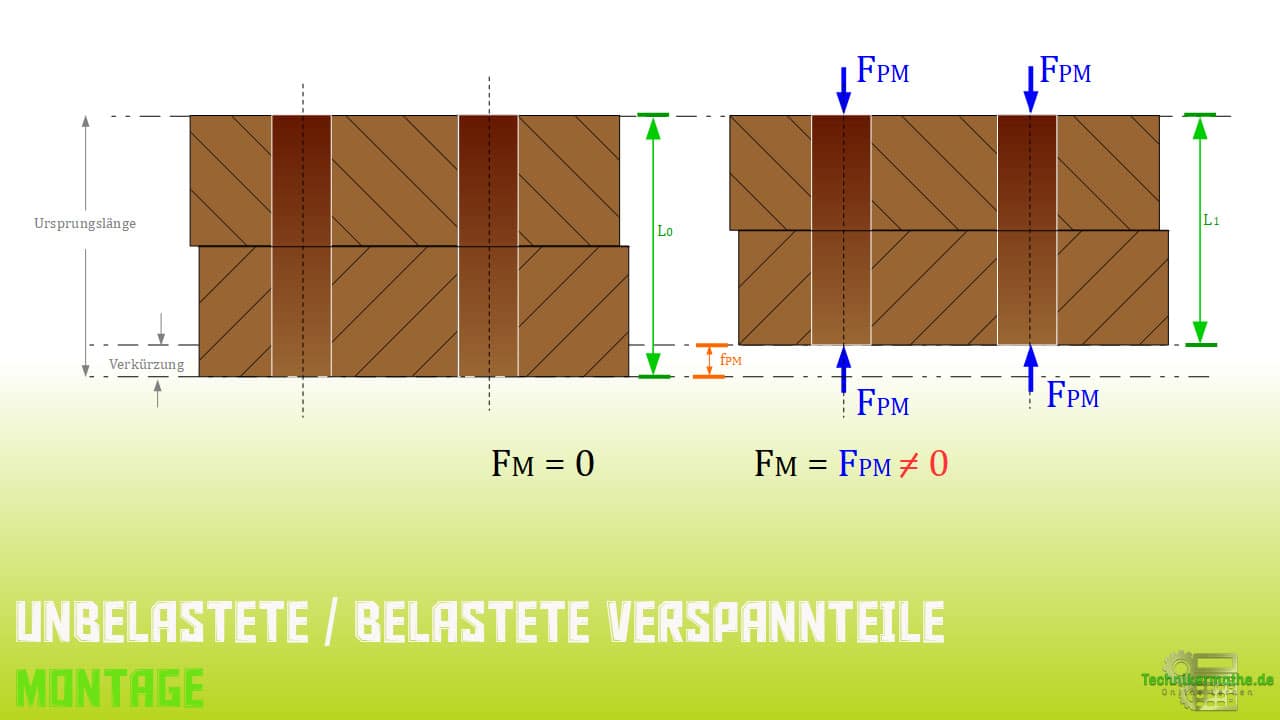
Montagezustand - Belastete und unbelastete Verspannteile — Montagezustand – Belastete und unbelastete Verspannteile

Die beiden abzulesenden Größen sind die Montagekraft der verspannten Teile $F_{PM}$ [P = verspannte Teile] und die Längenänderung der Teile $f_{PM}$ durch Stauchung.

Kräftegleichgewicht im Montagezustand

Bringen wir nun beide, also Schraube und verspannte Teile, zusammen, so zeigt sich, dass sich ein Gleichgewicht zwischen den jeweiligen Montagekräften einstellt im Montagezustand.

Formal sieht das dann wir folgt aus:

$F_M = F_{SM} = F_{PM}$

Kennzahlen:

$F_M =$ Montagekraft

$F_{SM} =$ Montagekraft der Schraube

$F_{PM} =$ Montagekraft der verspannten Teile.

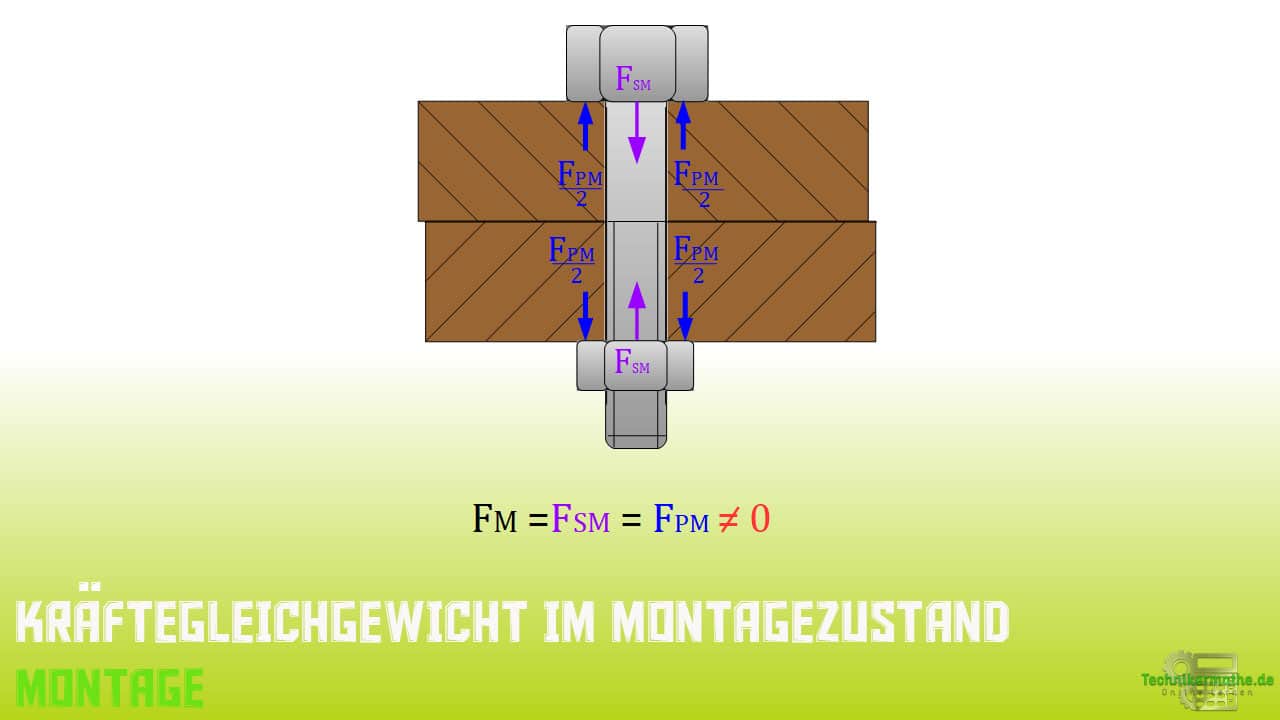
Den gleichen Effekt sehen wir in Hinblick auf die jeweilige Längenänderung. Denn die Längenänderung der Schraube ist betragsmäßig gleich mit der Längenänderung der verspannten Teile.

Formal sieht das dann wie folgt aus:

$|f| = f_{SM} = - f_{PM}$

Kennzahlen

$f =$ Längenänderung

$f_{SM} =$ Längenänderung infolge der Dehnung der Schraube

$f_{PM} =$ Längenänderung infolge der Stauchung der verspannten Teile

Kraft-Verlängerungs-Kurve

Um das Verhältnis zwischen wirkender Kraft $F$ und Längenänderung $f$ besser darstellen zu können, nutzen wir die im Maschinenbau gebräuchliche Kraft-Verlängerungs-Kurve.

Nicht selten wird diese Darstellung im auch Verspannungsschaubild genannt.

Kraft-Verlängerungskurve - Verspannungsschaubild — Kraft-Verlängerungskurve – Verspannungsschaubild

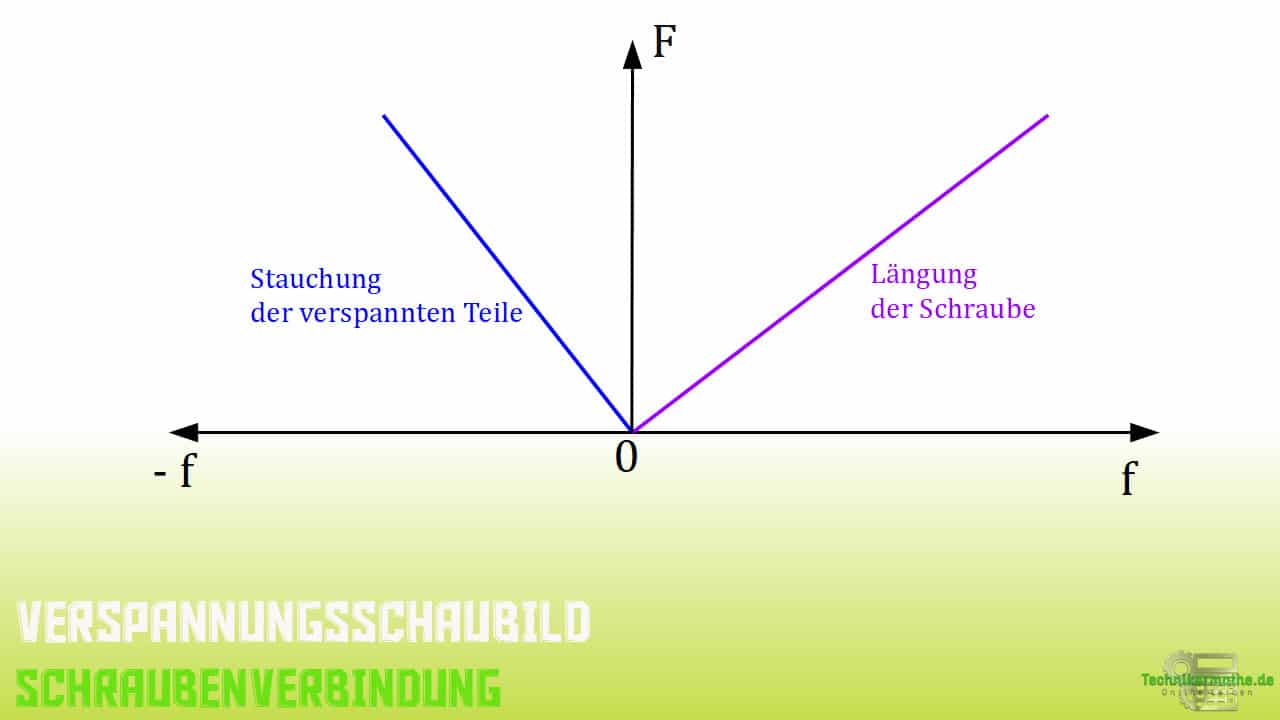
Auf der x-Achse wird die Längenänderung und auf der y-Achse die Kraft abgetragen. Da bei der Schraube eine Dehnung auftritt, wird der Zusammenhang zwischen Kraft und Verlängerung im rechten Quadranten (also positiv) als Kurve dargestellt. Im Fall von den gestauchten Teilen hingegen wird der Zusammenhang zwischen Kraft und Stauchung im linken Quadranten (also negativ) dargestellt.

Trotz der unterschiedlichen Steigungen der Kurven mit den Winkel $\alpha$ und $\beta$ , haben beide gemein, dass die Kurvenverläufe linear elastisch sind.

Winkel der Geraden im Verspannungsschaubild

Gerade der Schraube und Gerade der verspannten Teile

Zur Berechnung der jeweiligen Winkel der Geraden, ziehen wir die zuvor ermittelten Werte für die Nachgiebigkeiten von Schraube und verspannten Teile heran und können daraus zwei Gleichungen formulieren.

$tan \alpha = \frac{1}{\delta_S}$

Kennzahlen

$\alpha =$ Steigungswinkel der Kraft-Verlängerungs-Kurve der Schraube

$\delta_S =$ Nachgiebigkeit der Schraube

$tan \beta = \frac{1}{\delta_P}$

Kennzahlen

$\beta =$ Steigungswinkel der Kraft-Verlängerungs-Kurve der verspannten Teile

$\delta_P =$ Nachgiebigkeit der verspannten Teile

Ablesen von Werten aus dem Verspannungsschaubild

Mit Hilfe der Geraden von Schraube und Verspannungsteilen ist es nun möglich jedem Wert der Montagekraft den passenden Wert der Längenänderung zuzuordnen.

Vorgehensweise:

Schauen wir uns noch ein Mal das Verspannungsschaubild an und suchen uns einen Punkt auf der y-Achse. Diese Achse wird auch als Kraftachse bezeichnet.

Haben wir den richtigen Wert für unsere Montagekraft $F_M$ markiert, so können wir eine horizontale Linie (grau gestrichelt) ziehen, die sowohl die Gerade der Schraube als auch die Gerade der verspannten Teile schneidet.

Stauchung und Längung im Verspannungsschaubild

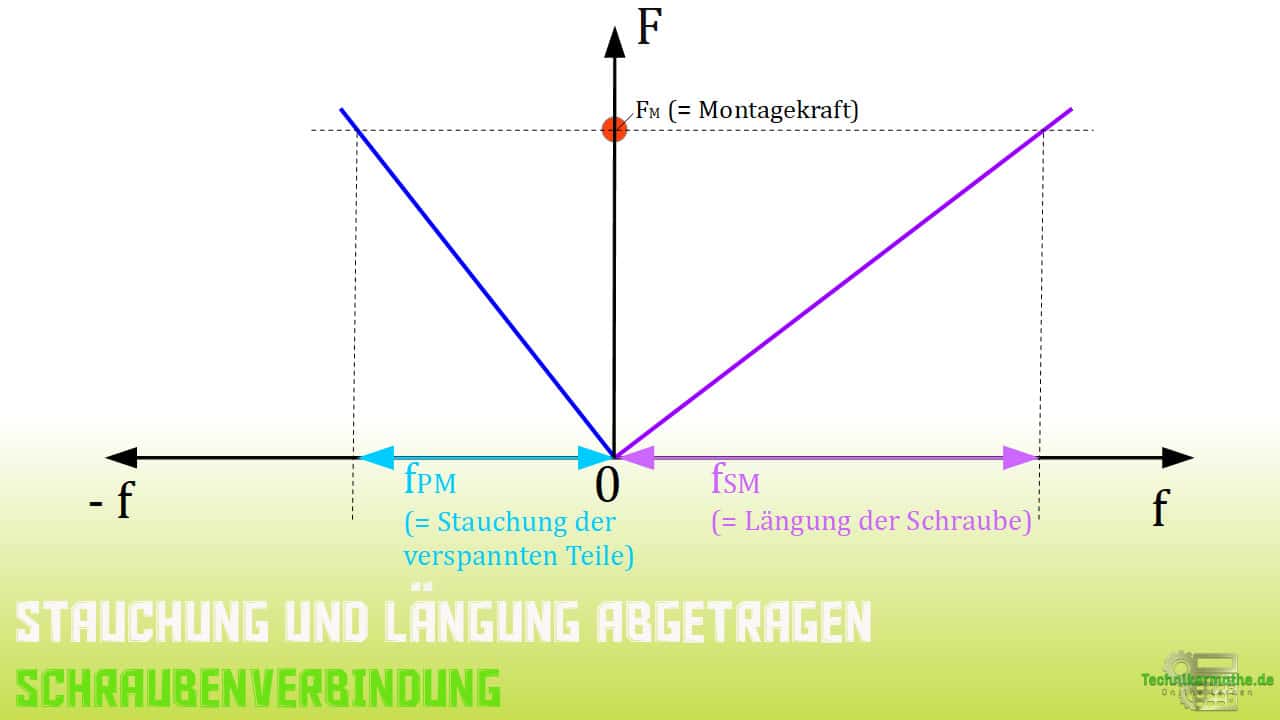
Der Schnittpunkt beider Gerade stellt den Wert der Längenänderung (Abstand zwischen Achsenursprung und Schnittpunkt) dar. Zum genauen Ablesen der Werte ziehen wir nun ausgehend von den Schnittpunkten zwei vertikale Geraden (grau gestrichelt), die die Y-Achse schneiden.

In den neuen Schnittpunkten können wir die Werte für die Längenänderung $f_{SM}$ und $f_{PM}$ genau ablesen.

Anpassung des Verspannungsschaubildes

Da bisher noch keine direkte Verbindung zwischen den beiden Gerade von Schraube und verspannten Teilen besteht, bedient man sich im Maschinenbau einer horizontalen Verschiebung.

In unserem Fall verschieben wir die Gerade der verspannten Teile so lange horizontal, bis diese sich auf Höhe der eingezeichneten Montagekraft in einem Punkt schneiden.

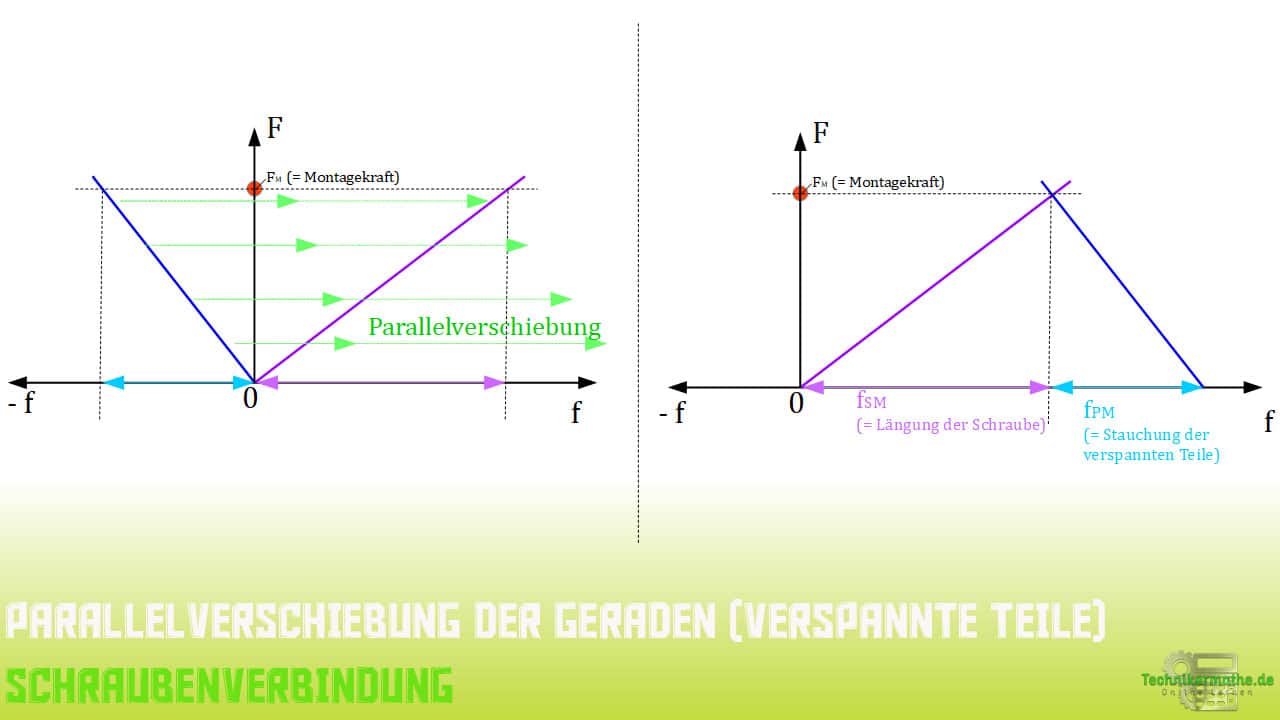
Erst jetzt haben wir eine vollständige Darstellung des Montagezustandes im Verspannungsschaubild.

Änderung der Montagekraft

Ändert sich die Montagekraft so ändert sich auch der Zusammenhang der beiden Geraden. Hier ist jedoch genau darauf zu achten, dass sich die beiden Winkel von $\alpha$ und $\beta$ nicht ändern.

Erhöhung der Montagekraft

Wird die Montagekraft $F_M$ erhöht, so muss die Gerade der verspannten Teile parallel nach rechts verschoben werden.

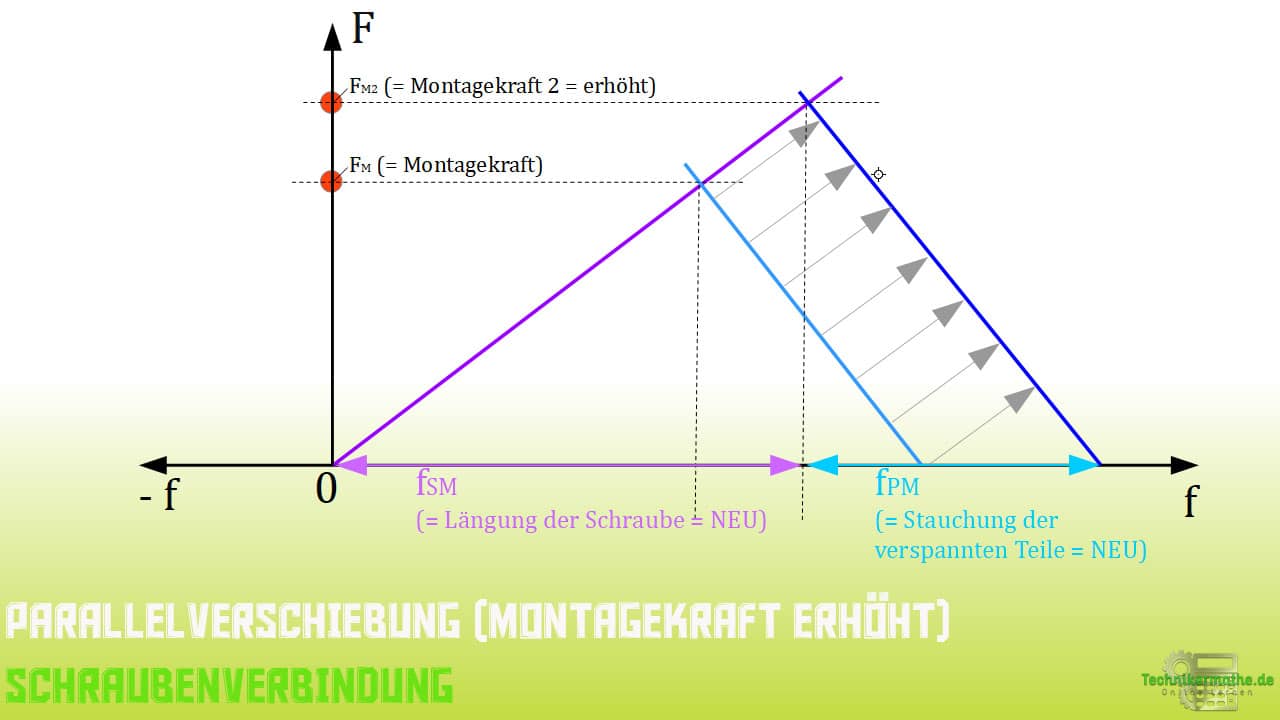
Änderung der Montagekraft - Verspannungsschaubild — Änderung der Montagekraft – Verspannungsschaubild

Die Verschiebung erfolgt so lange bis sich, die horizontale Linie (neue Linie = neue Montagekraft) sowie Gerade der Schraube und Gerade der verspannten Teile wieder in einem Punkt schneiden.

Verringerung der Montagekraft

Wird die Montagekraft $F_M$ verringert, so muss die Gerade der verspannten Teile parallel nach links verschoben werden.

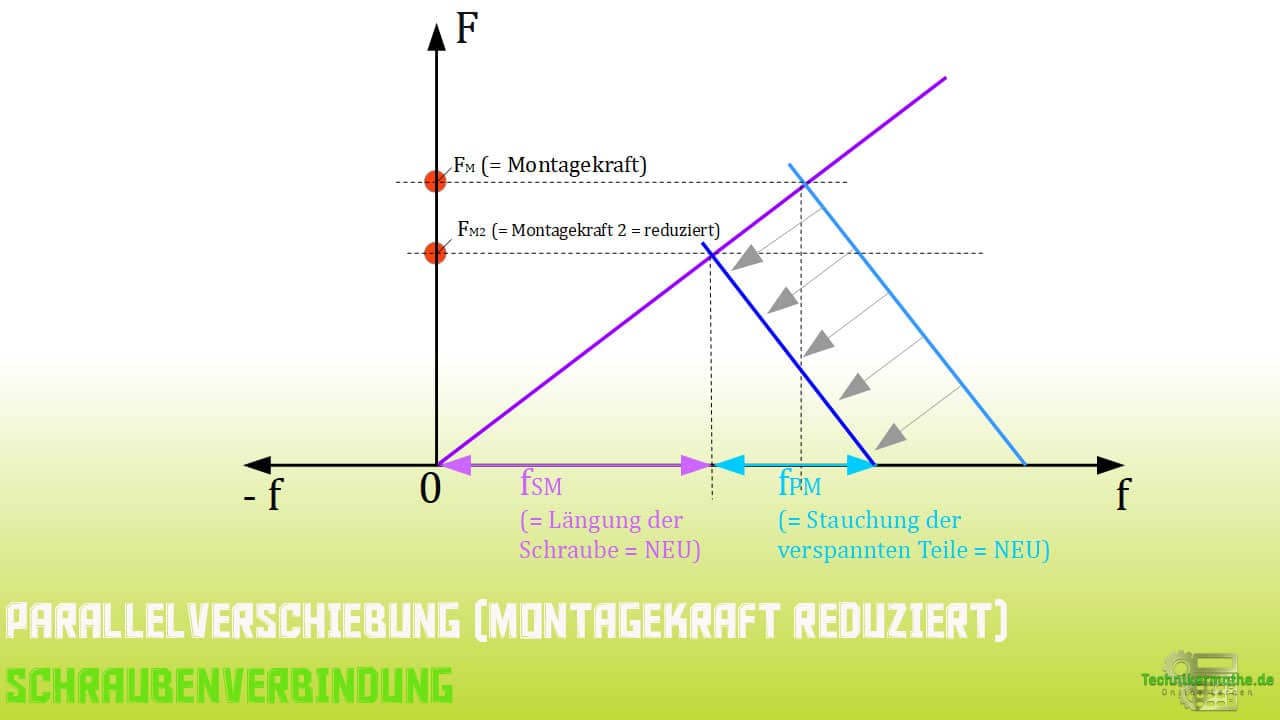
Auch hier erfolgt die Parallelverschiebung so lange bis sich die horizontale Linie (neue Linie = neue Montagekraft) sowie Gerade der Schraube und Gerade der verspannten Teile erneut in einem Punkt schneiden.

Neue Werte der Längenänderung

Unabhängig davon ob nun die Montagekraft erhöht oder reduziert wird, ergeben sich in beiden Fällen neue Werte für $f_{SM}$ und $f_{PM}$ . Auf der y-Achse teilen sich die Werte der Längenänderung durch die vertikale Linie zwischen Schnittpunkt der Geraden und Schnittpunkt der Linie mit der y-Achse auf.

Das Anzugsmoment

Das Anzugsmoment $M_A$ erzeugt die eigentliche Schraubenverbindung. Als zugehörigen Wert erhalten wir daraus die Vorspannkraft $F_M$ .

Aufgebracht wird das Anzugsmoment entweder über den Schraubenkopf (Schraube) oder die Mutter.

Die Methoden, die dabei angewandt werden, sind:

Anziehen per Hand
Anziehen durch manuellen Drehmomentschlüssel
Anziehen durch maschinellen Drehmomentschlüssel

Unabhängig von der verwendeten Methode, gilt, dass das Anzugsmoment ausreichend stark ausfallen muss, um eine notwendige Vorspannung zu erreichen und gleichzeitig auch die auftretenden Reibungen zwischen

Schraubenkopf und Bauteiloberfläche (Kopfreibungsmoment $M_K$ )

sowie

Schraubengewinde und Gegengewinde [ = Innengewinde im Bauteil / Innengewinde der Mutter] (Gewindereibungsmoment $M_G$ )

zu überwinden.

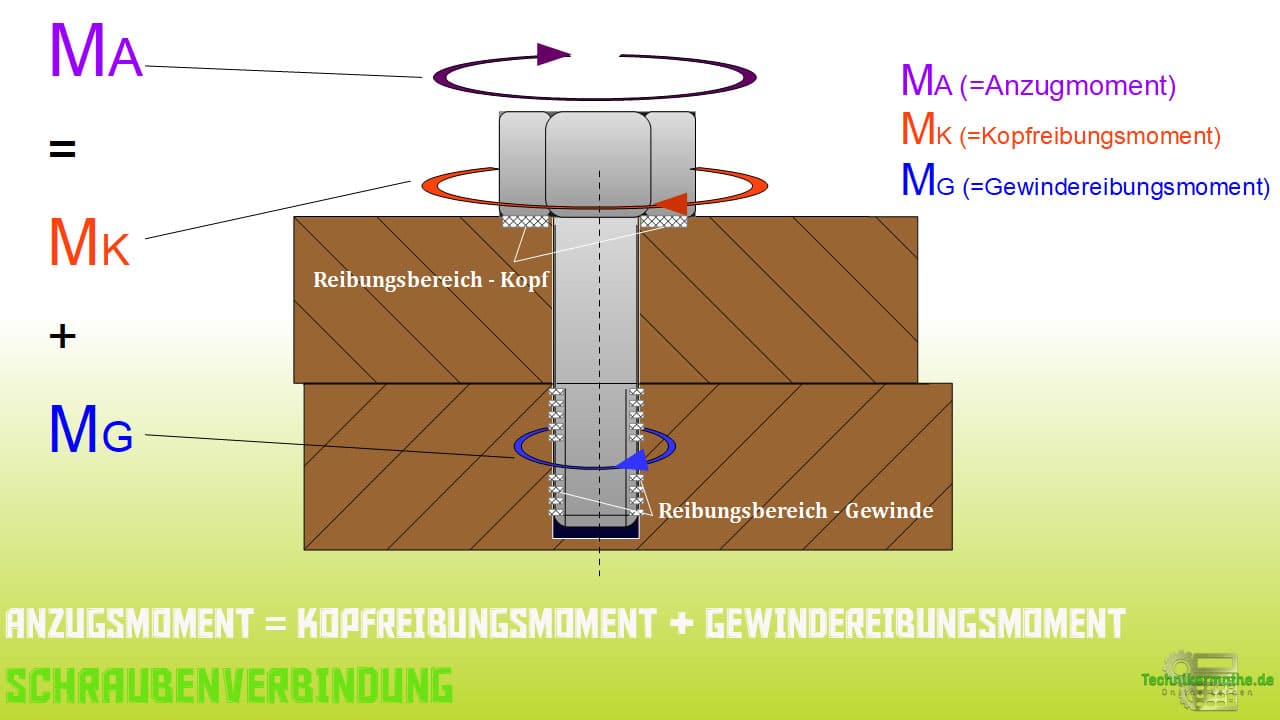
MERKE ! Aus langjähriger Erfahrung weiß man heute, dass ca. 90 % des Anzugsmoments für die Überwindung der Haftreibung und lediglich 10 % des Anzugsmoment für die Einstellung der erforderlichen Klemmkraft (axial) aufgewendet werden müssen.

In einer Berechnung des notwendigen Anzugsmoments unterscheiden wir zwischen den Anteilen von $M_K$ und $M_G$ .

Formal sieht das dann wie folgt aus:

$M_A = M_K + M_G$

Kennzahlen

$M_A =$ Anzugmoment

$M_K =$ Kopfreibungsmoment

$M_G =$ Gewindereibungsmoment

Die einzelnen Reibungsmomente werden, wie folgt ermittelt:

Kopfreibungsmoment

$M_K = F_M \cdot \frac{D_{KM}}{2} \cdot \mu_K$

Kennzahlen

$M_K =$ Kopfreibungsmoment

$F_M =$ Vorspannkraft

$D_{KM} =$ Mittlerer Kopfdurchmesser

$\mu_K =$ Reibwert zwischen Schraubenkopf und Bauteiloberfläche

Gewindereibungsmoment

$M_G = F_M \cdot \frac{d_2}{2} \cdot (tan \rho + tan \Phi)$

Kennzahlen

$M_G =$ Gewindereibungsmoment

$F_M =$ Vorspannkraft

$d_2 =$ Flankendurchmesser des Gewindes

$\rho =$ Reibungswertwinkel

$\Phi =$ Steigungswinkel

Der Wert für $tan \rho$ kann über die nachfolgende Gleichung ermittelt werden:

$tan \rho = \mu_G \cdot \frac{\alpha}{2}$

Kennzahlen

$\rho =$ Reibungswertwinkel

$\mu_G =$ Reibwert des Gewindes

$\alpha =$ Flankenwinkel

Beeinflussung der Reibwerte

Die Reibwerte des Schraubenkopfes $\mu_K$ und des Gewindes $\mu_G$ können durch technische und materialspezifische Maßnahmen beeinflusst werden. Dazu zählen

Herstellungsverfahren von Kopf und Gewinde,
Auswahl der Werkstoffe von Schraube und Mutter,
Wahl des eingesetzten Schmiermittels (Fette, Öl),
Oberflächenrauigkeit der eingesetzten Werkstoffe,

Darstellung der Reibwerte für unterschiedliche Montagezustände

Jetzt schauen wir uns noch einmal an, wie sich die Reibwerte von Schraubenkopf $\mu_K$ und Gewinde $\mu_G$ in einen bildlichen Zusammenhang mit der Montagekraft $F_M$ und dem Anzugsmoment $M_A$ bringen lassen.

In der ersten Abbildung sehen wir den Zusammenhang zwischen der Montagekraft $F_M$ und dem Reibwert des Gewindes $\mu_G$

In der zweiten Abbildung sehen wir den Zusammenhang zwischen Anzugsmoment $M_A$ und den unterschiedlichen Reibwerten des Gewindes $\mu_G$ , jetzt zudem ergänzt um die Kurve, die sich aus dem Zusammenhang von $\mu_G = \mu_K$ für unterschiedliche $\mu_G$ ergibt.

Typische Reibwerte für $\mu_G = \mu_K$ liegen zwischen $0,08 - 0,20$

Die Reibwerte können durch den Einsatz eines Klebstoffes nochmals erhöht werden.

Hier liegen die Reibwerte für $\mu_G = \mu_K$ zwischen $0,14 - 0,27$

Erzeugung eines notwendigen Drehmoments

Wie wir ja bereits wissen, müssen wir um den richtigen Montagezustand der Schraubenverbindung zu erreichen ein Drehmoment erzeugen. Dies gelingt uns indem wir die Schraube anziehen und dadurch gleichzeitig Vorspannkräfte erzeugen.

Um den gewünschten Montagezustand mit den zugehörigen Werten einzustellen, können wir uns mehr oder weniger guten Methoden bedienen.

Manuelle Drehmomenterzeugung

Die Fachkraft erzeugt das Drehmoment für den Montagezustand mit einem passenden Ringschlüssel, der entweder am Schraubenkopf oder der Mutter angreift. In beiden Fällen ist das allein durch Muskelkraft und Gefühl erzeugte Moment nicht ausreichend.

Die Streuung um das gewünschte Drehmoment herum liegt bei knapp 50 %. – Ungenügend!

Maschinelle Drehmomenterzeugung

Hier wird das Drehmoment maschinell erzeugt. Zur genauen Ermittlung des Drehmoments und die richtige Einstellung des Montagezustandes kann über verschiedene Methoden erreicht werden.

So lässt sich das notwendige Drehmoment mit Hilfe einer Verlängerungsmessung und einer Drehmomentmessung ermitteln.

Verlängerungsmessung: Anhaltspunkte sind die elastische Längenänderung und der Steigungswinkel des Gewindes.
Drehmomentmessung: Über die Widerstandsmessung am Drehmomentschlüssel kann das Drehmoment gemessen werden.

Weitere Methoden zur Einstellung des notwendigen Drehmoments

Erwärmung der Schraube

Eine praktische und sehr verbreitete Variante zur Erzeugung des richtigen Drehmoments ist die Erwärmung der Schraube.

Speziell große Schrauben werden mit dieser Methode, die komplett auf die Berücksichtigung von Reibungswerten verzichten kann, montiert.

Dabei wird die Schraube vor der Verschraubung in einem Ölbad oder einem niedrigtemperierten Ofen auf oberhalb von 90°C erwärmt. Dabei dehnt sich die Schraube minimal aus.

In diesem erwärmten Zustand verschraubt man die Schraube mit der Mutter bis alle Bestandteile direkt aneinander liegen. Infolge der Abkühlung zieht sich die Schraube wieder zusammen und wir erhalten die gewünschte Verspannung.

Obwohl diese Montageart eher brachial daherkommt, liegt die Streuung hier nur bei knapp 5 % um das gewünschte Drehmoment herum.

Motorisches Anziehen

Das motorische Anziehen erfolgt entweder mit einem Drehschrauber oder mit einem Schlagschrauber.

Drehschrauber nutzen ein kontinuierliches Drehmoment = Hohe Reibungsempflindlichkeit

Schlagschrauber verwenden Drehimpulse = Reduzierte Reibungsempflindlichkeit.

Bewertung der Verfahren

Oft ist es gewünscht, dass die einzelnen Verfahren über Vergleiche miteinander bewertet werden.

Hierzu eignen sich zwei Größen: Anziehfaktor $\alpha_A$ (in °) und die Streuung um das gewünschte Drehmoment (in % ).

Anziehfaktor

Der Anziehfaktor ist eine Verhältniszahl bestehend aus

Maximal zulässiger Montagekraft $F_{max}$

Minimal notwendiger Montagekraft $F_{min}$

$F_{max}$ darf dabei nicht überschritten werden, da es ansonsten zum Bruch der Schraube kommen kann.

$F_{min}$ darf nicht unterschritten werden, da es ansonsten zum Lockern der Schraubenverbindung kommen kann.

Formal sieht das dann wie folgt aus:

$\alpha_A = \frac{F_{max}}{F_{min}}$

Kennzahlen:

$\alpha_A =$ Anziehfaktor

$F_{max} =$ Maximale zulässige Montagekraft

$F_{min} =$ Minimal notwendige Montagekraft

In der nachfolgenden Abbildung sind die Verfahren in Bezug auf die beiden Größen tabellarisch aufgeführt.

Wie geht es weiter?...

Nachdem wir jetzt wissen, welche Berechnungen uns im Montagezustand einer Schraubenverbindung begegnen können, führen wir im nächsten Schritt die Untersuchung der Schraubenverbindung im Betriebszustand durch.

Was gibt es noch bei uns?

Finde die richtige Schule für dich!

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe.de?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Interaktive Übungsaufgaben

Übungsbereich

Demo–Quizfrage 1

Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?

Auszüge aus unserem Kursangebot

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
ET1 (Grundlagen der Elektrotechnik) und
ET2 (Gleichstromtechnik) an.

Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++